Question
Topic:
Discuss: Which diagram represents a heterogeneous mixture?
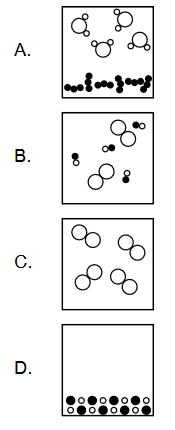
▶️Answer/Explanation
Ans:A
Solution:
A heterogeneous mixture is a mixture that is not uniform throughout, meaning that its components are not evenly distributed and can be visually distinguished. Examples of heterogeneous mixtures include mixtures of sand and water, oil and vinegar, or soil and gravel.
In terms of diagrams, a heterogeneous mixture can be represented by a diagram that shows distinct regions or phases of different components that are visibly separated. For example, a diagram of a mixture of oil and water would show two separate layers with the oil floating on top of the water. Another example would be a diagram of a mixture of sand and water, where the sand particles would settle at the bottom of the container, while the water would remain at the top.
Question
Topic:
Calculate: volume of carbon dioxide, $\mathrm{CO}_2(\mathrm{~g})$, can be obtained by reacting $1 \mathrm{dm}^3$ of methane, $\mathrm{CH}_4(\mathrm{~g})$, with $1 \mathrm{dm}^3$ of oxygen, $\mathrm{O}_2(\mathrm{~g})$ ?
$$
\mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(\mathrm{l})
$$
A. $0.5 \mathrm{dm}^3$
B. $1 \mathrm{dm}^3$
C. $2 \mathrm{dm}^3$
D. $6 \mathrm{dm}^3$
▶️Answer/Explanation
Ans:A
Solution:
1. All species discussed are gases: So we can use gas volume directly for calculation.
2. Determine limiting reagent:
For $\mathrm{CH}_4, 1 / 1=1.0 \mathrm{dm}^3 \quad$ For $0_2, 1 / 2=0.5 \mathrm{dm}^3$
Hence, $\mathrm{O}_2$ is the limiting reagent
3. Based on limiting reagent, determine volume of $\mathrm{CO}_2$
V\left(\mathrm{CO}_2\right)=\frac{1}{2} V\left(\mathrm{O}_2\right)=0.5 \mathrm{dm}^3
$$
Question
Topic:
Discuss: the empirical formula of a hydrocarbon with $75 \%$ carbon and $25 \%$ hydrogen by mass?
A. $\mathrm{C}_3 \mathrm{H}$
B. $\mathrm{CH}_2$
C. $\mathrm{C}_2 \mathrm{H}_6$
D. $\mathrm{CH}_4$
▶️Answer/Explanation
Ans:D
Solution:
To determine the empirical formula, we need to find the simplest whole number ratio of atoms in the compound.
Given that the compound has $75 \%$ carbon and $25 \%$ hydrogen by mass, we can assume that we have $75 \mathrm{g}$ of carbon and $25 \mathrm{g}$ of hydrogen in a $100 \mathrm{g}$ sample of the compound.
Next, we need to convert the masses of carbon and hydrogen to moles by dividing by their respective atomic masses:
Number of moles of $\mathrm{C} = \frac{75 \mathrm{g}}{12 \mathrm{g/mol}} = 6.25 \mathrm{mol}$
Number of moles of $\mathrm{H} = \frac{25 \mathrm{g}}{1 \mathrm{g/mol}} = 25 \mathrm{mol}$
Now we need to find the simplest whole number ratio of carbon to hydrogen. To do this, we can divide both the number of moles of carbon and hydrogen by the smallest number of moles:
Divide both sides by $6.25 \mathrm{mol}$:
Number of moles of $\mathrm{C} = 1$
Number of moles of $\mathrm{H} = \frac{25 \mathrm{mol}}{6.25 \mathrm{mol}} = 4$
So the empirical formula of the compound is $\mathrm{CH}_4$. Therefore, the answer is D.
Question
Topic:
Discuss: Which graph would not show a linear relationship for a fixed mass of an ideal gas with all other variables constant?
A. $\mathrm{P}$ against $\mathrm{V}$
B. $\mathrm{P}$ against $\frac{1}{\mathrm{V}}$
C. $\mathrm{P}$ against $\mathrm{T}$
D. $\mathrm{V}$ against $\mathrm{T}$
▶️Answer/Explanation
Ans:A
Solution:
For a fixed mass of an ideal gas with all other variables constant, the relationship between pressure ($\mathrm{P}$), volume ($\mathrm{V}$), and temperature ($\mathrm{T}$) is described by the ideal gas law:
$$\mathrm{PV} = \mathrm{nRT}$$
where $\mathrm{n}$ is the number of moles of gas and $\mathrm{R}$ is the universal gas constant.
Rearranging this equation gives:
$$\mathrm{P} = \frac{\mathrm{nRT}}{\mathrm{V}}$$
or
$$\mathrm{P} \mathrm{V} = \mathrm{nRT}$$
So, we can see that $\mathrm{P}$ is inversely proportional to $\mathrm{V}$, which means that the graph of $\mathrm{P}$ against $\frac{1}{\mathrm{V}}$ would show a linear relationship (Option B).
Similarly, we can use the ideal gas law to show that, for a fixed mass of an ideal gas with all other variables constant:
- $\mathrm{P}$ is directly proportional to $\mathrm{T}$ (Option C).
- $\mathrm{V}$ is directly proportional to $\mathrm{T}$ (Option D).
Therefore, the graph of $\mathrm{P}$ against $\mathrm{V}$ would not show a linear relationship (Option A). Instead, it would be a curve that follows the inverse relationship between $\mathrm{P}$ and $\mathrm{V}$ described by the ideal gas law.
Question
Topic:
Discuss: Bromine consists of two stable isotopes that exist in approximately a $1: 1$ ratio. The relative atomic mass, $A_r$, of bromine is 79.90 . Which are the stable isotopes of bromine?
A. ${ }^{79} \mathrm{Br}$ and ${ }^{81} \mathrm{Br}$
B. ${ }^{80} \mathrm{Br}$ and ${ }^{81} \mathrm{Br}$
C. ${ }^{78} \mathrm{Br}$ and ${ }^{80} \mathrm{Br}$
D. ${ }^{79} \mathrm{Br}$ and ${ }^{80} \mathrm{Br}$
▶️Answer/Explanation
Ans:A
Solution:
The relative atomic mass, $A_r$, of bromine is the weighted average of the masses of all its isotopes, taking into account their relative abundances. If bromine consists of two stable isotopes that exist in approximately a $1:1$ ratio, then we can assume that their masses are close to each other and their relative abundances are also close to $1/2$.
We can set up the following equation to solve for the atomic masses of the two isotopes:
$$A_r = (\text{fractional abundance of isotope 1}) \times (\text{atomic mass of isotope 1}) + (\text{fractional abundance of isotope 2}) \times (\text{atomic mass of isotope 2})$$
Since the two isotopes have equal abundances, we can simplify the equation to:
$$79.90 = (1/2) \times (\text{atomic mass of isotope 1}) + (1/2) \times (\text{atomic mass of isotope 2})$$
We can rearrange this equation to solve for the atomic masses:
$$(\text{atomic mass of isotope 1}) + (\text{atomic mass of isotope 2}) = 2 \times 79.90 = 159.80$$
There are different pairs of atomic masses that add up to 159.80, but only one pair that consists of stable isotopes: ${ }^{79} \mathrm{Br}$ and ${ }^{81} \mathrm{Br}$. Therefore, the stable isotopes of bromine are ${ }^{79} \mathrm{Br}$ and ${ }^{81} \mathrm{Br}$, and the answer is (A).
