Question
Topic:
Given: $0.10 \mathrm{~mol}$ of hydrochloric acid is mixed with $0.10 \mathrm{~mol}$ of calcium carbonate.
$$
2 \mathrm{HCl}(\mathrm{aq})+\mathrm{CaCO}_3(\mathrm{~s}) \rightarrow \mathrm{CaCl}_2(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{CO}_2(\mathrm{~g})
$$
Discuss: Which is correct?
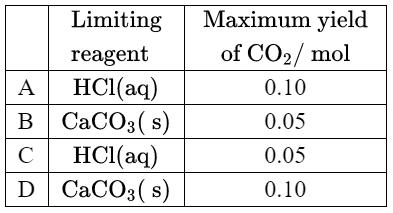
▶️Answer/Explanation
Ans:C
Solution:
To determine the limiting reagent, we can compare the number of moles of each reactant to the stoichiometric coefficients in the balanced chemical equation.
From the equation, we see that 2 moles of $\mathrm{HCl}$ react with 1 mole of $\mathrm{CaCO_3} to produce 1 mole of $\mathrm{CO_2}$. Therefore, the number of moles of $\mathrm{CO_2}$ that can be produced is limited by the reactant that is present in the lesser amount relative to its stoichiometric coefficient.
For $\mathrm{HCl}$: $\frac{0.10~\mathrm{mol}}{2} = 0.05~\mathrm{mol}$
For $\mathrm{CaCO_3}$: $\frac{0.10~\mathrm{mol}}{1} = 0.10~\mathrm{mol}$
Since $\mathrm{HCl}$ has a smaller value, it is the limiting reagent. Thus, the correct answer is option C.
To calculate the maximum yield of $\mathrm{CO_2}$, we use the amount of limiting reagent as the basis for our calculation. From the equation, we see that 1 mole of $\mathrm{CO_2}$ is produced for every 2 moles of $\mathrm{HCl}$ reacted. Therefore, the maximum yield of $\mathrm{CO_2}$ is:
$\mathrm{Maximum~yield~of~CO_2} = \frac{0.05~\mathrm{mol~HCl}}{2} = 0.025~\mathrm{mol}$
Therefore, the correct answer is also option C, with a maximum yield of 0.025 mol of $\mathrm{CO_2}$.
Question
Topic:
Calculate: the sum of the coefficients when the equation is balanced with whole numbers?
$$
\ldots{\mathrm{MnO}_2(\mathrm{~s})+\ldots} \mathrm{HCl}(\mathrm{aq}) \rightarrow\ldots\mathrm{MnCl}_2(\mathrm{aq})+\ldots \mathrm{H}_2 \mathrm{O}(\mathrm{l})+\ldots \mathrm{Cl}_2(\mathrm{~g})
$$
A. $6$
B. $7$
C. $8$
D. $9$
▶️Answer/Explanation
Ans:D
Solution:
First, let’s identify the unbalanced elements in the equation: $\mathrm{Mn, Cl, ~and~ H.}$
Next, we can begin balancing the equation by adding coefficients to the reactants and products to equalize the number of each type of atom on both sides of the equation.
$$
\mathrm{MnO}_2(\mathrm{s}) + 4\mathrm{HCl}(\mathrm{aq}) \rightarrow \mathrm{MnCl}_2(\mathrm{aq}) + 2\mathrm{H}_2\mathrm{O}(\mathrm{l}) + \mathrm{Cl}_2(\mathrm{g})
$$
Now the equation is balanced, and we can see that the sum of the coefficients is $1+4+1+2+1 = 9.$
Therefore, the correct answer is D, $9.$
Question
Topic:
Discuss: Which contains the greatest number of moles of oxygen atoms?
A. $ 0.05 \mathrm{~mol}~ \mathrm{Mg}\left(\mathrm{NO}_3\right)_2$
B. $0.05 \mathrm{~mol} ~\mathrm{C}_6 \mathrm{H}_4\left(\mathrm{NO}_2\right)_2$
C. $0.1 \mathrm{~mol} ~\mathrm{H}_2 \mathrm{O}$
D. $0.1 \mathrm{~mol}~ \mathrm{NO}_2$
▶️Answer/Explanation
Ans:A
Solution:
To determine the number of moles of oxygen atoms in each compound, we need to count the number of oxygen atoms in each formula and multiply by the number of moles given.
A. $0.05 \mathrm{~mol} \mathrm{Mg}\left(\mathrm{NO}_3\right)_2$ contains $2 \times 3 \times 0.05 = 0.3$ moles of oxygen atoms.
B. $0.05 \mathrm{~mol} \mathrm{C}_6 \mathrm{H}_4\left(\mathrm{NO}_2\right)_2$ contains $2 \times 2 \times 0.05 = 0.2$ moles of oxygen atoms.
C. $0.1 \mathrm{~mol} \mathrm{H}_2 \mathrm{O}$ contains $1 \times 0.1 = 0.1$ moles of oxygen atoms.
D. $0.1 \mathrm{~mol} \mathrm{NO}_2$ contains $2 \times 0.1 = 0.2$ moles of oxygen atoms.
Therefore, compound A contains the greatest number of moles of oxygen atoms, and the correct answer is A.
Question
Topic:
Discuss: Which represents the shape of an $\mathbf{s}$ atomic orbital?
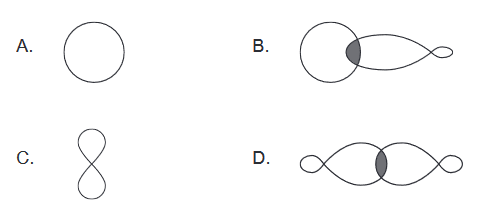
▶️Answer/Explanation
Ans:A
Solution:
An $\mathbf{s}$ atomic orbital has a spherical shape. It is characterized by a single lobe that surrounds the atomic nucleus, and the probability of finding an electron in the $\mathbf{s}$ orbital is highest at the nucleus and decreases as the distance from the nucleus increases.
Question
Topic:
Discuss: Which shows the first ionization energies of successive elements across period 2, from left to right?
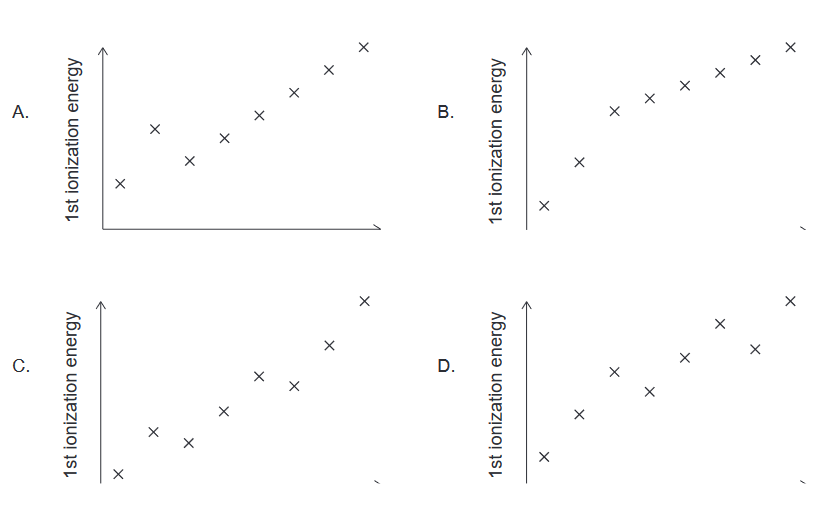
▶️Answer/Explanation
Ans:C
Solution:
$\mathrm{Li}$:$[\mathrm{He}] 2 s^1.$
$\mathrm{Be}$:$[\mathrm{He}] 2 s^2$
$\mathrm{B}$ :$[\mathrm{He}]2 s^2 2 p^1 \longrightarrow$ “shielding” from $2 s^2$
$\mathrm{C}$:$[\mathrm{He}]2 s^2 2 p^2$
$\mathrm{N}$ :$[\mathrm{He}]2 \mathrm{~s}^2 2 p^3$
$\mathrm{O}$ :$[\mathrm{He}]2 s^2 2 p^4 \rightarrow e^{-}-e^{-}$repulsion
$\mathrm{F}$:$[\mathrm{He}] 2 \mathrm{~s}^2 2 p^5$
$\mathrm{Ne}$:$[\mathrm{He}]2 s^2 2 p^6$

