Question-1 (a) :2021-nov-Chemistry_paper_2__TZ0_SL
Topic:
Given: A $4.406 \mathrm{~g}$ sample of a compound containing only $\mathrm{C}, \mathrm{H}$ and $\mathrm{O}$ was burnt in excess oxygen. $8.802 \mathrm{~g}$ of $\mathrm{CO}_2$ and $3.604 \mathrm{~g}$ of $\mathrm{H}_2 \mathrm{O}$ were produced.
Calculate: the empirical formula of the compound using section 6 of the data booklet.
Answer/Explanation
Solution:
We can calculate the empirical formula of the compound by using the masses of carbon, hydrogen, and oxygen in the sample. To do this, we first need to calculate the number of moles of carbon and hydrogen in the sample using the masses of $\mathrm{CO_2}$ and $\mathrm{H_2O}$ produced, as we did earlier:
$$n_{\mathrm{C}} = \frac{m_{\mathrm{CO_2}}}{M_{\mathrm{CO_2}}} = \frac{8.802~\mathrm{g}}{44.01~\mathrm{g/mol}} \approx 0.1998~\mathrm{mol}$$
$$n_{\mathrm{H}} = 2\times\frac{m_{\mathrm{H_2O}}}{M_{\mathrm{H_2O}}} = 2\times\frac{3.604~\mathrm{g}}{18.015~\mathrm{g/mol}} = 0.3998~\mathrm{mol}$$
Next, we can calculate the masses of carbon and hydrogen in the sample using their respective molar masses:
$$m_{\mathrm{C}} = n_{\mathrm{C}}\times M_{\mathrm{C}} = 0.1998~\mathrm{mol} \times 12.01~\mathrm{g/mol} = 2.401~\mathrm{g}$$
$$m_{\mathrm{H}} = n_{\mathrm{H}}\times M_{\mathrm{H}} = 0.3998~\mathrm{mol} \times 1.008~\mathrm{g/mol} = 0.402~\mathrm{g}$$
Finally, we can calculate the mass of oxygen in the sample by subtracting the masses of carbon and hydrogen from the total mass of the sample:
$$m_{\mathrm{O}} = m_{\mathrm{sample}} – m_{\mathrm{C}} – m_{\mathrm{H}} = 4.406~\mathrm{g} – 2.401~\mathrm{g} – 0.402~\mathrm{g} = 1.603~\mathrm{g}$$
Now we have the masses of carbon, hydrogen, and oxygen in the sample, and we can calculate the empirical formula of the compound by dividing each mass by its respective molar mass and then dividing by the smallest resulting value:
$$\begin{array}{c|ccc} \mathrm{Element} & \mathrm{C} & \mathrm{H} & \mathrm{O} \\ \hline \mathrm{Mass~(g)} & 2.401 & 0.402 & 1.603 \\ \mathrm{Molar~mass~(g/mol)} & 12.01 & 1.008 & 16.00 \\ \mathrm{Number~of~moles} & 0.1998 & 0.3998 & 0.1002 \\ \mathrm{Mole~ratio}\approx & 2 & 4 & 1 \end{array}$$
So the empirical formula of the compound is also $\mathrm{C_2H_4O}$.
Question-1 (b) :2021-nov-Chemistry_paper_2__TZ0_SL
Topic:
Calculate: the molecular formula of this compound if its molar mass is $88.12 \mathrm{~g} \mathrm{~mol}^{-1}$. If you did not obtain an answer in (a) use CS, but this is not the correct answer.
Answer/Explanation
Solution:
Since the empirical formula of the compound is $\mathrm{C}_2\mathrm{H}_4\mathrm{O}$ with a molar mass of $88.12~\mathrm{g~mol^{-1}}$, we can calculate the empirical formula mass as follows:
$\mathrm{C}_2\mathrm{H}_4\mathrm{O} = (2 \times 12.01) + (4 \times 1.01) + (16.00) = 44.06~\mathrm{g~mol^{-1}}$
To determine the molecular formula of the compound, we need to know how many times the empirical formula must be multiplied to get the molar mass of the actual compound. We can find this factor by dividing the molar mass of the actual compound by the empirical formula mass:
$\text{Factor} = \dfrac{88.12~\mathrm{g~mol^{-1}}}{44.06~\mathrm{g~mol^{-1}}} = 2$
This means that the molecular formula of the compound is twice the empirical formula, so we need to multiply the subscripts in the empirical formula by 2 to get the molecular formula:
$\mathrm{C}_2\mathrm{H}_4\mathrm{O} \times 2 = \mathrm{C}_4\mathrm{H}_8\mathrm{O}_2$
Therefore, the molecular formula of the compound is $\mathrm{C}_4\mathrm{H}_8\mathrm{O}_2$.
Question-1 (c) :2021-nov-Chemistry_paper_2__TZ0_SL
Topic:
Given: The following spectrums show the Infrared spectra of propan-1-ol, propanal and propanoic acid.
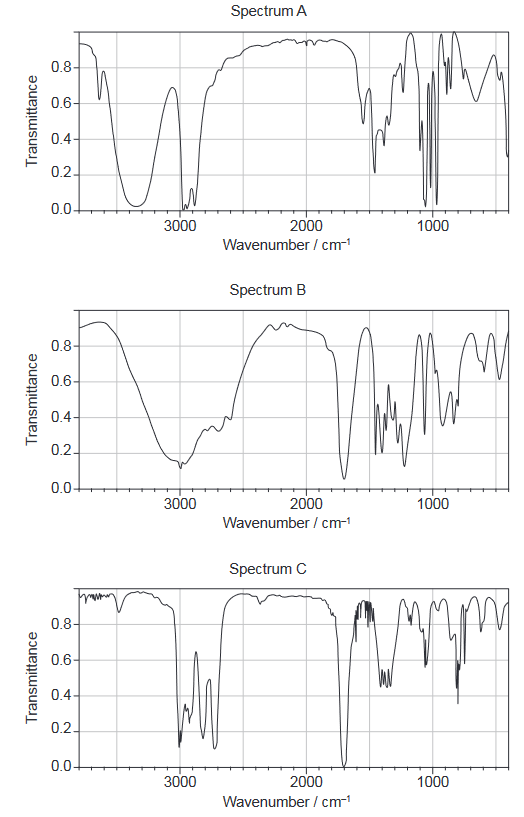
Discuss: each compound from the spectra given, use absorptions from the range of $1700 \mathrm{~cm}^{-1}$ to $3500 \mathrm{~cm}^{-1}$. Explain the reason for your choice, referring to section 26 of the data booklet.

Answer/Explanation
Solution:

Question-2 (a) :2021-nov-Chemistry_paper_2__TZ0_SL
Topic:
Given: Electron transitions are related to trends in the periodic table.
Explain: the general increase in trend in the first ionization energies of the period 3 elements, $\mathrm{Na}$ to $\mathrm{Ar}$.
Answer/Explanation
Solution:
The first ionization energy of an element is the energy required to remove one electron from the neutral atom in its gaseous state. In general, there is an increasing trend in the first ionization energies of the period 3 elements, $\mathrm{Na}$ to $\mathrm{Ar}$. This trend can be explained by the increasing effective nuclear charge experienced by the valence electrons as one moves from left to right across the period.
Effective nuclear charge is the net positive charge experienced by an electron in an atom. It is equal to the nuclear charge (the number of protons in the nucleus) minus the shielding effect of the inner electrons. As we move from left to right across period 3, the number of protons in the nucleus increases, but the number of inner electrons remains the same. This means that the effective nuclear charge experienced by the valence electrons increases, making it more difficult to remove them from the atom.
As a result, the first ionization energy of the period 3 elements increases from $\mathrm{Na}$ to $\mathrm{Ar}$. The trend is not perfectly regular, however, due to exceptions such as the lower ionization energy of $\mathrm{Mg}$ compared to $\mathrm{Be}$ and the lower ionization energy of $\mathrm{P}$ compared to $\mathrm{S}$. These exceptions can be explained by additional factors such as electron-electron repulsion and electron pairing.
Question-3 [(a) (i)] :2021-nov-Chemistry_paper_2__TZ0_SL
Topic:
Given: White phosphorus is an allotrope of phosphorus and exists as $\mathrm{P}_4$
Draw: the Lewis (electron dot) structure of the $\mathrm{P}_4$ molecule, containing only single bonds.
Answer/Explanation
Solution:
Here’s a sketch of the Lewis (electron dot) structure of $\mathrm{P}_4$:
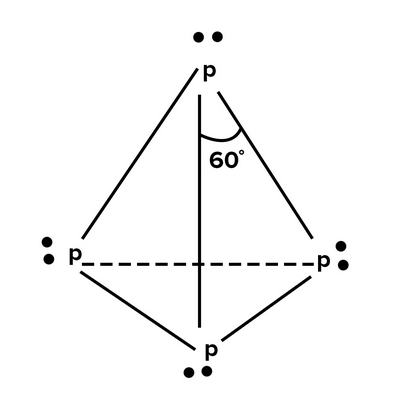
In this structure, each $\mathrm{P}$ atom has 5 valence electrons, and each atom is bonded to three other $\mathrm{P}$ atoms, with one lone pair on each atom. The bond angle in $\mathrm{P}_4$ is approximately 60 degrees, which is consistent with the sp3 hybridization of the $\mathrm{P}$ atoms in the molecule.
Note:
Tetrahedral molecules usually have bond angles of approximately 109.5 degrees. However, in the case of $\mathrm{P}_4$, the molecule is not perfectly tetrahedral due to the presence of lone pairs on each of the $\mathrm{P}$ atoms. These lone pairs cause repulsion and result in a slight compression of the bond angles, resulting in a bond angle of approximately 60 degrees. This is a common phenomenon in molecules with lone pairs, where the geometry is distorted from the ideal geometry due to the repulsive forces between the lone pairs and bonding pairs.
Question-3 [(a) (ii)] :2021-nov-Chemistry_paper_2__TZ0_SL
Topic:
Write : an equation for the reaction of white phosphorus $\left(\mathrm{P}_4\right)$ with chlorine gas to form phosphorus trichloride $\left(\mathrm{PCl}_3\right)$.
Answer/Explanation
Solution:
The equation for the reaction of white phosphorus with chlorine gas to form phosphorus trichloride is:
$\mathrm{P}_4 + 6\mathrm{Cl}_2 \rightarrow 4\mathrm{PCl}_3$
