Question-1 :2022-may-Chemistry_paper_1__TZ2_SL
Topic:
Discuss: What is the concentration of chloride ions, in $\mathrm{mol} \mathrm{dm}^{-3}$, in a solution formed by mixing $200 \mathrm{~cm}^3$ of $1 \mathrm{~mol} \mathrm{dm}^{-3} \mathrm{HCl}$ with $200 \mathrm{~cm}^3$ of $5 \mathrm{~mol} \mathrm{dm}^{-3} ~\mathrm{NaCl}$ ?
A. $1$
B. $2$
C. $3$
D. $6$
Answer/Explanation
Solution:
To determine the concentration of chloride ions in the solution, we first need to calculate the total number of moles of chloride ions present in the solution. We can do this by using the formula:
$$
\text { moles }=\text { concentration } \times \text { volume }
$$
For the hydrochloric acid solution:
$$\text{moles of chloride ions = concentration} \times \text{volume}$$
$$
\begin{aligned}
& =1 \mathrm{~mol} / \mathrm{dm}^3 \times(200 / 1000) d m^3 \\
& =0.2 \text { moles }
\end{aligned}
$$
For the sodium chloride solution:
$$\text{moles of chloride ions = concentration} \times \text{volume}$$
$$
\begin{aligned}
& =5 \mathrm{~mol} / \mathrm{dm}^3 \times(200 / 1000) \mathrm{dm}^3 \\
& =1 \mathrm{moles}
\end{aligned}
$$
The total number of moles of chloride ions in the solution is therefore:
$$
0.2 \text { moles }+1 \text { moles }=1.2 \text { moles }
$$
Finally, we can calculate the concentration of chloride ions in the solution by dividing the total number of moles by the total volume
$$\text{concentration}=\frac{ \text { moles }}{\text { Volume }}$$
$$
\begin{aligned}
& =\frac{1.2 ~\mathrm{moles}}{(200 / 1000+200 / 1000)\mathrm{dm}^3} \\
& =3 \mathrm{~mol} / \mathrm{dm}^3
\end{aligned}
$$
$\colorbox{yellow}{Correct Option : C }$
Question-2 :2022-may-Chemistry_paper_1__TZ2_SL
Topic:
Given: $30 \mathrm{~g}$ of an organic compound produces $44 \mathrm{~g} \mathrm{CO}_2$ and $18 \mathrm{~g} \mathrm{H}_2 \mathrm{O}$ as the only combustion products.
$$
M_{\mathrm{r}} \mathrm{CO}_2=44 \mathrm{M}_{\mathrm{r}} \mathrm{H}_2 \mathrm{O}=18
$$
Calculate: Which of the following is the empirical formula for this compound?
A. $\mathrm{CH}_2$
B. $\mathrm{CH}_3$
C. $\mathrm{CHO}$
D. $\mathrm{CH}_2 \mathrm{O}$
Answer/Explanation
Solution:
To determine the empirical formula of the organic compound, we need to find the ratio of the number of atoms of each element in the compound.
Let’s first find the number of moles of $\mathrm{CO}_2$ and $\mathrm{H}_2\mathrm{O}$ produced by the combustion of $30\mathrm{~g}$ of the compound.
The number of moles of $\mathrm{CO}_2$ is:
$$
\text { moles of } \mathrm{CO}_2=\frac{44 \mathrm{~g}}{44 \mathrm{~g} / \mathrm{mol}}=1 \mathrm{~mol}
$$
The number of moles of $\mathrm{H}_2\mathrm{O}$ is:
$$\text { moles of } \mathrm{H}_2 \mathrm{O}=\frac{18 \mathrm{~g}}{18 \mathrm{~g} / \mathrm{mol}}=1 \mathrm{~mol}$$
Next, we can find the number of moles of carbon and hydrogen in the compound using the balanced chemical equation for the combustion of the compound:
$$
\mathrm{C}_x \mathrm{H}_y+\frac{(x+2 y)}{4} \mathrm{O}_2 \rightarrow x \mathrm{CO}_2+\frac{y}{2} \mathrm{H}_2 \mathrm{O}
$$
From the equation, we can see that $1$ mole of the compound produces $x$ moles of $\mathrm{CO}_2$ and $y/2$ moles of $\mathrm{H}_2\mathrm{O}$. Therefore:
$$\begin{aligned} & x=\frac{1 \mathrm{~mol} \mathrm{CO}_2}{1 \mathrm{~mol} \text { of compound }}=1 \mathrm{~mol} \\ & y / 2=\frac{1 \mathrm{~mol} \mathrm{H}_2 \mathrm{O}}{1 \mathrm{~mol} \text { of compound }}=1 \mathrm{~mol}\end{aligned}$$
So, the empirical formula of the compound is $\mathrm{CH}_2\mathrm{O}$, which corresponds to a molecular mass of $30\mathrm{~g/mol}$.
$\colorbox{yellow}{$\mathrm{CH}_2\mathrm{O}$ (D)}$.
Question-3 :2022-may-Chemistry_paper_1__TZ2_SL
Topic:
Discuss: Which graph represents the relationship between the amount of gas, $\mathrm{n}$, and the absolute temperature, $\mathrm{T}$, with all other variables in the ideal gas equation, $P V=n R T$, held constant?
Answer/Explanation
Solution:
The ideal gas equation is given by $PV = nRT$, where $P$ is the pressure, $V$ is the volume, $n$ is the amount of gas in moles, $R$ is the gas constant, and $T$ is the absolute temperature.
If we hold the pressure, volume, and amount of gas constant, then the ideal gas equation becomes $T = \frac{PV}{nR}$. This means that the temperature is directly proportional to the product of pressure and volume, and inversely proportional to the amount of gas.
Therefore, if we plot $n$ on the x-axis and $T$ on the y-axis, with constant pressure and volume, we should see an inverse relationship between $n$ and $T$. This is because as the amount of gas decreases, the temperature must also decrease to maintain a constant pressure and volume.
So, the correct graph would be one where we see an inverse relationship between $n$ and $T$. Here is graph:
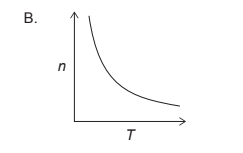
Question-4 :2022-may-Chemistry_paper_1__TZ2_SL
Topic:
Discuss: Which equation represents the deposition of iodine?
A. $\mathrm{I}_2(\mathrm{~g}) \rightarrow \mathrm{I}_2(\mathrm{l})$
B. $\mathrm{I}_2(\mathrm{~g}) \rightarrow \mathrm{I}_2(\mathrm{~s})$
C. $\mathrm{I}_2(\mathrm{l}) \rightarrow \mathrm{I}_2(\mathrm{~g})$
D. $\mathrm{I}_2(\mathrm{~s}) \rightarrow \mathrm{I}_2(\mathrm{~g})$
Answer/Explanation
Solution:
The correct equation that represents the deposition of iodine is $\colorbox{yellow}{option B: $\mathrm{I}_2(\mathrm{~g}) \rightarrow \mathrm{I}_2(\mathrm{~s})$}$. Deposition is the process of a substance changing from a gas directly to a solid without passing through the liquid phase. Therefore, the deposition of iodine occurs when iodine in the gaseous state directly changes to the solid state.
Question-5 :2022-may-Chemistry_paper_1__TZ2_SL
Topic:
Discuss: Which experimental results support the theory that electrons exist in discrete energy levels?
A. ${ }^1 \mathbf{H~NMR}$
B. X-ray diffraction pattern
C. Emission spectra
D. IR spectra
Answer/Explanation
Solution:
$\colorbox{yellow}{The experimental results that support the theory that electrons exist in discrete energy levels are emission spectra.}$
When an electron is excited to a higher energy level, it gains potential energy. When it returns to its original energy level, it releases the excess energy as a photon of light. The energy of the emitted photon corresponds to the energy difference between the two energy levels involved in the transition. This means that when the emitted light is passed through a prism or a diffraction grating, it produces a spectrum consisting of discrete lines at specific wavelengths. These wavelengths correspond to the energy differences between the energy levels of the electron.
The emission spectra provide direct evidence of the existence of discrete energy levels in atoms and molecules, and they were crucial in the development of the quantum theory of the atom. Therefore, option C is the correct answer. Options A, B, and D involve different experimental techniques and do not directly relate to the discrete energy levels of electrons.
