2022-Nov-Physics_paper_1__TZ0_HL – All Questions with detailed solution
Q.1.2022-Nov-Physics_paper_1__TZ0_HL
Topic: Forces
Discuss: The definition of the SI unit for a force
A. The force required to accelerate, in the direction of the force, a mass of $1 \mathrm{~kg}$ at $1 \mathrm{~ms}^{-2}$
B. The force required to accelerate, in the direction of the force, a mass at $1 \mathrm{~ms}^{-2}$
C. The weight of a mass of $0.1 \mathrm{~kg}$
D. The change in momentum per second
Answer/Explanation
Solution:
“The force required to accelerate, in the direction of the force, a mass of $1 \mathrm{~kg}$ at $1 \mathrm{~ms}^{-2}$”. This unit is called the Newton (N), and it is defined as the amount of force required to give a mass of $1 \mathrm{~kg}$ an acceleration of $1 \mathrm{~ms}^{-2}$ in the direction of the force. In other words, if a force of $1 \mathrm{~N}$ is applied to a mass of $1 \mathrm{~kg}$, it will accelerate at a rate of $1 \mathrm{~ms}^{-2}$. The Newton is named after Sir Isaac Newton, the English mathematician and physicist who first formulated the laws of motion.
Q.2.2022-Nov-Physics_paper_1__TZ0_HL
Topic: Uncertainties and errors
Given: Rectangular sheet of paper has dimensions of $(30.0 \pm 0.5) \mathrm{cm}$ and $(20.0 \pm 0.5) \mathrm{cm}$.
Calculate: What is the percentage uncertainty of the perimeter of the paper?
A. $1 \%$
B. $2 \%$
C. $2.5 \%$
D. $4 \%$
Answer/Explanation
Solution:
The perimeter $P$ of the rectangular sheet of paper is given by:
$P = 2(l+w)$
where $l$ and $w$ are the length and width of the rectangle, respectively.
Using the values given, we have:
$l = (30.0 \pm 0.5) \mathrm{cm}$$ $$w = (20.0 \pm 0.5) \mathrm{cm}$
So the perimeter is:
$P = 2[(30.0) \mathrm{cm} + (20.0 ) \mathrm{cm}]$
Simplifying:
$P = 2 \times 50.0 \mathrm{cm} = 100.0 \mathrm{cm}$
Therefore, the absolute uncertainty in the perimeter is:
$\Delta P = 2(\Delta \mathrm{0.5}+\Delta \mathrm{0.5})=2 \mathrm{cm}$
And the percentage uncertainty is:
$\frac{\Delta P}{P} \times 100\%=\frac{2.0 \mathrm{cm}}{100.0 \mathrm{cm}} \times 100\% = 2.0\%$
Therefore, the percentage uncertainty of the perimeter of the paper is $\boxed{2.0\%}$.
Q.3.2022-Nov-Physics_paper_1__TZ0_HL
Topic: Vectors and scalars
Given: Two forces, $\mathrm{F}$ and $\mathrm{G}$, act on a system.
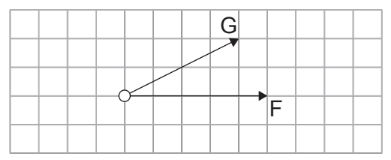Now, $\mathrm{F}$ is reversed in direction and $\mathrm{G}$ is halved.
Discuss: Which vector correctly represents the new resultant force?
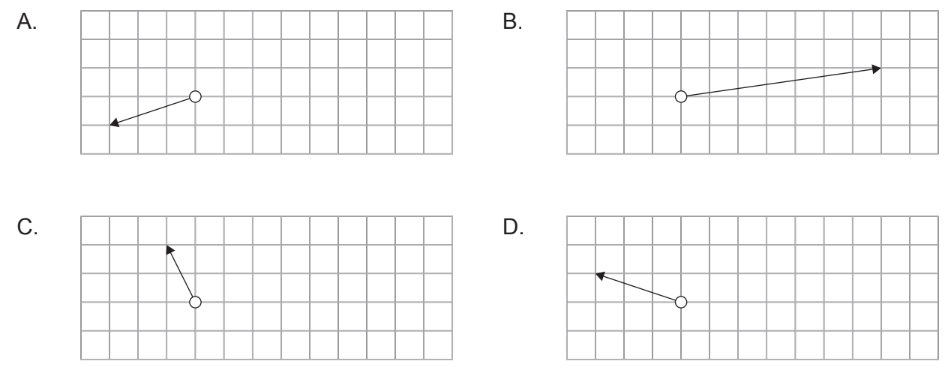
Answer/Explanation
Solution:
When the direction of $\mathrm{F}$ is reversed and the magnitude of $\mathrm{G}$ is halved.
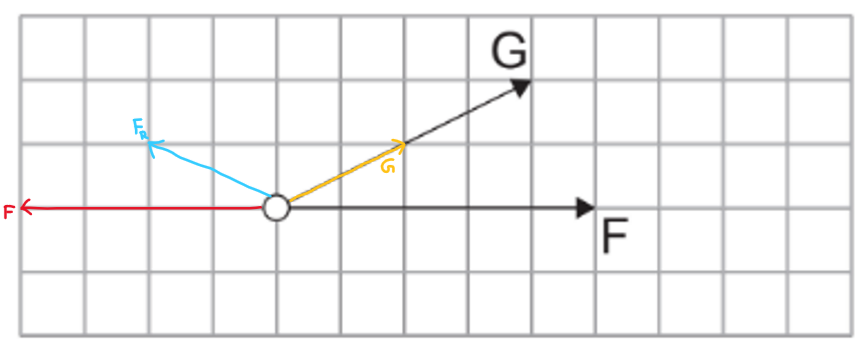
Q.4.2022-Nov-Physics_paper_1__TZ0_HL
Topic: Motion
Given: Ball 1 is dropped from rest from an initial height $h.$ At the same instant, ball 2 is launched vertically upwards at an initial velocity $u$.
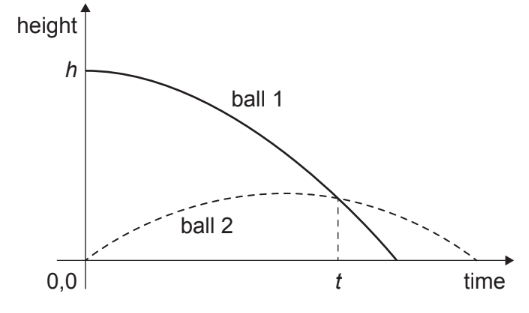
Calculate: At what time are both balls at the same distance above the ground?
A. $\frac{h}{4 u}$
B. $\frac{h}{2 u}$
C. $\frac{h}{u}$
D. $\frac{2 h}{u}$
Answer/Explanation
Solution:
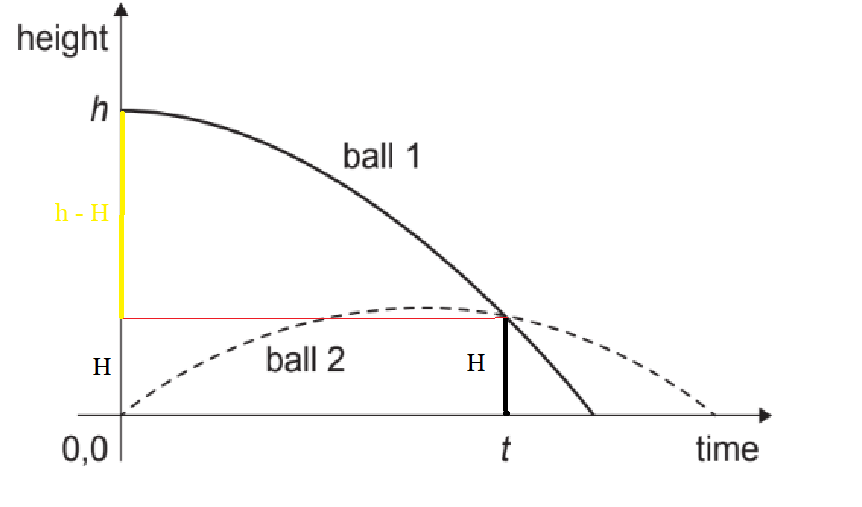
Let both balls meet at $\mathrm{H}$
Using equation of motion for ball 1 which is launched vertically up with velocity $u$,
\( H=u t-\frac{1}{2} gt^2\quad\text{[eq-1]} \)
Now, writing the eqaution of motion for ball 2 which is dropped ($u=0$) in this case,
\(h- H=\frac{1}{2} gt^2\quad\text{[eq-2]} \)
$\text{Adding eq-(1) and eq-(2)}$
$h=ut$
$t=\frac{h}{u}$
Q.5.2022-Nov-Physics_paper_1__TZ0_HL
Topic: Motion
Given: The diagram shows the trajectory of a projectile and the velocity v of the projectile at point P in its trajectory. P is located before the projectile reaches the peak altitude. Air resistance acts on the projectile. The acceleration of the projectile at$ P$ is a.
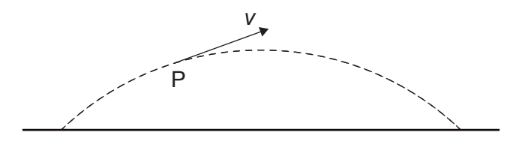
Discuss: What are the magnitudes of the horizontal component and the vertical component of the acceleration of the projectile at P?
Answer/Explanation
Solution:
Since the projectile is experiencing air resistance, the acceleration of the projectile is not constant. However, at any point in its trajectory, the acceleration of the projectile can be decomposed into two components: the horizontal component and the vertical component.
At point $P$, the projectile is not at its maximum height, and its velocity vector has both horizontal and vertical components. Therefore, the acceleration of the projectile at point $P$ has both horizontal and vertical components.
The horizontal component of the acceleration of the projectile is affected by air resistance, but it is constant. This is because there is no horizontal force acting on the projectile in the absence of air resistance, and air resistance only acts in the direction opposite to the horizontal velocity of the projectile. Therefore, the magnitude of the horizontal component of the acceleration of the projectile at point $P$ is $\boxed{\text{non-zero}}$
The vertical component of the acceleration of the projectile is affected by air resistance and gravity. Gravity acts downward with a magnitude of $9.8 \mathrm{~ms}^{-2}$, while air resistance acts in the direction opposite to the velocity vector of the projectile. The vertical component of the acceleration of the projectile at point $P$ is greater than $9.8 \mathrm{~ms}^{-2}$, since air resistance reduces the net force acting on the projectile in the vertical direction. Therefore, the magnitude of the vertical component of the acceleration of the projectile at point $P$ is $\boxed{\text{greater than } 9.8 \mathrm{~ms}^{-2}}$