2022-May-Physics_paper_1__TZ1_HL – All Questions with detailed solution
Q.1.2022-May-Physics_paper_1__TZ1_HL
Topic: Measurements in physics
Given: Intensity $=\frac{Energy}{Area\times t}$
Calculate: Exprese unit of intensity in fundamental SI units
A. $\mathrm{kg} \mathrm{m}^{-2} \mathrm{~s}^{-1}$
B. $\mathrm{kg} \mathrm{m}^2 \mathrm{~s}^{-3}$
C. $\mathrm{kg} \mathrm{s}^{-2}$
D. $\mathrm{kg} \mathrm{s}^{-3}$
Answer/Explanation
Solution:
As given ,
$
\text { Intensity }=\frac{\text { Energy }}{\text { Area } \times t} \Rightarrow \frac{\text { Power }}{\text { Area }}[\text { Energy/time }=\text { Power }]
$
$\text{Force=mass}\times \text{accelaration }=\mathrm{kg.ms}^{-2}$
$\text{Velocity =m/s}$
[$\text{Power= force} \times \text{velocity}$ ]
SI unit of Power $=\mathrm{kgm}^2 \mathrm{sec}^{-3}$
SI unit of Area $=m^2$
Q.2.2022-May-Physics_paper_1__TZ1_HL
Topic: Vector
Given: resultant of two forces acting on a body is 12 N
Calculate: Below pair of forces acting on the body can combine to produce 12 N?
A. $ 1 \mathrm{~N}$ and $2 \mathrm{~N}$
B. $1 \mathrm{~N}$ and $14 \mathrm{~N}$
C. $5 \mathrm{~N}$ and $6 \mathrm{~N}$
D. $6 \mathrm{~N}$ and $7 \mathrm{~N}$
Answer/Explanation
Solution:
If $\mathrm{A}$ and $\mathrm{B}$ are two vector then $R_{\text {resultant }}$ of these will vary from $(A-B)$ to $(A+B)$
$$
\begin{aligned}
& (F)_{\max }=A+B \\
& (F)_{\min }=A-B
\end{aligned}
$$
Option (A)- $1 N$ and $2 N » F_{\max }=3 N, F_{\min }=1 N$
Option (B)- $1 N$ and $14 N » F_{\max }=15 N, F_{\min }=13 N$
Option (C)- $5 N$ and $6 N » F_{\max }=11 N, F_{\min }=1 N$
Option (D)- $6 N$ and $7 N » F_{\max }=13 N, F_{\min }=1 N$
Q.3.2022-May-Physics_paper_1__TZ1_HL
Topic: Uncertainties and errors
Given: uncertainty in reading a laboratory thermometer is 0.5 °C
Calculate: When temperature of a liquid falls from 20 °C to 10 °C , percentage uncertainty in the change in temperature?
A. $2.5 \%$
B. $5 \%$
C. $7.5 \%$
D. $10 \%$
Answer/Explanation
Solution:
$
\begin{aligned}
& T_i=(10 \pm 0.5)^{\circ} \mathrm{C} \\
& T_f=(20 \pm 0.5)^{\circ} \mathrm{C}
\end{aligned}
$
$\begin{aligned} \Delta T & =T_f-T_i \\ & =(20-10) \pm(0.5+0.5) \\ & =10 \pm 1\end{aligned}$
\Delta T=(10 \pm 1)^{\circ}
percentage uncertainty
Q.4.2022-May-Physics_paper_1__TZ1_HL
Topic: Motion
Given: v is brought to rest, after travelling a distance d, by a frictional force$f$
Calculate: second identical block moving with initial speed u is brought to rest in the same distance d by a frictional force $\frac{f}{2}$ . What is u?
A. $ v$
B. $\frac{v}{\sqrt{2}}$
C. $\frac{v}{2}$
D. $\frac{v}{4}$
Answer/Explanation
Solution:
Let the mass of block be m ,then acceleration in first case when friction is f,
acceleration, $a=\frac{f}{m}$ from $[\mathrm{F}=\mathrm{ma}]$
$
\begin{aligned}
& v^2=u^2+2 a s \\
& v=\text { finel velocity } \\
& u=\text { initial velocity } \\
& a=\text { acceleration of body } \\
& s=\text { distance travvelled }
\end{aligned}\quad\text{(equation of motion )}
$
$V_f=0$
$V_i=V$
Using eq. of motion,
$0^2=V^2-2(\frac{f}{m})d$
$
\left(a d=\frac{V^2}{2}\right)
$
In case 2 , when friction is $\mathrm{f} / 2$ aceeleration will be $\frac{f}{2 m}$, which is half of previous acceleration,
$
\begin{aligned}
& u^2=\frac{2 a}{2 d}=a d \quad\left(a d=\frac{V^2}{2}\right) \\
& \therefore u=\frac{V}{\sqrt{2}}
\end{aligned}
$
Q.5.2022-May-Physics_paper_1__TZ1_HL
Topic: Motion
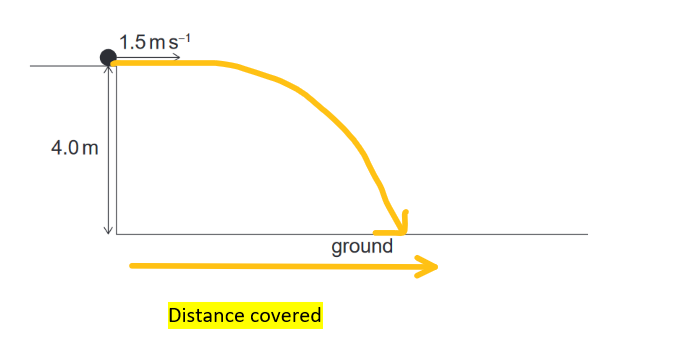
Given: A stone is kicked horizontally at a speed of $1.5 ~m s^{–1}$ , hits the ground 2.0 s later.
The height of the cliff is 4.0 m.

Calculate: What is the magnitude of the displacement of the stone?
A. $7.0 \mathrm{~m}$
B. $5.0 \mathrm{~m}$
C. $4.0 \mathrm{~m}$
D. $3.0 \mathrm{~m}$
Answer/Explanation
Solution:
Distance covered by stone along ground in $2 \mathrm{sec}=1.5 \times 2=3 \mathrm{~m}$, using [$distance =speed \times time$]