Question-1(a) :2022-nov-Chemistry_paper_2__TZ0_HL
Topic:
Given: Ammonium nitrate, $\mathrm{NH}_4 \mathrm{NO}_3$, is used as a high nitrogen fertilizer.
Calculate: the percentage by mass of nitrogen in ammonium nitrate. Use section 6 of the data booklet.
Answer/Explanation
Solution:
The molar mass of ammonium nitrate is:
$\mathrm{Molar \ mass \ of \ NH_4NO_3} = 14.01 \times 2 + 1.01 \times 4 + 16.00 \times 3 = 80.04 \ \mathrm{g/mol}$
The molar mass of nitrogen in ammonium nitrate is:
$\mathrm{Molar \ mass \ of \ N} = 14.01 \ \mathrm{g/mol}$
Therefore, the percentage by mass of nitrogen in ammonium nitrate is:
$\mathrm{% \ N} = \frac{\mathrm{Molar \ mass \ of \ N}}{\mathrm{Molar \ mass \ of \ NH_4NO_3}} \times 100%$
$\mathrm{% \ N} = \frac{2 \times 14.01 \mathrm{~g} \mathrm{~mol}^{-1}}{\left(2 \times 14.01 \mathrm{gmol}^{-1}+4 \times 1.01 \mathrm{gmol}^{-1}+3 \times 16.00 \mathrm{gmol}^{-1}\right)} \times 100 %$
$\mathrm{% \ N} = \frac{28.02 \mathrm{~g} \mathrm{~mol}^{-1}}{80.04 \mathrm{~g} \mathrm{~mol}^{-1}} \times 100 %$
$\mathrm{% \ N} = 0.3496 \times 100 % \approx 35.00 %$
Therefore, the percentage by mass of nitrogen in ammonium nitrate is approximately 35.00%.
Question-1 (b) :2022-nov-Chemistry_paper_2__TZ0_HL
Topic:
Discuss: with a reason, whether the ammonium ion is a Brønsted-Lowry acid or base.
Answer/Explanation
Solution:
For example, when ammonium ion reacts with water, it donates a proton to the water molecule to form hydronium ion and ammonia:
$\mathrm{NH_4^+ + H_2O \rightarrow H_3O^+ + NH_3}$
In this reaction, ammonium ion acts as an acid (donating a proton) and water molecule acts as a base (accepting a proton). Therefore, the ammonium ion is a Brønsted-Lowry acid.
Question-1[(c) (i)] :2022-nov-Chemistry_paper_2__TZ0_HL
Topic:
Given: $\mathrm{A} 0.20 \mathrm{~mol} \mathrm{dm}^{-3}$ solution of ammonium nitrate is prepared.
Calculate: the $\mathrm{pH}$ of an ammonium nitrate solution with $\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=1.07 \times 10^{-5} \mathrm{~mol} \mathrm{dm}^{-3}$. Use section 1 of the data booklet.
Answer/Explanation
Solution:
The concentration of $\mathrm{H_3O^+}$ is given as $1.07 \times 10^{-5}$ mol/dm$^3$.
Using the equilibrium constant expression and the concentrations of $\mathrm{H_3O^+}$ and $\mathrm{NH_4^+}$, we can solve for the concentration of $\mathrm{NH_3}$:
$K_\mathrm{a} = \dfrac{[\mathrm{H_3O^+}][\mathrm{NH_3}]}{[\mathrm{NH_4^+}]}$
$4.8 \times 10^{-10} = \dfrac{(1.07 \times 10^{-5})[\mathrm{NH_3}]}{(0.20)}$
$[\mathrm{NH_3}] = 2.56 \times 10^{-7}~\mathrm{mol/dm^3}$
The $\mathrm{pH}$ of the solution can be calculated using the concentration of hydronium ions, $\mathrm{H_3O^+}$, as follows:
$\mathrm{pH} = -\log([\mathrm{H_3O^+}])$
$\mathrm{pH} = -\log(1.07 \times 10^{-5})$
$\mathrm{pH} = 4.97$
Therefore, the $\mathrm{pH}$ of the ammonium nitrate solution is 4.97.
Question-1[(c) (ii)] :2022-nov-Chemistry_paper_2__TZ0_HL
Topic:
Discuss: Ammonium nitrate is neutralized with sodium hydroxide. Write the equation for the reaction.
Answer/Explanation
Solution:
$\mathrm{NH_4NO_3} + \mathrm{NaOH} \rightarrow \mathrm{NH_3} + \mathrm{NaNO_3} + \mathrm{H_2O}$
In this reaction, ammonium nitrate reacts with sodium hydroxide to produce ammonia, sodium nitrate, and water.
Question-1[(c) (iii)] :2022-nov-Chemistry_paper_2__TZ0_HL
Topic:
Given: A $20.00 \mathrm{~cm}^3$ sample of the $0.20 \mathrm{~mol} \mathrm{dm}^{-3}$ solution of ammonium nitrate is titrated with a $0.20 \mathrm{~mol} \mathrm{dm}^{-3}$ solution of sodium hydroxide.
Calculate: the $\mathrm{pH}$ at the equivalence point, to two decimal places using section 1 and 21 of the data booklet.
Answer/Explanation
Solution:
We can use the fact that at the equivalence point, the moles of the added sodium hydroxide will be equal to the moles of ammonium nitrate in the sample.
The moles of ammonium nitrate in the sample can be calculated as:
$n(\mathrm{NH_4NO_3}) = 0.20~\mathrm{moldm}^{-3} \times 0.02000\mathrm{dm}^3 = 0.0040~\mathrm{mol}$
Since the balanced equation for the neutralization reaction is:
$\mathrm{NH_4NO_3} + \mathrm{NaOH} \rightarrow \mathrm{NH_3} + \mathrm{NaNO_3} + \mathrm{H_2O}$
It can be seen that the moles of ammonia produced will also be equal to the moles of added sodium hydroxide at the equivalence point.
Therefore, the concentration of ammonia at the equivalence point can be calculated as:
$[\mathrm{NH_3}] = \dfrac{0.0040~\mathrm{mol}}{0.04000~\mathrm{dm}^3} = 0.10~\mathrm{mol~dm}^{-3}$
The value of $K_{\mathrm{b}}$ for ammonia can be found in section 21 of the data booklet, which gives:
$K_{\mathrm{b}} = 1.8 \times 10^{-5}$
Using this value, we can calculate the concentration of hydroxide ions at the equivalence point as:
$[\mathrm{OH^{-}}] = \sqrt{K_{\mathrm{b}}[\mathrm{NH_3}]} = \sqrt{1.8 \times 10^{-5}(0.10)} = 0.0013~\mathrm{mol~dm}^{-3}$
The $\mathrm{pOH}$ at the equivalence point can be calculated as:
$\mathrm{pOH} = -\log([\mathrm{OH^{-}}]) = -\log(0.0013) = 2.89$
Therefore, the $\mathrm{pH}$ at the equivalence point can be calculated as:
$\mathrm{pH} = 14.00 – \mathrm{pOH} = 14.00 – 2.89 = 11.11$
So the $\mathrm{pH}$ at the equivalence point is 11.11.
Question-1[(c) (iv)] :2022-nov-Chemistry_paper_2__TZ0_HL
Topic:
Sketch: the $\mathrm{pH}$ curve that would result from the titration of a $0.20 \mathrm{~mol}~ \mathrm{dm}^{-3}$ solution of ammonium nitrate with sodium hydroxide.
Answer/Explanation
Solution:
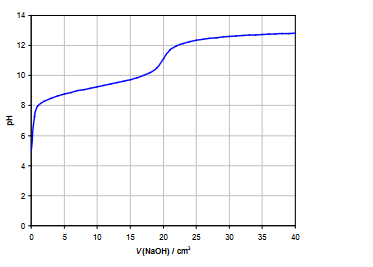
The graph shows the relationship between the volume of sodium hydroxide added to the ammonium nitrate solution and the resulting $\mathrm{pH}$ of the solution. Here’s a step-by-step explanation:
At the start of the titration, the ammonium nitrate solution has a low $\mathrm{pH}$ due to the presence of ammonium ions, which can hydrolyze in water to produce hydronium ions. The starting $\mathrm{pH}$ of the solution is typically between 2 and 7, depending on the exact concentration and conditions of the solution.
As sodium hydroxide is gradually added to the solution, it reacts with the ammonium ions to form ammonia and water. The ammonia can act as a weak base, which can accept protons from water to form hydroxide ions. As a result, the $\mathrm{pH}$ of the solution gradually increases.
The titration reaches its equivalence point when all of the ammonium ions in the solution have been neutralized by the sodium hydroxide. At this point, the $\mathrm{pH}$ of the solution reaches its maximum value, which is typically around 11 for the titration of ammonium nitrate with sodium hydroxide.
If more sodium hydroxide is added beyond the equivalence point, the excess hydroxide ions can react with water to form even more hydroxide ions, causing the $\mathrm{pH}$ of the solution to increase rapidly. The terminating $\mathrm{pH}$ of the solution is typically above 12.
Overall, the graph shows a non-symmetrical sigmoidal curve, which starts off with a shallow increase in $\mathrm{pH}$, followed by a steeper increase as the equivalence point is reached, and finally a sharp increase in $\mathrm{pH}$ as excess sodium hydroxide is added.
