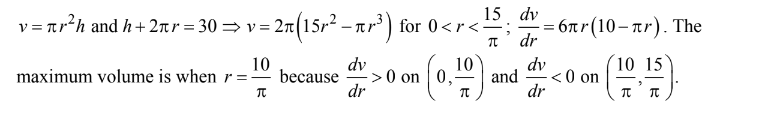AP Calculus AB: 5.10 Introduction to Optimization Problems – Exam Style questions with Answer- MCQ

AP PhysicsAP CalculusAP ChemistryAP Biology

AP Calculus AB-Questions and Answers - All Topics

Question

A puppy weighs 2.0 pounds at birth and 3.5 pounds two months later. If the weight of the puppy   during its first 6 months is increasing at a rate proportional to its weight, then how much will the puppy weigh when it is 3 months old?
(A) 4.2 pounds                (B) 4.6 pounds                        (C) 4.8 pounds                                (D) 5.6 pounds                                                        (E) 6.5 pounds

▶️Answer/Explanation

Ans:B

This is an example of exponential growth. We know from pre-calculus that \(w=\left ( \frac{3.5}{2} \right )^{\frac{t}{2}}\) an exponential function that meets the two given conditions. When t=3, w=4.630. Using calculus the student may translate the statement “increasing at a rate proportional to its weight” to mean exponential growth and write the equation w = 2ekt. Using the given

conditions, \(3.5 = 2e^{2k};\) In(1.75) = 2k;\( k = ·\frac{In(1.75)}{2}\) ;w=2et^{\frac{In(1.75)}{2}\)}\) . When t=3, w=4.630.

Question

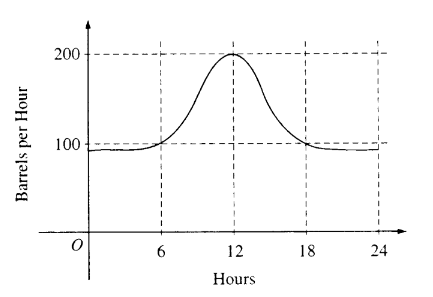
The flow of oil, in barrels per hour, through a pipeline on July 9 is given by the graph shown above. Of the following, which best approximates the total number of barrels of oil that passed through the pipeline that day?

(A) 500                          (B) 600                      (C) 2,400                         (D) 3,000                      (E) 4,800

▶️Answer/Explanation

Ans:D

Let r(t) be the rate of oil flow as given by the graph, where t is measured in hours. The total r(t)dt. This can be approximated by counting the squares number of barrels is given by \(\int_{0}^{24}r(t)dt\) below the curve and above the horizontal axis. There are approximately five squares with area 600 barrels. Thus the total is about 3,000 barrels.

Question

.A railroad track and a road cross at right angles. An observer stands on the road 70 meters south of the crossing and watches an eastbound train traveling at 60 meters per second. At how many
meters per second is the train moving away from the observer 4 seconds after it passes through the intersection?
(A) 57.60                      (B) 57.88                                                   (C) 59.20                                             (D) 60.00                                             (E) 67.40

▶️Answer/Explanation

Ans:A

Question

The position of an object attached to a spring is given by \(y(t)=\frac{1}{6}cos(5t)-\frac{1}{4}sin(5t) \), where t is time in seconds. In the first 4 seconds, how many times is the velocity of the object equal to 0?
(A) Zero

(B) Three

(C) Five

(D) Six

(E) Seven

▶️Answer/Explanation

Ans:D

Count the number of places where the graph of y  (t )  has a horizontal tangent line. Six places.

Question

Consider all right circular cylinders for which the sum of the height and circumference is 30 centimeters. What is the radius of the one with maximum volume?

(A) 3 cm                        (B) 10 cm                          (C) 20 cm                                     (D)      \(\frac{30}{\pi ^{2}}\)                        (E) \(\frac{10}{π}cm\)

▶️Answer/Explanation

Ans:E

More AP Calculus AB MCQ Questions..
Scroll to Top