Question
If \(x+3y^{\frac{1}{3}}=y\) ,what is \(\frac{\mathrm{d} y}{\mathrm{d} x}\) at the point (2,8) ?
A \(\frac{1}{3}\)
B \(\frac{3}{4}\)
C \(\frac{5}{4}\)
D \(\frac{4}{3}\)
▶️Answer/Explanation
Ans:D
The chain rule is the basis for implicit differentiation.\(1+y^{-\frac{2}{3}}\frac{\mathrm{d} y}{\mathrm{d} x}\)
The point
\(1+\frac{1}{4}\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\mathrm{d} y}{\mathrm{d} x}\Rightarrow \frac{3}{4}\frac{\mathrm{d} y}{\mathrm{d} x}=1\Rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{4}{3}\)
Question
Let f be the function defined by \(f(x)=-3+6x^{2}-2x^{3}\) What is the largest open interval on which the graph of f is both concave up and increasing?
A (0, 1)
B (1, 2)
C (0, 2)
D (2, ∞)
▶️Answer/Explanation
Ans:A
Question
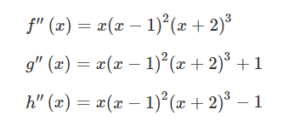
The twice-differentiable functions f, g, and h have second derivatives given above. Which of the functions f, g, and h have a graph with exactly two points of inflection?
A g only
B h only
C f and g only
D f, g, and h
▶️Answer/Explanation
Ans:C
Question
Let g be the function given by g(x)=’\(\int ^{x}_{3}(t^{2}-5t-14)dt\) . What is the x-coordinate of the point of inflection of the graph of g?
A -2
B\(\frac{5}{2}\)
C3
D7
▶️Answer/Explanation
Ans:B
To find the point of inflection of the graph of g,determine where g″ changes sign.
g′(x)\(=x^{2}-5x-14\)
g′′(x)=2x−5
Then g′′(x)=0 at \(x=\frac{5}{2}\). Since g′′(x)<0 for \(x<\frac{5}{2}\) and g′′(x)>0 for \(x>\frac{5}{2}\), the graph of g changes concavity at \(x=\frac{5}{2}\) and therefore, the graph of g has a point of inflection at \(x=\frac{5}{2}\).
