Curves of $f, f^{\prime}, f^{\prime \prime}$ and Curve Sketching
The following guidelines provide the information you need to sketch a curve $y=f(x)$. Not every item is relevant to every function.
Guidelines for Sketching a Curve
1. Domain
Identify the domain of $f$, that is, the set of values of $x$ for which $f(x)$ is defined.
2. Intercepts
To find the $x$-intercepts, let $y=0$ and solve for $x$. To find the $y$-intercepts, let $x=0$ and solve for $y$.
3. Symmetry
If $f(-x)=f(x)$, then $f$ is an even function and the curve is symmetric about the $y$-axis. If $f(-x)=-f(x)$, then $f$ is an odd function and the curve is symmetric about the origin. When replacing $y$ by $-y$ yields an equivalent equation, the curve is symmetric about the $x$-axis.
4. Asymptote
If either $\lim _{x \rightarrow \infty} f(x)=L$ or $\lim _{x \rightarrow-\infty} f(x)=L$, then the line $y=L$ is a horizontal asymptote of the curve $y=f(x)$.
If one of the following is true: $\lim _{x \rightarrow a^{+}} f(x)=\infty, \lim _{x \rightarrow a^{-}} f(x)=\infty, \lim _{x \rightarrow a^{+}} f(x)=-\infty$ or $\lim _{x \rightarrow a^{-}} f(x)=-\infty$, then the line $x=a$ is a vertical asymptote of the curve $y=f(x)$.
5. Intervals of Increasing or Decreasing
Compute $f^{\prime}(x)$. If $f^{\prime}(x)>0 \quad f$ is increasing and if $f^{\prime}(x)<0 \quad f$ is decreasing.
6. Relative Maximum and Relative Minimum Values
Find the critical numbers then use the first derivative test.
7. Points of Inflection and Concavity
Compute $f^{\prime \prime}(x)$. Inflection point occur where the direction of concavity changes. The curve is concave upward where $f^{\prime \prime}(x)>0$ and concave downward where $f^{\prime \prime}(x)<0$.
Example
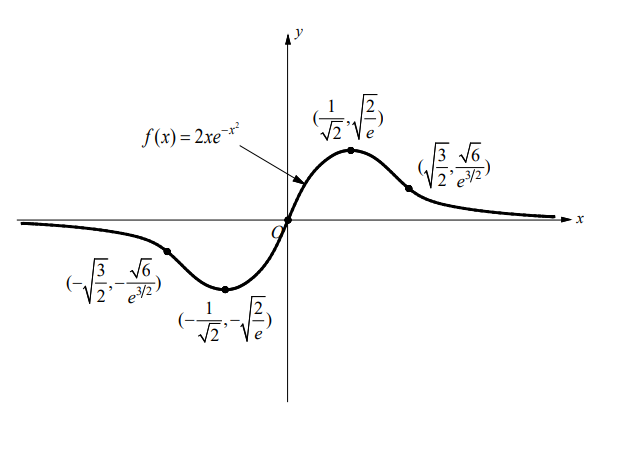
Sketch the graph of $f(x)=2 x e^{-x^2}$.
▶️Answer/Explanation
Solution
Domain of $f$ is $(-\infty, \infty)$.
2. $x$-intercepts: $(0,0) \quad y$-intercepts: $(0,0)$
3. $f(-x)=2(-x) e^{-(-x)^2}=-2 x e^{-x^2}=-f(x)$, so the curve is symmetric about the origin.
4. $\lim _{x \rightarrow-\infty} 2 x e^{-x^2}=\lim _{x \rightarrow-\infty} \frac{2 x}{e^{x^2}}=0, \lim _{x \rightarrow \infty} 2 x e^{-x^2}=\lim _{x \rightarrow \infty} \frac{2 x}{e^{x^2}}=0$, so $y=0$ is a horizontal asymptote.
$
\begin{aligned}
5. & f^{\prime}(x)=2\left(-2 x^2 e^{-x^2}+e^{-x^2}\right)=2 e^{-x^2}\left(1-2 x^2\right)=\frac{2\left(1-2 x^2\right)}{e^{x^2}} \\
& f^{\prime}(x)=0 \Rightarrow x= \pm \frac{1}{\sqrt{2}}
\end{aligned}
$
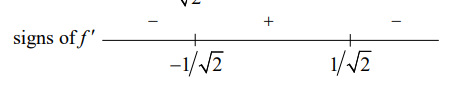
$f$ is increasing on $(-1 / \sqrt{2}, 1 / \sqrt{2})$.
$f$ is decreasing on $(-\infty,-1 / \sqrt{2})$ and $(1 / \sqrt{2}, \infty)$.
6. Relative maximum value $f(1 / \sqrt{2})=\sqrt{2 / e}$
Relative minimum value $f(-1 / \sqrt{2})=-\sqrt{2 / e}$
7. $f^{\prime \prime}(x)=4 x e^{-x^2}\left(2 x^2-3\right)$
$
f^{\prime \prime}(x)=0 \Rightarrow x=0, x= \pm \sqrt{3 / 2}
$
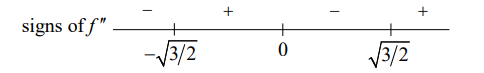
Points of inflection are $(0,0),\left(-\sqrt{3 / 2},-\sqrt{6} / e^{3 / 2}\right)$ and $\left(\sqrt{3 / 2}, \sqrt{6} / e^{3 / 2}\right)$.
$f$ is concave upward on $(-\sqrt{3 / 2}, 0)$ and $(\sqrt{3 / 2}, \infty)$.
$f$ is concave downward on $(-\infty,-\sqrt{3 / 2})$ and $(0, \sqrt{3 / 2})$.
Use the above information to sketch the graph of $f(x)=2 x e^{-x^2}$.
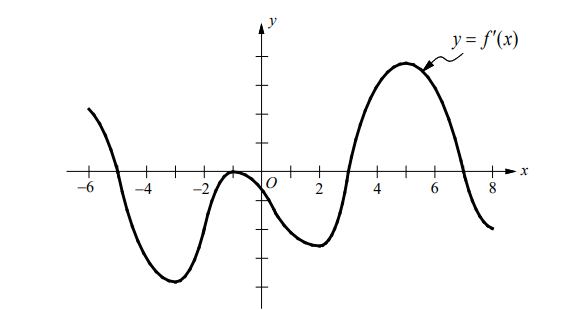
Note: This is the graph of $f^{\prime}$, not the graph of $f$.
Example 2
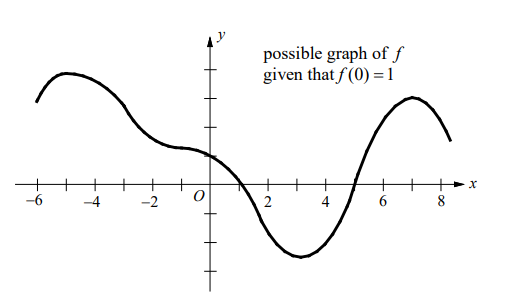
- The figure above shows the graph of $f^{\prime}$. The domain of $f$ is the set of all real numbers $x$ such that $-6 \leq x \leq 8$.
(a) For what values of $x$ does $f$ have a relative maximum?
(b) For what values of $x$ does $f$ have a relative minimum?
(c) For what values of $x$ does the graph of $f$ have a horizontal tangent?
(d) For what values of $x$ is the graph of $f$ concave upward?
(e) For what values of $x$ is the graph of $f$ concave downward?
(f) Suppose that $f(0)=1$. Sketch a possible graph of $f$.
▶️Answer/Explanation
Solution
(a) $f$ has relative maximum at $x=-5$ and 7 because $f^{\prime}$ changes from positive to negative at $x=-5$ and 7 .
(b) $f$ has relative minimum at $x=3$ because $f^{\prime}$ changes from negative to positive at $x=3$.
(c) The graph of $f$ has horizontal tangent at $x=-5,-1,3$, and 7 because $f^{\prime}(x)=0$ at these points.
(d) The graph of $f$ is concave upward on $(-3,-1)$ and $(2,5)$ because $f^{\prime}$ is increasing on these intervals.
(e) The graph of $f$ is concave downward on $(-6,-3),(-1,2)$ and $(5,8)$ because $f^{\prime}$ is decreasing on these intervals.
(f)
Exercises – Curves of $f, f^{\prime}, f^{\prime \prime}$ and Curve Sketching
Multiple Choice Questions
1. If $f$ is a function such that $f^{\prime}>0$ for $a<x<c, f^{\prime \prime}<0$ for $a<x<b$, and $f^{\prime \prime}>0$ for $b<x<c$ which of the following could be the graph of $f$ ?
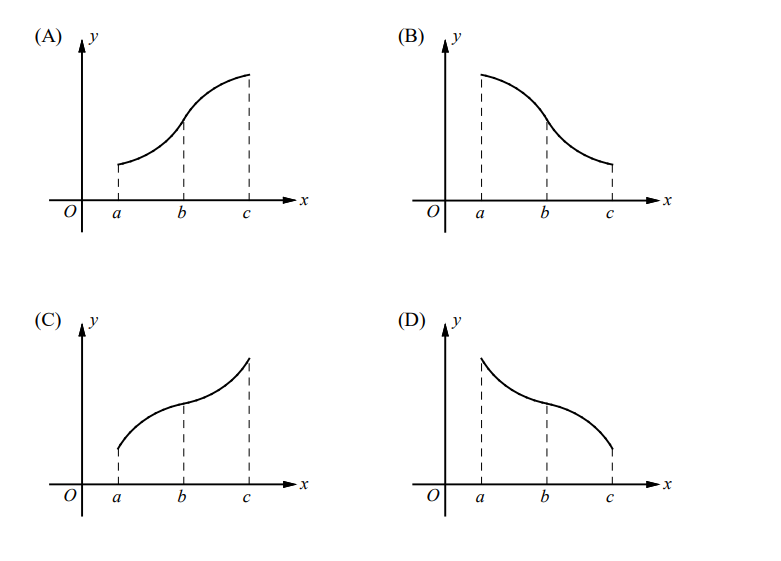
▶️Answer/Explanation
Ans:D
Question
- The graph of $f(x)=x e^{-x^2}$ is symmetric about which of the following
I. The $x$-axis
II. The $y$-axis
III. The origin
(A) I only
(B) II only
(C) III only
(D) II and III only
▶️Answer/Explanation
Ans:A
Question
- Let $f$ be the function given by $f(x)=\frac{-3 x^2}{\sqrt{3 x^4+1}}$. Which of the following is the equation of horizontal asymptote of the graph of $f$ ?
(A) $y=-3$
(B) $y=-\sqrt{3}$
(C) $y=\sqrt{3}$
(D) $y=3$
▶️Answer/Explanation
Ans:B
