The Total Change Theorem (Application of FTC)
The total change (accumulated change) in a quantity over a time period i the rate of change of the quantity.
$
\text { Total Change }=\int_a^b F^{\prime}(x) d x=F(b)-F(a)
$
This principle can be applied to all of the rates of change in natural and social sciences. The following are a few examples of these idea:
1. If $F^{\prime}(t)$ is the rate of growth of a population at time $t$, then
$
\int_a^b F^{\prime}(t) d t=F(b)-F(a)
$
is the increase in population between times $t=a$ and $t=b$.
2. If $F^{\prime}(t)$ is the rate of decomposition of a certain chemical, then
$
\int_a^b F^{\prime}(t) d t=F(b)-F(a)
$
is the total amount that has decomposed between times $t=a$ and $t=b$.
3. If $F^{\prime}(t)$ is the rate of consumption of a certain product, then
$
\int_a^b F^{\prime}(t) d t=F(b)-F(a)
$
is the total amount that has been consumed between times $t=a$ and $t=b$.
4. If $F^{\prime}(t)$ is the rate of change of temperature in a room, then
$
\int_a^b F^{\prime}(t) d t=F(b)-F(a)
$
is the total change in temperature between times $t=a$ and $t=b$.
Example 1
- For $0 \leq t \leq 60$, the rate of change of the number of mosquitoes at time $t$ days is modeled by $f(t)=6 \sqrt{t} \sin \left(\frac{t}{6}\right)$ mosquitoes per day. There are 1200 mosquitoes at time $t=0$.
(a) At time $t=20$, is the number of mosquitoes increasing or decreasing?
(b) According to the model, how many mosquitoes will be there at time $t=60$.
(c) To the nearest whole number, what is the maximum number of mosquitoes for $0 \leq t \leq 60 ?$
▶️Answer/Explanation
Solution
(a) Since $f(20)=6 \sqrt{20} \sin \left(\frac{20}{6}\right)=-5.113<0$, the number of mosquitoes is decreasing at $t=20$.
(b) The number of mosquitoes at time $t=60$ is
$
\begin{array}{ll}
1200+\int_a^b f(t) d t & \text { Initially there were } 1200 \text { mosquitoes. } \\
=1200+\int_0^{60} 6 \sqrt{t} \sin \left(\frac{t}{6}\right) d t & \int_0^{60} 6 \sqrt{t} \sin \left(\frac{t}{6}\right) d t \text { represents the increase in } \\
& \text { mosquitoe population between times } t=0 \text { and } t=60 . \\
=1200+282.272=1482.272 & \text { Use a graphing calculator to find the value of } \\
& \int_0^{60} 6 \sqrt{t} \sin \left(\frac{t}{6}\right) d t .
\end{array}
$
(c) $f(t)=0$ when $t=0, t=6 \pi, t=12 \pi, t=18 \pi$
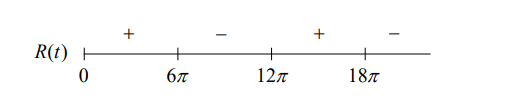
The absolute maximum number of mosquitoes occurs at $t=6 \pi$ or $t=18 \pi$.
$
\begin{gathered}
1200+\int_0^{6 \pi} 6 \sqrt{t} \sin \left(\frac{t}{6}\right) d t=1200+214.751=1414.751 \\
1200+\int_0^{18 \pi} 6 \sqrt{t} \sin \left(\frac{t}{6}\right) d t=1200+326.710=1526.710
\end{gathered}
$
There are 1415 mosquitoes at $t=6 \pi$ and 1527 mosquitoes at $t=18 \pi$, so the maximum number of mosquitoes is 1527 to the nearest whole number.
Example 2
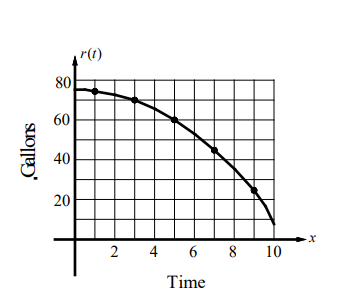
- Water leaks from a tank at a rate of $r(t)$ gallons per hour. The graph of $r$, for the time interval $0 \leq t \leq 10$ hours, is shown at the right. Use the midpoint Riemann sum with five intervals of equal length to estimate the total amount of water leaked out during the first 10 hours.
▶️Answer/Explanation
Solution
The five intervals are $[0,2],[2,4],[4,6],[6,8]$, and $[8,10]$. $75,70,60,45$, and 25 are the heights at each midpoint.
Total amount of water leaked out during the first 10 hours is $75 \cdot 2+70 \cdot 2+60 \cdot 2+45 \cdot 2+25 \cdot 2$ $=550$ gallons .
Example 3
Oil is pumped out from a tank at the rate of $\frac{20 e^{(-0.1 t)}}{1+e^{-t}}$ gallons per minute, where $t$ is measured in minutes. To the nearest gallon, how many gallons of oil are pumped out from a tank during the time interval $0 \leq t \leq 6$ ?
(A) 62
(B) 78
(C) 85
(D) 93
▶️Answer/Explanation
Ans:B
Example 4
Pollutant is released into a lake at the rate of $\frac{50 e^{-t / 2}}{\sqrt{t+1}}$ gallons per hour. To the nearest gallon, how many gallons of pollutant are released during the time interval $0 \leq t \leq 12$ ?
(A) 53
(B) 58
(C) 66
(D) 75
▶️Answer/Explanation
Ans:C
Example5
Oil is pumped into an oil tank at the rate of $S(t)$ gallons per hour during the time interval $0 \leq t \leq 8$ hours. During the same time interval, oil is removed from the tank at the rate of $R(t)$ gallons per hour. If the oil tank contained 200 gallons of oil at time $t=0$, which of the following expressions shows the amount of oil in the tank at time $t=6$ hours?
(A) $200+S(6)-R(6)$
(B) $200+S^{\prime}(6)-R^{\prime}(6)$
(C) $200+\int_0^6(S(t)-R(t)) d t$
(D) $200+\int_0^6\left(S^{\prime}(t)-R^{\prime}(t)\right) d t$
▶️Answer/Explanation
Ans:C
