Trigonometric Substitutions
Trigonometric Substitution
1. For integrals involving $\sqrt{a^2-u^2}$, let $u=a \sin \theta$. Then
$
\sqrt{a^2-u^2}=\sqrt{a^2-a^2 \sin ^2 \theta}=\sqrt{a^2\left(1-\sin ^2 \theta\right)}=\sqrt{a^2 \cos ^2 \theta}=a \cos \theta
$
2. For integrals involving $\sqrt{a^2+u^2}$, let $u=a \tan \theta$. Then
$
\sqrt{a^2+u^2}=\sqrt{a^2+a^2 \tan ^2 \theta}=\sqrt{a^2\left(1+\tan ^2 \theta\right)}=\sqrt{a^2 \sec ^2 \theta}=a \sec \theta
$
3. For integrals involving $\sqrt{u^2-a^2}$, let $u=a \sec \theta$. Then
$
\sqrt{u^2-a^2}=\sqrt{a^2 \sec ^2 \theta-a^2+}=\sqrt{a^2\left(\sec ^2 \theta-1\right)}=\sqrt{a^2 \tan ^2 \theta}=a \tan \theta
$
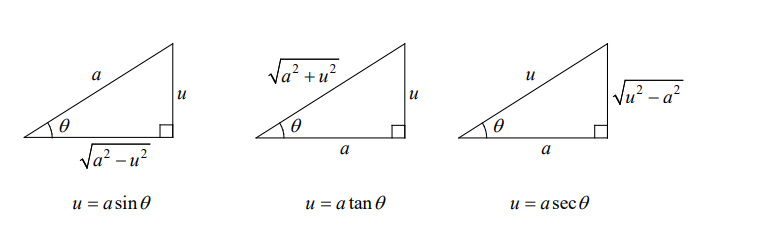
Note: $\operatorname{arcsec} x=\arccos \frac{1}{x}$
$
\operatorname{arccsc} x=\arcsin \frac{1}{x}
$
Example 1
- Evaluate $\int_0^2 \sqrt{4-x^2} d x$.
▶️Answer/Explanation
Solution
$\begin{aligned} & x=2 \sin \theta, d x=2 \cos \theta d \theta \\ & \sqrt{4-4 \sin ^2 \theta}=\sqrt{4\left(1-\sin ^2 \theta\right)}=2 \cos \theta \\ & \cos ^2 \theta=\frac{1+\cos 2 \theta}{2}\end{aligned}$
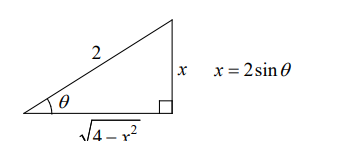
$\begin{aligned} & =2 \sin ^{-1}\left(\frac{x}{2}\right)+2\left(\frac{x}{2}\right)\left(\frac{\sqrt{4-x^2}}{2}\right)+C \\ & =2 \sin ^{-1}\left(\frac{x}{2}\right)+\frac{x \sqrt{4-x^2}}{2}+C\end{aligned}$
$\begin{aligned} & \int \sqrt{4-x^2} d x \\ & =\int \sqrt{4-4 \sin ^2 \theta} 2 \cos \theta d \theta \\ & =4 \int \cos ^2 \theta d \theta \\ & =4 \int \frac{1+\cos 2 \theta}{2} d \theta \\ & =2 \int(1+\cos 2 \theta) d \theta \\ & =2\left(\theta+\frac{1}{2} \sin 2 \theta\right)+C=2 \theta+\sin 2 \theta+C \\ & =2 \theta+2 \sin \theta \cos \theta+C \\ & =2 \sin ^{-1}\left(\frac{x}{2}\right)+2\left(\frac{x}{2}\right)\left(\frac{\sqrt{4-x^2}}{2}\right)+C \\ & =2 \sin ^{-1}\left(\frac{x}{2}\right)+\frac{x \sqrt{4-x^2}}{2}+C \\ & \end{aligned}$
Therefore
$
\int_0^2 \sqrt{4-x^2} d x=\left[2 \sin ^{-1}\left(\frac{x}{2}\right)+\frac{x \sqrt{4-x^2}}{2}\right]_0^2=2 \sin ^{-1}(1)=2 \cdot \frac{\pi}{2}=\pi
$
Example2
- Evaluate $\int \frac{d x}{\sqrt{9+x^2}}$.
▶️Answer/Explanation
Solution
$x=3 \tan \theta, d x=3 \sec ^2 \theta d \theta$
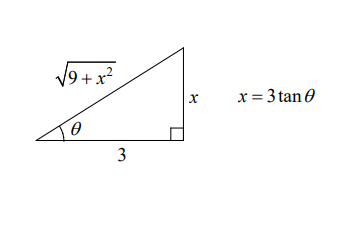
$\begin{aligned} & \int \frac{d x}{\sqrt{9+x^2}} \\ & =\int \frac{3 \sec ^2 \theta d \theta}{\sqrt{9+9 \tan ^2 \theta}} \\ & =\int \frac{3 \sec ^2 \theta d \theta}{3 \sec \theta} \\ & =\int \sec \theta d \theta \\ & =\ln |\sec \theta+\tan \theta|+C \\ & =\ln \left|\frac{\sqrt{9+x^2}}{3}+\frac{x}{3}\right|+C\end{aligned}$
Example 3
- $\begin{aligned} & x=2 \sec \theta, d x=2 \sec \theta \tan \theta d \theta \\ & \sqrt{4 \sec ^2 \theta-4}=\sqrt{4\left(\sec ^2 \theta-1\right)}=2 \tan \theta\end{aligned}$
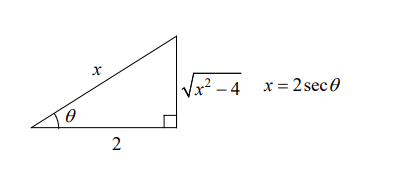
▶️Answer/Explanation
$\begin{aligned} & \int \frac{d x}{x^2 \sqrt{x^2-4}} \\ & =\int \frac{2 \sec \theta \tan \theta d \theta}{4 \sec ^2 x \sqrt{4 \sec ^2 \theta-4}} \\ & =\int \frac{2 \sec \theta \tan \theta d \theta}{4 \sec ^2 \theta 2 \tan \theta} \\ & =\frac{1}{4} \int \frac{d \theta}{\sec \theta} \\ & =\frac{1}{4} \int \cos \theta d \theta \\ & =\frac{1}{4} \sin \theta+C \\ & =\frac{1}{4} \frac{\sqrt{x^2-4}}{x}+C\end{aligned}$
Example4
- If the substitution $x=2 \tan \theta$ is made in $\int \frac{x^3}{\sqrt{x^2+4}} d x$, where $-\frac{\pi}{2}<\theta<\frac{\pi}{2}$, the resulting integral is
(A) $4 \int \tan ^2 \theta \sec \theta d \theta$
(B) $4 \int \tan ^2 \theta \sec ^2 \theta d \theta$
(C) $8 \int \tan ^3 \theta d \theta$
(D) $8 \int \tan ^3 \theta \sec \theta d \theta$
▶️Answer/Explanation
Ans:D
Example5
- $
\int_{\sqrt{2}}^2 \frac{1}{x \sqrt{x^2-1}} d x=
$
(A) $\frac{\pi}{18}$
(B) $\frac{\pi}{12}$
(C) $\frac{\pi}{6}$
(D) $\frac{\pi}{4}$
▶️Answer/Explanation
Ans:B
Example6
- $
\int \frac{1}{x^2 \sqrt{25-x^2}} d x=
$
(A) $-\frac{\sqrt{25-x^2}}{5 x^2}+C$
(B) $-\frac{\sqrt{25-x^2}}{25}+C$
(C) $-\frac{\sqrt{25-x^2}}{25 x}+C$
(D) $\frac{\sqrt{25-x^2}}{25 x^2}+C$
▶️Answer/Explanation
Ans:C
Example7
- If the substitution $x=\sec \theta$ is made in $\int \frac{\sqrt{x^2-1}}{x^4} d x$, where $-\frac{\pi}{2}<\theta<\frac{\pi}{2}$, the resulting integral is
(A) $\int \sec ^2 \theta \tan \theta d \theta+C$
(B) $\int \sec \theta \tan ^2 \theta d \theta+C$
(C) $\int \sin \theta \cos ^2 \theta d \theta+C$
(D) $\int \sin ^2 \theta \cos \theta d \theta+C$
▶️Answer/Explanation
Ans:D
