7.4 Logistic Equations $B C$
The differential equation
$
\frac{d P}{d t}=k P\left(1-\frac{P}{A}\right)
$
is called a logistic equation.
In this equation $P(t)$ is the size of the population at time $t, A$ is the carrying capacity (the maximum population that the environment is capable of sustaining in the long run), and $k$ is a constant.
If $0<P<A$, then $(1-P / A)$ is positive so, $d P / d t>0$ and the population increases.
If $P>A$, then $(1-P / A)$ is negative, so $d P / d t<0$ the population decreases.
In logistic equations
1. $\lim _{t \rightarrow \infty} \frac{d P}{d t}=0$
2. $\lim _{t \rightarrow \infty} P(t)=A$
3. The population is growing the fastest when $\boldsymbol{P}=\frac{\boldsymbol{A}}{2}$. (When $P$ is half the carrying capacity.)
4. The graph of $P(t)$ has a point of inflection at the point where $\boldsymbol{P}=\frac{\boldsymbol{A}}{2}$.
Figure 7-3 displays typical logistic curves.
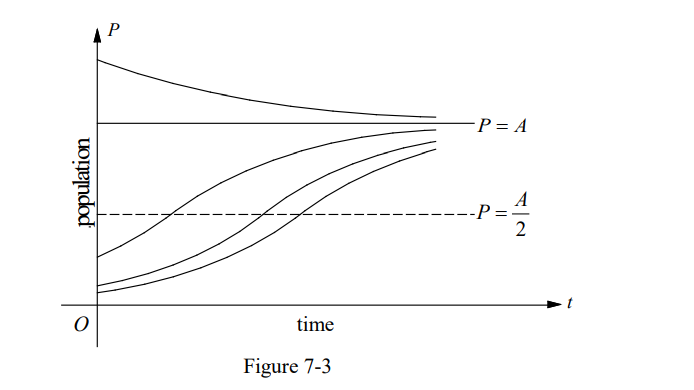
Solution curves for the logistic equations with different initial conditions
Example 1
A population is modeled by a function $P$ that satisfies the logistic differential equation $\frac{d P}{d t}=\frac{P}{2}\left(3-\frac{P}{20}\right)$, where the initial population $P(0)=100$ and $t$ is the time in years.
(a) What is $\lim _{t \rightarrow \infty} P(t)$ ?
(b) For what values of $P$ is the population growing the fastest?
(c) Find the slope of the graph of $P$ at the point of inflection.
▶️Answer/Explanation
Solution
(a) Write the differential equation in the standard form.
$
\begin{aligned}
& \frac{d P}{d t}=\frac{P}{2}\left(3-\frac{P}{20}\right)=\frac{3 P}{2}\left(1-\frac{P}{60}\right) \\
& \lim _{t \rightarrow \infty} P(t)=A=60
\end{aligned}
$
(b) The population is growing the fastest when $P=\frac{A}{2}$.
$
P=\frac{A}{2}=\frac{60}{2}=30
$
(c) The graph of $P$ has a point of inflection at $P=\frac{A}{2}$. So, when $P=30$,
$
\left.\frac{d P}{d t}\right|_{P=30}=\frac{30}{2}\left(3-\frac{30}{20}\right)=22.5
$
Example 2
- The population $P(t)$ of a species satisfies the logistic differential equation $\frac{d P}{d t}=3 P-0.0006 P^2$, where the initial population is $P(0)=1000$ and $t$ is the time in years. What is $\lim _{t \rightarrow \infty} P(t)$ ?
(A) 1000
(B) 2000
(C) 3000
(D) 5000
▶️Answer/Explanation
Ans:D
Example 3
- A healthy population $P(t)$ of animals satisfies the logistic differential equation $\frac{d P}{d t}=5 P\left(1-\frac{P}{240}\right)$, where the initial population is $P(0)=150$ and $t$ is the time in years. For what value of $P$ is the population growing the fastest?
(A) 48
(B) 60
(C) 120
(D) 240
▶️Answer/Explanation
Ans:C
Example 4
- A population is modeled by a function $P$ that satisfies the logistic differential equation $\frac{d P}{d t}=\frac{P}{5}\left(1-\frac{P}{150}\right)$, where the initial population is $P(0)=800$ and $t$ is the time in years. What is the slope of the graph of $P$ at the point of inflection?
(A) 5
(B) 7.5
(C) 10
(D) 12.5
▶️Answer/Explanation
Ans:B
Example 5
- A certain rumor spreads in a small town at the rate $\frac{d y}{d t}=y(1-3 y)$, where $y$ is the fraction of the population that has heard the rumor at any time $t$. What fraction of the population has heard the rumor when it is spreading the fastest?
(A) $\frac{1}{6}$
(B) $\frac{1}{5}$
(C) $\frac{1}{4}$
(D) $\frac{1}{3}$
▶️Answer/Explanation
Ans:A
