7.5 Euler’s Method $B C$
Euler’s Method is a numerical approach to approximate the particular solution of the differential equation $y^{\prime}=f(x, y)$ with an initial condition $y\left(x_0\right)=y_0$.
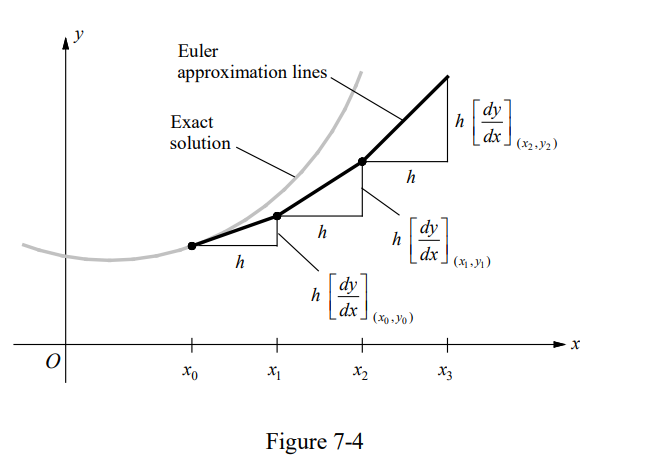
Using a small step $h$ and $\left(x_0, y_0\right)$ as a starting point, move along the tangent line until you arrive at the point $\left(x_1, y_1\right)$, where
$
\boldsymbol{x}_1=x_0+h \text { and } \boldsymbol{y}_1=y_0+\boldsymbol{h}\left[\frac{d y}{\boldsymbol{d x}}\right]_{\left(x_0, y_0\right)},
$
as shown in Figure 7-4.
Repeat the process with the same step size $h$ at a new starting point $\left(x_1, y_1\right)$. The values of $x_i$ and $y_i$ are as follows.
$\begin{array}{ll}x_1=x_0+h & y_1=y_0+h\left[\frac{d y}{d x}\right]_{\left(x_0, y_0\right)} \\ x_2=x_1+h & y_2=y_1+h\left[\frac{d y}{d x}\right]_{\left(x_1, y_1\right)} \\ \vdots & \vdots \\ x_{\boldsymbol{n}}=x_{n-1}+h & y_n=y_{n-1}+h\left[\frac{d y}{d x}\right]_{\left(x_{n-1}, y_{n-1}\right)}\end{array}$
Example 1
- Let $f$ be the function whose graph goes through the point $(1,-1)$ and whose derivative is given $y^{\prime}=2-\frac{y}{x}$. Use Euler’s method starting at $x=1$ with a step size of 0.5 to approximate $f(3)$.
▶️Answer/Explanation
Solution
Given $\frac{d y}{d x}=2-\frac{y}{x}, x_0=1, y_0=-1$, and $h=0.5$.
$\begin{aligned} f(1.5) \approx y_1 & =y_0+h\left[\frac{d y}{d x}\right]_{\left(x_0, y_0\right)} \\ & =-1+(0.5)\left(2-\frac{-1}{1}\right)=0.5 \quad x_0=1, y_0=-1\end{aligned}$
$\begin{aligned} f(2) \approx y_2 & =y_1+h\left[\frac{d y}{d x}\right]_{\left(x_1, y_1\right)} \\ & =0.5+(0.5)\left(2-\frac{0.5}{1.5}\right)=\frac{4}{3} \quad x_1=x_0+h=1+0.5=1.5, y_1=0.5\end{aligned}$
$\begin{aligned} f(2.5) \approx y_3 & =y_2+h\left[\frac{d y}{d x}\right]_{\left(x_2, y_2\right)} \\ & =\frac{4}{3}+(0.5)\left(2-\frac{4 / 3}{2}\right)=2 \quad x_2=x_1+h=1.5+0.5=2, y_2=4 / 3\end{aligned}$
$\begin{aligned} f(3) \approx y_4 & =y_3+h\left[\frac{d y}{d x}\right]_{\left(x_3, y_3\right)} \\ & =2+(0.5)\left(2-\frac{2}{2.5}\right)=2.6 \quad x_3=x_2+h=2+0.5=2.5, y_3=2\end{aligned}$
Example 2
- Let $y=f(x)$ be the solution to the differential equation $\frac{d y}{d x}=x-y+2$ with the initial condition $f(0)=2$. Use Euler’s method starting at $x=0$ with a step size of 0.5 to approximate $f(2)$.
▶️Answer/Explanation
Solution
Given $\frac{d y}{d x}=x-y+2, x_0=0, y_0=2$, and $h=0.5$.
$\begin{aligned} f(0.5) \approx y_1 & =y_0+h\left[\frac{d y}{d x}\right]_{\left(x_0, y_0\right)} \\ & =2+(0.5)(0-2+2)=2 \quad x_0=0, y_0=2\end{aligned}$
$\begin{aligned} f(1) \approx y_2 & =y_1+h\left[\frac{d y}{d x}\right]_{\left(x_1, y_1\right)} \\ & =2+(0.5)(0.5-2+2)=2.25 \quad x_1=0+0.5=0.5, y_1=2\end{aligned}$
$\begin{aligned} f(1.5) \approx y_3 & =y_2+h\left[\frac{d y}{d x}\right]_{\left(x_2, y_2\right)} \\ & =2.25+(0.5)(1-2.25+2)=2.625 \quad x_2=0.5+0.5=1, y_2=2.25\end{aligned}$
$\begin{aligned} f(2) \approx y_4 & =y_3+h\left[\frac{d y}{d x}\right]_{\left(x_3, y_3\right)} \\ & =2.625+(0.5)(1.5-2.625+2)=3.0625 \quad x_3=1+0.5=1.5, y_3=2.625\end{aligned}$
Example 3
- Let $y=f(x)$ be the solution to the differential equation $\frac{d y}{d x}=1+2 x-y$ with the initial condition $f(1)=2$. What is the approximation for $f(2)$ if Euler’s method is used, starting at $x=1$ with a step size of 0.5 ?
(A) 2.5
(B) 2.75
(C) 3.25
(D) 3.75
▶️Answer/Explanation
Ans:C
Example 4
- Let $y=f(x)$ be the solution to the differential equation $\frac{d y}{d x}=x-x y$ with the initial condition $f(0.5)=0$. What is the approximation for $f(2)$ if Euler’s method is used, starting at $x=0.5$ with a step size of 0.5 ?
(A) 0.825
(B) 0.906
(C) 1.064
(D) 1.178
▶️Answer/Explanation
Ans:B
Example 5
- Let $y=f(x)$ be the solution to the differential equation $\frac{d y}{d x}=\arctan (x y)$ with the initial condition $f(0)=1$. What is the approximation for $f(2)$ if Euler’s method is used, starting at $x=0$ with a step size of 1 ?
(A) $\frac{\pi}{2}$
(B) $1+\frac{\pi}{4}$
(C) $1+\frac{\pi}{2}$
(D) $\pi$
▶️Answer/Explanation
Ans:B
Example 6
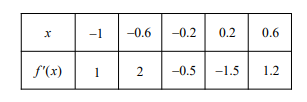
The table above gives selected values for the derivative of a function $f$ on the interval $-1 \leq x \leq 0.6$. If $f(-1)=1.5$ and Euler’s method is used to approximate $f(0.6)$ with step size of 0.8 , what is the resulting approximation?
(A) 1.9
(B) 2.1
(C) 2.3
(D) 2.5
▶️Answer/Explanation
Ans:A