8.4 Polar Coordinates and Slopes of Curves
Coordinate-System Conversion Formula
If a point $P$ has rectangular coordinates $(x, y)$ and polar coordinates $(r, \theta)$, then
$
\begin{array}{ll}
x=r \cos \theta, & y=r \sin \theta, \\
r^2=x^2+y^2, & \tan \theta=\frac{y}{x}(x \neq 0) .
\end{array}
$
The slope of the tangent line to the graph of $r=f(\theta)$ at point $(r, \theta)$ is
$
\frac{d y}{d x}=\frac{\frac{d y}{d \theta}}{\frac{d x}{d \theta}}=\frac{\frac{d}{d \theta}(r \sin \theta)}{\frac{d}{d \theta}(r \cos \theta)}=\frac{\frac{d r}{d \theta} \sin \theta+r \cos \theta}{\frac{d r}{d \theta} \cos \theta-r \sin \theta}, \text { where } \frac{d x}{d \theta} \neq 0 \text { at }(r, \theta) .
$
If $r>0$ and $\frac{d r}{d \theta}<0$ for $\alpha<\theta<\beta$, then $r$ is decreasing on this interval, which means the curve is getting closer to the origin.
If $r>0$ and $\frac{d r}{d \theta}>0$ for $\alpha<\theta<\beta$, then $r$ is increasing on this interval, which means the curve is getting farther from the origin.
If $\frac{d r}{d \theta}=0$, the curve is either closest to the origin or farthest from the origin.
Example 1
- A curve is defined by the polar equation $r=4 \sin (2 \theta)$ for $0 \leq \theta \leq \frac{\pi}{2}$.
(a) Graph the curve.
(b) Find the slope of the curve at the point where $\theta=\pi / 4$.
(c) Find an equation in terms of $x$ and $y$ for the line tangent to the curve at the point where $\theta=\frac{\pi}{4}$.
(d) Find an interval where the curve is getting closer to the origin.
(e) Find the value of $\theta$ in the interval $0 \leq \theta \leq \frac{\pi}{2}$ such that the point on the curve has the greatest distance from the origin.
▶️Answer/Explanation
Solution
(a)
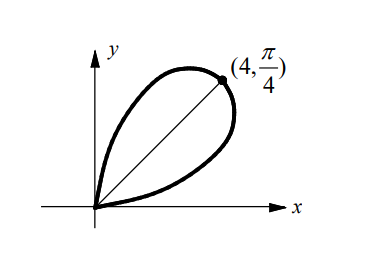
(b) $
\begin{aligned}
& x=r \cos \theta=4 \sin (2 \theta) \cos \theta, \frac{d x}{d \theta}=4(-\sin (2 \theta) \sin \theta+2 \cos (2 \theta) \cos \theta) \\
& \left.\frac{d x}{d \theta}\right|_{\theta=\frac{\pi}{4}}=4\left(-\sin \frac{\pi}{2} \sin \frac{\pi}{4}+2 \cos \frac{\pi}{2} \cos \frac{\pi}{4}\right)=-2 \sqrt{2} \\
& y=r \sin \theta=4 \sin (2 \theta) \sin \theta, \frac{d y}{d \theta}=4(\sin (2 \theta) \cos \theta+2 \cos (2 \theta) \sin \theta) \\
& \left.\frac{d y}{d \theta}\right|_{\theta=\frac{\pi}{4}}=4\left(\sin \frac{\pi}{2} \cos \frac{\pi}{4}+2 \cos \frac{\pi}{2} \sin \frac{\pi}{4}\right)=2 \sqrt{2}
\end{aligned}
$
The slope of a tangent line to the polar curve is $\frac{d y}{d x}$.
$
\left.\frac{d y}{d x}\right|_{\theta=\frac{\pi}{4}}=\left.\frac{d y / d \theta}{d x / d \theta}\right|_{\theta=\frac{\pi}{4}}=\frac{2 \sqrt{2}}{-2 \sqrt{2}}=-1
$
(c)
$
\begin{aligned}
& x=r \cos \theta=4 \sin (2 \theta) \cos \theta, x\left(\frac{\pi}{4}\right)=4 \sin \left(\frac{\pi}{2}\right) \cos \left(\frac{\pi}{4}\right)=\frac{4}{\sqrt{2}}=2 \sqrt{2} . \\
& y=r \sin \theta=4 \sin (2 \theta) \sin \theta, y\left(\frac{\pi}{4}\right)=4 \sin \left(\frac{\pi}{2}\right) \sin \frac{\pi}{4}=\frac{4}{\sqrt{2}}=2 \sqrt{2} . \\
& \left.\frac{d y}{d x}\right|_{\theta=\frac{\pi}{4}}=-1
\end{aligned}
$
The equation of tangent line is $y-2 \sqrt{2}=-1(x-2 \sqrt{2})$ or $y=-x+4 \sqrt{2}$.
(d)
The curve is getting closer to the origin when $\frac{d r}{d \theta}<0$.
$
\begin{aligned}
& \frac{d r}{d \theta}=8 \cos (2 \theta)<0 \Rightarrow \cos (2 \theta)<0 \Rightarrow \frac{\pi}{2}<2 \theta<\pi \\
& \Rightarrow \frac{\pi}{4}<\theta<\frac{\pi}{2}
\end{aligned}
$
(e) The point on the curve is farthest from the origin when $\frac{d r}{d \theta}=0$.
$
\frac{d r}{d \theta}=0 \Rightarrow \cos (2 \theta)=0 \Rightarrow 2 \theta=\frac{\pi}{2} \Rightarrow \theta=\frac{\pi}{4}
$
Example 2
- If $r=\theta-3 \sin \theta$ then $\frac{d r}{d \theta}$ at $(\pi, \pi)$ is
(A) 2
(B) $\pi$
(C) 4
(D) $2 \pi$
▶️Answer/Explanation
Ans:C
Example 3
- If $r=\frac{2}{1-\cos \theta}$ then $\frac{d r}{d \theta}$ at $\left(2, \frac{\pi}{2}\right)$ is
(A) -2
(B) -1
(C) 0
(D) 1
▶️Answer/Explanation
Ans:A
Example 4
- If $r=3 \sin \theta$ then $\frac{d y}{d x}$ at the point where $\theta=\frac{\pi}{3}$ is
(A) -2
(B) $-\sqrt{3}$
(C) -1
(D) $\frac{\sqrt{3}}{3}$
▶️Answer/Explanation
Ans:B
Example 5
- The equation of the polar curve is given by $r=\frac{8}{1-\cos \theta}$. What is the angle $\theta$ that corresponds to the point on the curve with $x$-coordinate -3 ?
(A) 1.248
(B) 1.356
(C) 1.596
(D) 2.214
▶️Answer/Explanation
Ans:D
