Question
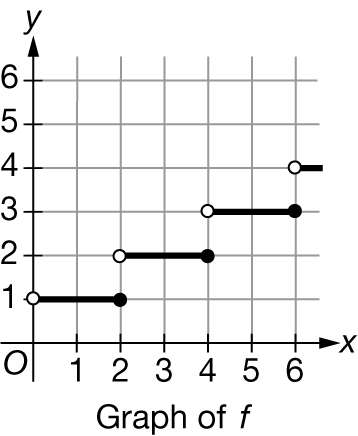
The graph of the function
is shown above. The value of 
is
A 2
B \(\frac{5}{2}\)
C 3
D nonexistent
Answer/Explanation
Ans:D
The limit exists if 
But here 
Question
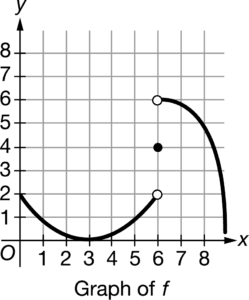
The graph of the function
is shown above. Which of the following expressions equals 2 ?
A f(6)
B 
C 
D 
Answer/Explanation
Ans:B
The value of the one-sided limit of
as
approaches 6 from the left, is determined by the part of the graph of f for
. As x
approaches 6 from the left, the values of
Question
The function
is given by\( f(x)=0.2x^{4}-10x^{3}-6.6x^{2}+15.4x-1.99\).For how many positive values of
does
?
A One
B Two9
C Three
D Four
Answer/Explanation
Ans:C
Since the polynomial
is a continuous function, 
is equal to
. The number of positive values of
for which the limit of
is equal to 6 can therefore be found by examining the graphs of
and
to see how many times they intersect. Care must be taken, however, since graphical representations of functions may miss important function behavior because of issues of scale. For example, a window of
and –
indicates that there is a value of b
near x=8 where the graph of y=f(x) crosses the line
. The scale along the
-axis is too large, however, to discern the behavior of
for values of x
near 0. Even using the interval 0
, the scale may suggest that the graph of y=f(x) is tangent to the line y=6 near
. Careful zooming, however, around
and
will show that the graph of
actually crosses the line
twice. Therefore, there are three positive values of b
for which
. The remaining solution to
is for a value of
Question
What is \(\lim_{x\rightarrow \frac{\pi }{4}}\tan x\) ?
(A) -1
(B) 0
(C) 1
(D)\(\frac{\sqrt{2}}{2}\)
Answer/Explanation
Ans:(C)