Question
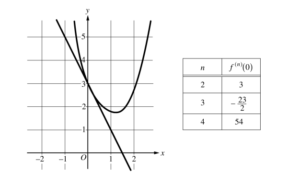
A function f has derivatives of all orders for all real numbers x. A portion of the graph of f is shown above, along with the line tangent to the graph of f at x = 0. Selected derivatives of f at x = 0 are given in the table above.
(a) Write the third-degree Taylor polynomial for f about x = 0.
(b) Write the first three nonzero terms of the Maclaurin series for ex . Write the second-degree Taylor polynomial for ex f(x) about x = 0.
(c) Let h be the function defined b \(h(x)=\int_{0}^{x}f(t)dt.\) Use the Taylor polynomial found in part (a) to find an approximation for h(1).
(d) It is known that the Maclaurin series for h converges to h (x) for all real numbers x. It is also known that the individual terms of the series for h(1 ) alternate in sign and decrease in absolute value to 0. Use the alternating series error bound to show that the approximation found in part (c) differs from h(1 ) by at most 0.45.
Answer/Explanation
Ans:
(a) f (0) = 3 and f ‘(0) = -2
The third-degree Taylor polynomial for f about x = 0 is
\(3-2x+\frac{3}{2!}x^{2}+\frac{-\frac{23}{2}}{3!}x^{3}=3-2x+\frac{3}{2}x^{2}-\frac{23}{12}x^{3}.\)
(b) The first three nonzero terms of the Maclaurin series for ex are \(1+x+\frac{1}{2!}x^{2}.\)
The second-degree Taylor polynomial for ex f(x) about x = 0 is \(3\left ( 1+x+\frac{1}{2!}x^{2} \right )-2x(1+x)+\frac{3}{2!}x^{2}(1)\)
\(=3+(3-2)x+\left ( \frac{3}{2}-2+\frac{3}{2} \right )x^{2}\)
= 3 + x + x2.
(c) \(h(1)=\int_{0}^{1}f(t)dt\)
\(\approx \int_{0}^{1}\left ( 3-2t+\frac{3}{2}t^{2}-\frac{23}{12}t^{3} \right )dt\)
\(= \left [ 3t-t^{2}+\frac{1}{2}t^{3}-\frac{23}{48}t^{4} \right ]_{t=0}^{t=1}\)
\(=3-1+\frac{1}{2}-\frac{23}{48}=\frac{97}{48}\)
(d) The alternating series error bound is the absolute value of the first omitted term of the series for h(1).
\(\int_{0}^{1}\left ( \frac{54}{4!}t^{4} \right )dt=\left [ \frac{9}{20}t^{5} \right ]_{t=0}^{t=1}=\frac{9}{20}\)
\(Error \leq \left | \frac{9}{20} \right |=0.45\)
Question
The Taylor series for a function f about x = 1 is given by \(\sum_{n=1}^{\infty }(-1)^{n+1}\frac{2^{n}}{n}(x-1)^{n}\) and converges to f (x) for
|x – 1| < R, where R is the radius of convergence of the Taylor series.
(a) Find the value of R.
(b) Find the first three nonzero terms and the general term of the Taylor series for f ‘, the derivative of f, about x = 1.
(c) The Taylor series for f ‘ about x = 1, found in part (b), is a geometric series. Find the function f ‘ to which the series converges for |x – 1| < R. Use this function to determine f for |x – 1| < R.
Answer/Explanation
Ans:
(a) Let an be the nth term of the Taylor series.
\(\frac{a_{n+1}}{a_{n}}=\frac{(-1)^{n+2}2^{n+1}(x-1)^{n+1}}{n+1}\cdot \frac{n}{(-)^{n+1}2^{n}(x-1)^{n}}\)
\(=\frac{-2n(x-1)}{n+1}\)
\(\lim_{n\rightarrow \infty }\left | \frac{-2n(x-1)}{n+1} \right |=2|x-1|\)
\(2|x-1|<1\Rightarrow |x-1|<\frac{1}{2}\)
The radius of convergence is \(R = \frac{1}{2}.\)
(b) The first three nonzero terms are
2 – 4(x – 1) + 8(x- 1)2.
The general term is \((-1)^{n+1}2^{n}(x-1)^{n-1} for n\geq 1.\)
(c) The common ratio is − 2 (x-1).
\(f'(x)=\frac{2}{1-(-2(x-1))}=\frac{2}{2x-1}for |x-1|<\frac{1}{2}\)
\(f(x)=\int \frac{2}{2x-1}dx=In |2x-1| + C\)
f(1) = 0
In |1| + C = 0 ⇒ C = 0
\(f(x)=|2x-1| for |x-1|<\frac{1}{2}\)
Question
The Maclaurin series for In (1+x) is given by
\(x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}+…+(-1)^{n+1}\frac{x^{n}}{n}+…\)
On its interval of convergence, this series converges to In (1+x). Let f be the function defined by \(f(x)=x In \left ( 1+\frac{x}{3} \right ).\)
(a) Write the first four nonzero terms and the general term of the Maclaurin series for f.
(b) Determine the interval of convergence of the Maclaurin series for f. Show the work that leads to your answer.
(c) Let P4 (x) be the fourth-degree Taylor polynomial for f about . Use the alternating series error bound to find an upper bound for \(|p_{4}(2)-f(2)|.\)
Answer/Explanation
Ans:
(a) The first four nonzero terms are \(\frac{x^{2}}{3}-\frac{x^{3}}{2.3^{2}}+\frac{x^{4}}{3.3^{3}}-\frac{x^{5}}{4.3^{4}}.\)
The general terms is \((-1)^{n+1}\frac{x^{n+1}}{n\cdot 3^{n}}.\)
(b) 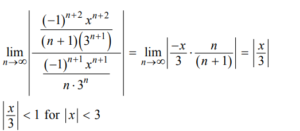
Therefore, the radius of convergence of the Maclaurin series for f is 3.
— OR —
The radius of convergence of the Maclaurin series for ln (1 + x) is 1, so the series for \(f(x)=xIn (1+\frac{x}{3})\) converges absolutely for \(\left | \frac{x}{3} \right |<1.\)
\(\left | \frac{x}{3} \right |<1\Rightarrow |x|<3\)
Therefore, the radius of convergence of the Maclaurin series for f is 3. When x = −3, the series is \(\sum_{n=1}^{\infty }(-1)^{n+1}\frac{(-3)^{n+1}}{n\cdot 3^{n}}=\sum_{n=1}^{\infty }\frac{3}{n},\) which diverges by comparison to the harmonic series. When x = 3, the series is \(\sum_{n=1}^{\infty }(-1)^{n+1}\frac{3^{n+1}}{n\cdot 3^{n}}=\sum_{n=1}^{\infty }(-1)^{n+1}\frac{3}{n},\) which converges by the alternating series test.
The interval of convergence of the Maclaurin series for f is −3< x ≤ 3 .
(c) By the alternating series error bound, an upper bound for|p4(2) – f(2)| is the magnitude of the next term of the alternating series.
\(\left | p_{4}(2)-f(2) \right |<\left | -\frac{2^{5}}{4.3^{4}} \right |=\frac{8}{81}\)
Question
f(0) = 0
f'(0) = 1
f(n+1) (0) = -n • f(n) (0) for all n ≥ 1
A function f has derivatives of all orders for −1 < x < 1. The derivatives of f satisfy the conditions above. The Maclaurin series for f converges to f(x) for |x| < 1.
(a) Show that the first four nonzero terms of the Maclaurin series for f are \(x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4},\) and write the general term of the Maclaurin series for f.
(b) Determine whether the Maclaurin series described in part (a) converges absolutely, converges conditionally, or diverges at x = 1. Explain your reasoning.
(c) Write the first four nonzero terms and the general term of the Maclaurin series for \(g(x)=\int_{0}^{x}f(t)dt.\)
(d) Let \(p_{n}\left ( \frac{1}{2} \right )\) represent the nth-degree Taylor polynomial for g about x = 0 evaluated at \(x= \frac{1}{2},\) where g is the function defined in part (c). Use the alternating series error bound to show that \(\left | p_{4} \left ( \frac{1}{2} \right )-g\left ( \frac{1}{2} \right )\right |<\frac{1}{500}.\)
Answer/Explanation
Ans:
(a) f(0) = 0
f'(0) = 1
f'(0) = -1(1) = -1
f”‘(0) = -2(-1) = 2
f(4) (0) = -3(2) = -6
The first four nonzero terms are
\(0+1x+\frac{-1}{2!}x^{2}+\frac{2}{3!}x^{3}+\frac{-6}{4!}x^{4}=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\frac{x^{4}}{4}\)
The general terms is \(\frac{(-1)^{n+1}x^{n}}{n}.\)
(b) For x = 1, the Maclaurin series becomes \(\sum_{n=1}^{\infty }\frac{(-1)^{n+1}x^{n}}{n}.\)
The series does not converge absolutely because the harmonic series diverges.
The series alternates with terms that decrease in magnitude to 0, and therefore the series converges conditionally.
(c) \(\int_{0}^{x}f(t)dt=\int_{0}^{x}\left ( t-\frac{t^{2}}{2}+\frac{t^{3}}{3} -\frac{t^{4}}{4}+….+\frac{(-)^{n+1}t^{n}}{n}+….\right )dt\)
\(\left [ \frac{t^{2}}{2}-\frac{t^{3}}{3\cdot 2} +\frac{t^{4}}{4\cdot 3}-\frac{t^{5}}{5\cdot 4}+….+\frac{(-)^{n+1}t^{n+1}}{(n+1)n}+…. \right ]_{t=0}^{t=x}\)
\(\frac{x^{2}}{2}-\frac{x^{3}}{6} +\frac{x^{4}}{12}-\frac{x^{5}}{20}+….+\frac{(-)^{n+1}t^{n+1}}{(n+1)n}+…. \)
(d) The terms alternate in sign and decrease in magnitude to 0. By the alternating series error bound, the error \(\left | p_{4}\left ( \frac{1}{2} \right )-g\left ( \frac{1}{2} \right ) \right |\) is bounded by the magnitude of the first unused term, \(\left | -\frac{(1/2)^{5}}{20} \right |.\)
Thus, \(\left | p_{4}\left ( \frac{1}{2} \right )-g\left ( \frac{1}{2} \right ) \right |\leq \left | -\frac{(1/2)^{5}}{20} \right |=\frac{1}{32\cdot 20}<\frac{1}{500}.\)
Question
The Maclaurin series for a function f is given by \(\sum_{n=1}^{\infty }\frac{(-3)^{n-1}}{n}x^{n}=x-\frac{3}{2}x^{2}+3x^{3}-…+\frac{(-3)^{n-1}}{n}x^{n}+…\) and
converges to f(x) for |x| < R , where R is the radius of convergence of the Maclaurin series.
(a) Use the ratio test to find R.
(b) Write the first four nonzero terms of the Maclaurin series for f ‘, the derivative of f. Express f ‘ as a rational function for |x| < R .
(c) Write the first four nonzero terms of the Maclaurin series for ex. Use the Maclaurin series for ex to write the third-degree Taylor polynomial for g (x) = ex f (x) about x = 0.
Answer/Explanation
Ans:
(a) Let an be the nth term of the Maclaurin series.
\(\frac{a_{n+1}}{a_{n}}=\frac{(-3)^{n}x^{n+1}}{n+1}\cdot \frac{n}{(-3)^{n-1}x^{n}}=\frac{-3n}{n+1}\cdot x\)
\(\lim_{n\rightarrow \infty }\left | \frac{-3n}{n+1}\cdot x \right |=3|x|\)
\(3|x|<1\Rightarrow |x|<\frac{1}{3}\)
The radius of convergence is \(R=\frac{1}{3}.\)
(b) The first four nonzero terms of the Maclaurin series for f ′ are 1 – 3x + 9x2 – 27x3.
\(f'(x)=\frac{1}{1-(-3x)}=\frac{1}{1+3x}\)
(c) The first four nonzero terms of the Maclaurin series for ex are \(1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}.\)
The product of the Maclaurin series for ex and the Maclaurin series for f is
\(\left ( 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+… \right )\left ( x-\frac{3}{2}x^{2}+3x^{3}-… \right )\)
\(=x-\frac{1}{2}x^{2}+2x^{3}+….\)
The third-degree Taylor polynomial for g(x) =ex f (x) about x = 0 is \(T_{3}(x)=x-\frac{1}{2}x^{2}+2x^{3}.\)
Question
(A) Express the function \(\frac{\sin x}{x}\) as a power series.
(B) Evaluate the indefinite integral \(\int \frac{\sin x}{x}dx\) as an infinite series.
(C) Approximate the definite integral \(\int_{0}^{1} \frac{\sin x}{x}dx\) to within an accuracy of three decimal places.
Answer/Explanation


Question
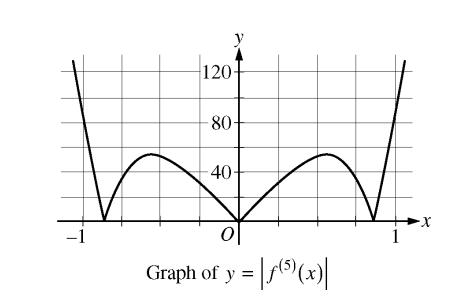
Let \(f(x)=sin(x^{2})+cos x.\) The graph of \(y = \left | f^{(5)}(x) \right |\) is shown above.
(a) Write the first four nonzero terms of the Taylor series for sin x about x = 0, and write the first four nonzero terms of the Taylor series for \(sin (x^{2})\) about x = 0.
(b) Write the first four nonzero terms of the Taylor series for cos x about x = 0. Use this series and the series for \(sin (x^{2})\), found in part (a), to write the first four nonzero terms of the Taylor series for f about x = 0.
(c) Find the value of f(6) (0).
(d) Let P4 (x) be the fourth-degree Taylor polynomial for f about x = 0. Using information from the graph of \(y = \left | f^{(5)}(x) \right |\) shown above, show that \(\left | p_{4}\left ( \frac{1}{4} \right )-f\left ( \frac{1}{4} \right ) \right |<\frac{1}{3000}.\)
Answer/Explanation
Ans:
(a)
\(sin x\approx x-\frac{x^{3}}{3!}+\frac{x^{5}}{5!}-\frac{x^{7}}{7!}\)
\(sin (x^{2})\approx x^{2}-\frac{x^{6}}{3!}+\frac{x^{10}}{5!}-\frac{x^{14}}{7!}\)
(b)
\(cos x\approx 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}\)
\(sin (x^{2})+cos (x)\approx1 -\frac{x^{2}}{2!}7x^{2}+\frac{x^{4}}{4!}-\frac{x^{6}}{6!}-\frac{x^{6}}{3!}\)
\(\approx1 -x^{2}\left ( \frac{1}{2}-1 \right )\frac{x^{4}}{4!}-x^{2}\left ( \frac{1}{6!}+\frac{1}{3!} \right )\)
(c)
By the definition of taylor series:
\(\frac{f^{t}(0)(x)^{6}}{6!}=x^{6}\left ( \frac{1}{6!}+\frac{1}{3!} \right )\)
\(\frac{f^{t}(0)}{6!}=-\left ( \frac{1+4.5.6}{6!} \right )\)
f(6) (0) = – (1+120)
= -121
(d)
\(\left | p_{4}\left ( \frac{1}{4} \right )-t\left ( \frac{1}{4} \right ) \right |\) is equivalent to the error of \(p_{4}\left ( \frac{1}{4} \right )\) Using the lagrangian error formulas we have
\(E<\frac{f^{(n+1)}(x)x^{n+1}}{(n+1)!}=\frac{f^{(5)}\left ( \frac{1}{4} \right )\cdot \left ( \frac{1}{4} \right )^{5}}{5!}\)
\(=\frac{f^{(5)}\left ( \frac{1}{4} \right )}{120\cdot 102t}\)
Looking at the graph, we see that \(f^{(5)}\left ( \frac{1}{4} \right )\) is a number less that 40.
If it were 40, then the maximum error would be \(\frac{40}{120.102t}=\frac{1}{3.102t},\) which is less than 1/3000. Since \(f^{(5)}\left ( \frac{1}{4} \right )\) is less than 40 then the maximum error must be less than 1/3000 QE.D.
Question
The function g has derivatives of all orders, and the Maclaurin series for g is \(\sum_{n=0}^{\infty }(-1)^{n}\frac{x^{2n+1}}{2n+3}=\frac{x}{3}-\frac{x^{3}}{5}+\frac{x^{3}}{7}- …….\)
(a) Using the ratio test, determine the interval of convergence of the Maclaurin series for g.
(b) The Maclaurin series for g evaluated at \(x = \frac{1}{2}\) is an alternating series whose terms decrease in absolute value to 0. The approximation for \(g\left ( \frac{1}{2} \right )\) using the first two nonzero terms of this series is \(\frac{17}{120}.\) Show that this approximation differs from \(g\left ( \frac{1}{2} \right )\) by less than \(\frac{1}{200}.\)
(c) Write the first three nonzero terms and the general term of the Maclaurin series for g'(x).
Answer/Explanation
Ans:
(a) \(\left | \frac{x^{2n+3}}{2n+5}\cdot \frac{2n+3}{x^{2n+1}} \right |=\left ( \frac{2n+3}{2n+5} \right )\cdot x^{2}\)
\(\lim_{n\rightarrow \infty }=\left ( \frac{2n+3}{2n+5} \right )\cdot x^{2}=x^{2}\)
x2 < 1 ⇒ -1 < x < 1
The series converges when -1 < x < 1.
When x = -1, the series is \(-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-…..\)
This series converges by the Alternating Series Test.
When x = 1, the series is \(\frac{1}{3}-\frac{1}{5}+\frac{1}{7}-\frac{1}{9}+…..\)
This series converges by the Alternating Series Test.
Therefore, the interval of convergence is -1 ≤ x ≤ 1.
(b) \(\left | g\left ( \frac{1}{2} \right )-\frac{17}{20} \right |<\frac{\left ( \frac{1}{2} \right )^{5}}{7}=\frac{1}{224}<\frac{1}{200}\)
(c) \(g'(x)=\frac{1}{3}-\frac{3}{5}x^{2}+\frac{5}{7}x^{4}+…+(-1)^{n}\left ( \frac{2n+1}{2n+3} \right )x^{2n}+…\)
