Question: (10 points, suggested time 20 minutes)
A large boat like the one shown above has a mass M b and can displace a maximum volume Vb . The boat is floating in a river with water of density Pwater and is being loaded with steel beams each of density Psteel and volume Vsteel . The boat owners want to be able to carry as many beams as possible.
(a) Derive an expression for the maximum number N of steel beams that can be loaded on the boat without exceeding the maximum displaced volume, in terms of the given quantities and physical constants, as appropriate.
(b) The captain realizes that oil is leaking from the boat, creating a thin film of oil on the water surface. In one area of the oil film the surface looks mostly green. Explain in detail how constructive interference contributes to the green appearance. Assume the index of refraction of the oil is greater than the index of refraction of the water.
(c) Later the boat is floating down the river with the water current, heading for a town. The river has a width of 60 m and a constant depth and flows at a speed of 5 km /hr. Partway to the town, the river narrows to a width of 30 m while its depth remains the same. Calculate the speed of the water in the narrow section.
▶️Answer/Explanation
Ans:
(a)
Fb = Fwater + Fsteel
Pwater Vb 9 = Mb9 + Psteel Vsteel N9
\(N = \frac{P_{water}V_{b}-M_{b}}{P_{steel}V_{steel}}\)
(b)
The oil floats on the water and because its index of retraction is great than air, light that refleets off of the oil is phase shifted by half a wave length. Some light travels into the ail and is refracted more downward due to higher area of refraction then air. This light reflects off of the bottom of the oil layer and is not phase shifted as the water has a higher index of refraction than the oil, the light then travels back up and reflects out of the oil at the some angle as the light was reflected off the top of the oil. The light reflected from both processes B constructive at the green wave length because the distance it look the light to travel considering its lessened wavelength through the oil phase shifted it half a green light wavelength to match the green light reflected off the oil.
(c)
d = depth (m)
V1 A1 = V2 A2
\(V_{2}=\frac{V_{1}A_{1}}{A_{2}} = \frac{(5)(d)(60)}{d(30)}= 10 km/hr\)
Question: (12 points, suggested time 25 minutes)
A group of students design an experiment to investigate the relationship between the density and pressure of a sample of gas at a constant temperature. The gas may or may not be ideal. They will create a graph of density as a function of pressure. They have the following materials and equipment.
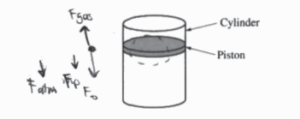
- A sample of the gas of known mass Mg in a sealed, clear, cylindrical container, as shown
- above, with a movable piston of known mass mp
- A collection of objects each of known mass mo
- A meterstick
(a)
i. Describe the measurements the students should take and a procedure they could use to collect the data needed to create the graph. Specifically indicate how the students could keep the temperature constant. Include enough detail that another student could follow the procedure and obtain similar data.
ii. Determine an expression for the absolute pressure of the gas in terms of measured quantities, given quantities, and physical constants, as appropriate. Define any symbols used that are not already defined.
iii. Determine an expression for the density of the gas in terms of measured quantities, given quantities, and physical constants, as appropriate. Define any symbols used that are not already defined.
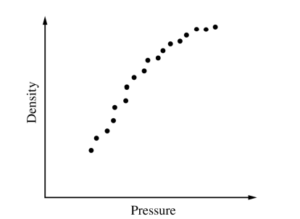
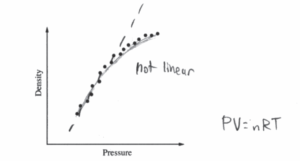
iv. The graph above represents the students’ data. Does the data indicate that the gas is ideal?
Describe the application of physics principles in an analysis of the graph that can be used to arrive at your answer.
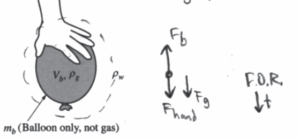
Another group of students propose that the relationship between density and pressure could also be obtained by filling a balloon with the gas and submerging it to increasing depths in a deep pool of water.
(b) Why could submerging the balloon to increasing depths be useful for determining the relationship between the density and pressure of the gas?
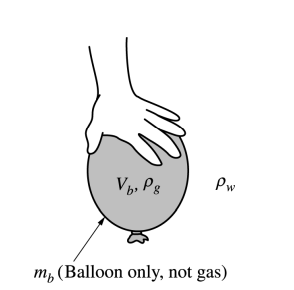
(c) The balloon is kept underwater in the deep pool by a student pushing down on the balloon, as shown above. Let Vb represent the volume of the inflated balloon, mb represent the mass of just the balloon (not including the mass of the gas), pg represent the density of the gas in the balloon, and pw represent the density of the water. Derive an expression for the force the student must exert to hold the balloon at rest under the water, in terms of the quantities given in this part and physical constants, as appropriate.
▶️Answer/Explanation
Ans:
(a)
i.
The temperature should remain constant if the container remains sealed and away from direct sunlight. Place objects on to the piston one at a time. Density will be Mg divided by the current volume of the gas (πr2h, r and h measured by meter stick). Pressure is equal to the added weight of the piston and objects divided by the area of the piston. Graph density as a function of pressure and repeat with different numbers of objects.
ii.
\(P_{0}=\frac{F_{atm}}{A}\)
Fatm = P.A
\(P = \frac{F}{A}= \frac{F_{p}+nF_{0}+P_{0}A}{\pi r^{2}}\)
\(\frac{g(m_{p}+m_{0})+P_{0}\pi r^{2}}{\pi r^{2}}=P\)
r = radius of piston
P0 = atm pressure
iii.
\(P = \frac{m}{V}\)
\(P = \frac{Mg}{\pi r^{2}h}\)
r = radius of piston
h = height of piston
iv.
The graph shows that density 2 is proportional to pressure. In an ideal gas, pressure in inversely proportional to volume, and volume is inversely proportional to density. Therefore, in an ideal gas, density should be directly proportional to pressure. Since this is not the case for this gas, this gas is not an ideal gas.
(b)
The pressure of the water increases with depth, which would decreases the volume (increasing the density since density is inversely proportional to volume) because of the pressure difference. This allows volume and density to be varied and graphed.
(c)
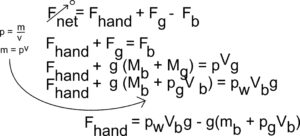
Question
A block of wood floats in water, with 2/3 of it submerged. The wood is then placed in oil, and 9/10 of it is submerged. Find the density of the wood, and of the oil.
▶️Answer/Explanation
Ans:
This problem involves floating objects, so weight of object = buoyant force mobj g = ρfluid Vdisp g
In general … mobj = ρobjVobj
Giving … ρobjVobj g = ρfluid Vdisp g … ρobjVobj = ρfluid Vdisp
Water Oil
ρobjVobj = ρfluid Vdisp ρobjVobj = ρfluid Vdisp
ρwV = (1000)(2/3 V) (666.67)V = ρoil (9/10 V)
ρw = 666.67 kg / m3 ρoil = 740.74 kg / m3
