Question
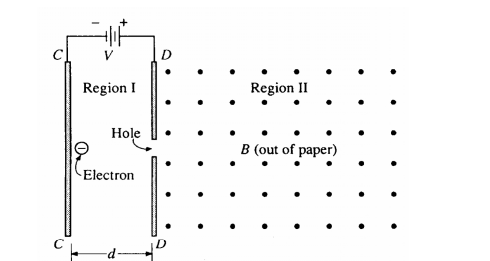
In region I shown above, there is a potential difference V between two large, parallel plates separated by a distance d. In region II, to the right of plate D, there is a uniform magnetic field B pointing perpendicularly out of the paper. An electron, charge –e and mass m, is released from rest at plate C as shown, and passes through a hole in plate D into region II. Neglect gravity.
a. In terms of e, V, m, and d, determine the following.
i. The speed vo of the electron as it emerges from the hole in plate D
ii. The acceleration of the electron in region I between the plates
b. On the diagram below do the following.
i. Draw and label an arrow to indicate the direction of the magnetic force on the electron as it enters the constant magnetic field. ii. Sketch the path that the electron follows in region II.
c. In terms of e, B, V, and m, determine the magnitude of the acceleration of the electron in region II.
▶️Answer/Explanation
Ans:
a) i) W = K … Vq = ½ mv2 … v = √ (2Ve/m)
ii) Fnet = ma Fe = ma Eq = ma (V/d) e = ma a = Ve / md
b) i & ii 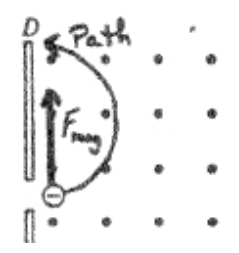
c) Fnet(c) = mac Fb = mac qvB = mac ac = evB/m
sub in v from part a-i → \(a_{c} = \frac{eB}{m}\sqrt{\frac{2Ve}{m}}\)
Question
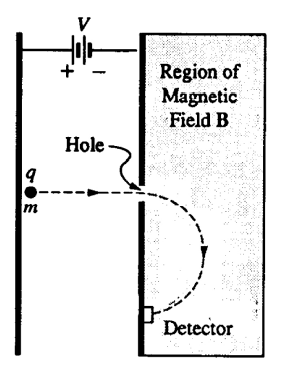
A particle of mass m and charge q is accelerated from rest in the plane of the page through a potential difference V between two parallel plates as shown. The particle is injected through a hole in the right-hand plate into a region of space containing a uniform magnetic field of magnitude B oriented perpendicular to the plane of the page. The particle curves in a semicircular path and strikes a detector.
a. i. State whether the sign of the charge on the particle is positive or negative.
ii. State whether the direction of the magnetic field is into the page or out of the page.
b. Determine each of the following in terms of m, q, V, and B.
i. The speed of the charged particle as it enters the region of the magnetic field B
ii. The force exerted on the charged particle by the magnetic field B
iii. The distance from the point of injection to the detector
iv. The work done by the magnetic field on the charged particle during the semicircular trip
▶️Answer/Explanation
Ans:
a) i) since the particle is accelerated toward the negatively charged plate, it must be positively charged
ii) The force on the particle due to the magnetic field is towards the center of the circular arc. By RHR the magnetic field must point out of the page.
b) i) W = K … Vq = ½ mv2 … v = √ (2Vq/m)
ii) Fb = qvB = qB (√ (2Vq/m) )
iii) Fnet(C) = mv2/r … qvB = mv2/ r … r = mv / Bq … distance is 2xr = 2mv/qB
iv) Work traveled in a circle at constant speed is zero as described in previous units.
Question
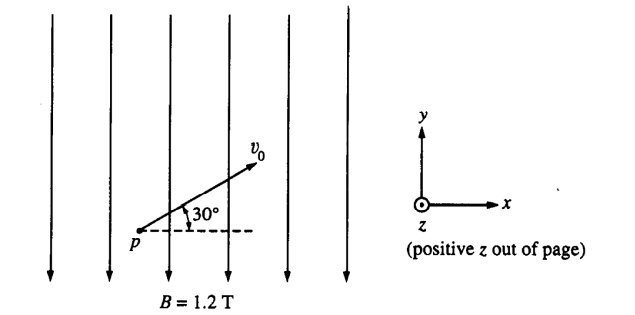
A uniform magnetic field of magnitude B = 1.2 teslas is directed toward the bottom of the page in the –y direction, as shown above. At time t = 0, a proton p in the field is moving in the plane of the page with a speed
vo = 4 x 107 meters per second in a direction 30° above the +x axis.
a. Calculate the magnetic force on the proton at t = 0.
b. With reference to the coordinate system shown above on the right, state the direction of the force on the proton at t = 0.
c. How much work will the magnetic field do on the proton during the interval from t = 0 to t = 0.5 second?
d. Describe (but do not calculate) the path of the proton in the field.
▶️Answer/Explanation
Ans:
a) Force is given by qvB ⊥, to make B ⊥ use B sin θ. Fb = qv B cos θ = (1.6×10–19)(4×107)(1.2)(cos30) = 6.7×10–12 N
b) Using the RHR for given direction, Force must be into the page in – z direction.
c) The magnetic force is perpendicular to the distance caused by the magnetic force at all points so work = 0
d) Since the velocity is not ⊥ to the field, this will not be a simple circle, though a version of circular motion will ensue. If the particle was traveling exactly horizontal, the motion would simply be a horizontal circle coming into and out of the page in the z direction. But since there is a component of the velocity that is in the upwards y direction, inertia will keep the particle moving upwards in the y direction in addition to circling in and out of the page. This will make it move in a helical fashion as shown here