Question
Select one of the following experiments:
I. The Michelson-Morley experiment
II. The Rutherford scattering experiment
III. The Compton scattering experiment
IV. The Davisson-Germer experiment
Clearly indicate the experiment you select and write an account of this experiment. Include in your account
a. a labeled diagram of the experimental setup
b. a discussion of the experimental observations
c. the important conclusions of the experiment
▶️Answer/Explanation
Ans:
I. Michelson–Morley
a) 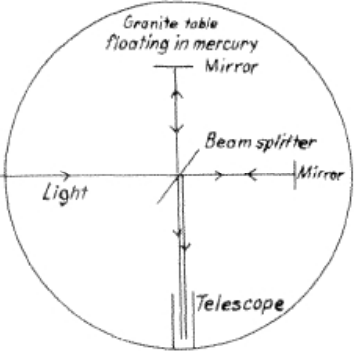
b) Interference fringes produced by the two reflected beams were observed in the telescope. It was found that these fringes did not shift when the table was rotated
b) The experiment refuted the hypothesis that there is a “luminiferous ether” in space through which light propagates. The null result of the experiment indicated that the speed of light is constant, independent of its direction of propagation.
II. Rutherford scattering
a)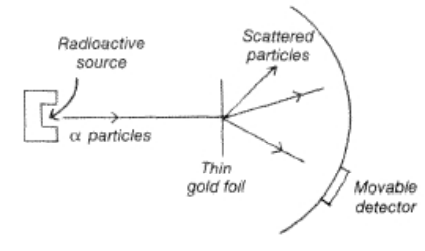
b) The detector revealed that alpha particles were scattered in various directions as they passed through the gold foil. While most of the particles were deflected only slightly, a few were scattered through very large angles.
c) Rutherford concluded that an atom is mostly empty space, with all the positive charge being concentrated in a small, dense nucleus. This experiment refuted the alternative “plum pudding” model of the atom, according to which positive charges were distributed throughout the atom.
III. Compton scattering
a)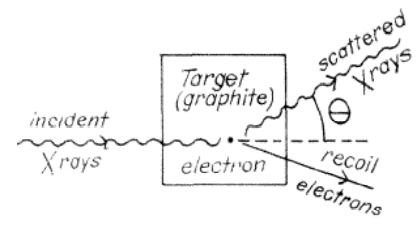
b) Compton observed that x–rays were scattered through various angles as a result of their collision with electrons in the target. The larger the angle through which an x–ray was scattered, the
more its wavelength had increased. The energy lost by the x–rays appeared as kinetic energy of the electrons.
c) The dependence of wavelength on scattering angle was explained by a model which treated x–rays as massless particles (photons) and used conservation of linear momentum and energy
to analyze photon–electron collisions. A model of x–rays as electromagnetic waves without particle properties could not explain the experimental data. Compton concluded that electromagnetic radiation has particle properties as well as wave properties.
IV. Davisson–Germer experiment
a)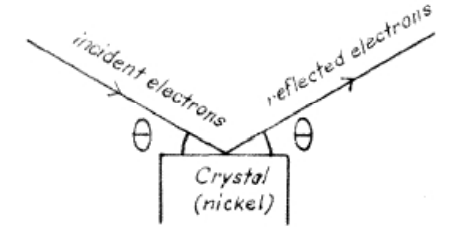
b) Electrons were reflected from the crystal, with the angle of reflection equal to the angle of incidence. The fraction of electrons reflected was unusually large for certain values of θ. The same phenomenon has earlier been observed in connection with scattering of x–rays and explained as an interference effect.
c) It was concluded that electrons have wave properties, with their wavelength inversely proportional to their linear momentum, and that the mathematics of waves can be used to explain the behavior of what had been though to be “particles”.
Question: (12 points, suggested time 25 minutes)
A student is given a glass block that has been specially treated so that the path of light can be seen as the light travels through the glass. The student is asked to design an experiment to measure the index of refraction of the glass. The light source available in the laboratory is a hydrogen lamp that emits red light of a known wavelength.
(a) A linear graph is to be used to determine the index of refraction of the glass. Indicate the quantities that should be graphed and describe how the graph could be used to determine the index of refraction of the glass.
(b) Outline an experimental procedure that could gather the necessary data. Include sufficient detail so that another student could follow your procedure. In addition to the glass block and the hydrogen lamp, the equipment in a typical classroom laboratory is available.
(c) Predict how the path of the light will change as it enters the glass. Support your prediction using a qualitative comparison of the speed of light in glass and the speed of light in air.
(d) Describe the process(es) by which red light from the lamp is produced by hydrogen atoms that are initially in the ground state. Draw and label an energy level diagram that supports the atomic process(es) you describe.
▶️Answer/Explanation
Ans:
n1Sinθ1 = n2Sinθ2 n1 drops out as it is equal to 1 in air.
Sinθ1 = n2Sinθ2 n2 should be solved for as it is the unknown.
\(n_{2} = \frac{Sin\theta _{1}}{Sin\theta _{2}}\) Thus Sinθ1 should be graphed on the y-axis and Sinθ2 should be graphed on the x-axis, so that n2 is equal to \(\frac{y}{x}\) on the slope of the graph.
(b)
The lamp should be set up using a slip so that only a thin beam of light is emitted. The glass block should be in line with this beam and placed on a turnable surface independent of the rest of the apparatus. Measurements can then be made by using a protractor to measure the angle the beam of light makes with the glass block just before entering, and the angle the beam of light makes with the glass block just after entering. All angles should be measured from the normal line. The first angle measured, or the N incident angle N, should be changed so that multiple measurements can be taken.
(c)
The path of the light will bend toward the normal line so that the angle of refraction is less than the angle of incidence. Looking at n1Sinθ1 = n2Sinθ2 we can see that when the index of refraction, n2, is greater than n1 then Sinθ2 must be less than Sinθ1 . Thus θ2< θ1 . The speed of light as it travels through glass is less than the speed of light as it travels through air. Therefore, since \(n = \frac{C}{V}\), when V is less n must increase. Thus nglass is greater than nair.
(d)
Hydrogen atoms in the ground state are excited by other photons. The atoms move to higher energy states as a result of being excited and gaining energy from the photons. The atoms then drop to lower energy states or the ground state and release some or all of the energy they absorbed, respectively.
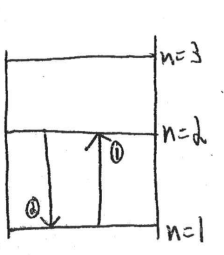
In step 1 energy is absorbed by the atom and it is excited to a higher energy level. In step 2 the energy is released in the form of a photon.
The atom could have also been excited of n=3 and then dropped to eithter n=2 or n=1. If it dropped to n=2 and then for n=1 the atom would release a photon for times – once for each energy level change
