Question
Some scientists want to perform electron diffraction experiments on crystals that have an intermolecular spacing of about \(10^{-10}\) m. They have two processes by which they can produce energetic electrons that can strike the crystals.
Process 1 is the beta decay of potassium into calcium: 
The mass of 
is 39.964000 u and the mass of 
is 39.962591 u. As an approximation, assume that the mass of the neutrino is negligible and that all the decay energy is acquired by the electron.
Process 2 is the emission of electrons when electromagnetic radiation of wavelength 7.5 nm shines on a copper surface with work function 4.7 eV.
(a) Describe a single criterion for determining whether each of these processes can be used to produce electrons for the diffraction experiments.
(b) Determine whether each of these processes could be used to produce electrons appropriate for the diffraction experiments. Justify your answers mathematically.
▶️Answer/Explanation
Ans:(a) For indicating an appropriate quantity to compare — either length or energy
For indicating the appropriate specic quantities to compare: de Broglie wavelengths of electrons and crystal spacing
OR
kinetic energy of electrons and kinetic energy needed to have a de Broglie wavelength equal to the crystal spacing
Example: The energy of electrons produced by each method is comparable to the energy of electrons with de Broglie wavelengths corresponding to the crystal spacing.
(b) For converting the electron energies to de Broglie wavelengths
OR
using the crystal spacing as a de Broglie wavelength to determine
the required electron energy Decay process
For determining the mass difference of the atoms
For converting the mass difference to energy
For correctly evaluating the energy against the crystal Photoelectric process
For determining the energy of the incident light
For determining the maximum kinetic energy K of the ejected electrons
For correctly evaluating the kinetic energy against the crystal
Example: Determine the electron kinetic energy needed for the electron to have a de Broglie
wavelength of\(10^{-10}\) m :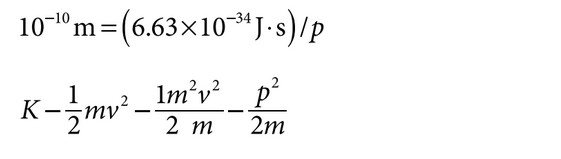
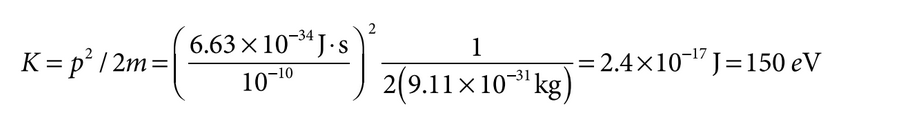
Determine the energy released by the decay reaction, which is converted to kinetic energy of the electron:
NOTE: is is four orders of magnitude larger than , so the wavelength will be two orders of magnitude smaller than desired. is process will not work well. Determine the maximum kinetic energy K of electrons emitted in the photoelectric effect: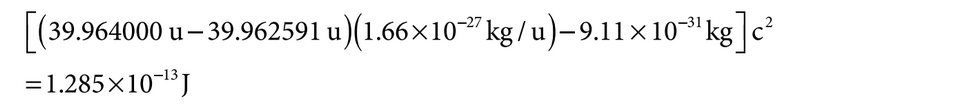 
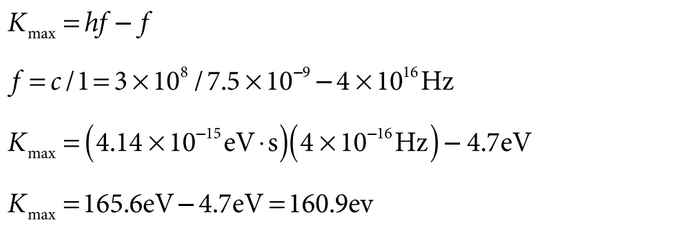
NOTE: is is comparable to 150 eV, so this process will work.
Question
Given the following information:
Proton mass = 1 .0078 u
Neutron mass = 1 .0087 u
Mass of \(^{226}_{88}Ra\) = 226.0244 u
(a) Determine the mass defect for this isotope of radium.
(b) What does this mass defect represent? Explain both qualitatively and quantitatively.
(c) If radium-88 naturally undergoes alpha decay, write down a nuclear reaction for this process. Be sure to show any energy required ( Q ) or released by this process. If a new element is formed and you are unsure of its symbol, you may use an X to represent that new element. Use the same isotope notation as that given in the information above.
(d) In the reaction in part (c), compare the total mass defects on the reactant side to the mass defect found in part (a):
_____ The reactants have the same mass defect.
_____ The reactants have a larger mass defect.
_____ The reactants have a smaller mass defect.
Justify your choice qualitatively, without using equations.
▶️Answer/Explanation
Ans:
(a) To find the mass defect, we first find the total constituent mass:
88 protons: m = (88)(1.0078) = 88.6864 u
138 neutrons: m = (138)(1.0087) = 139.2006 u
M(total) = 227.8870 u
Then we have:
Mass defect = 227.8870 u − 226.0244 u = 1.8626 u
(b) The mass defect represents the binding energy holding the nucleus together. This energy can be found by using Einstein’s equation \(E=mc^{2}\).
Using the conversion factor from the Table of Information for AP Physics 2:
1 u = 931 MeV/\(c^{2}\) and \(E=mc^{2}\)
The total binding energy (BE) is
BE = (931.5 MeV/u)(1.8626 u) = 1,735.0119 MeV
The binding energy per nucleon is
BE/nucleons = 1,735.0119/226 = 7.677 MeV
(c) \(^{226}_{88}Ra\rightarrow ^{222}_{86}Rn+^{4}_{2}He+Q\)
OR \(^{226}_{88}Ra\rightarrow ^{222}_{86}X+^{4}_{2}He+Q\)
(d) __X__ The reactants have a larger mass defect. Since this reaction is energy releasing, energy has left the nuclei. This energy has come from the mass, so the mass defect must be increased. The nucleons in the reactant side have greater binding energy on average than those on the product side.
Question
A student is investigating an unknown radioactive source with a Geiger counter. The Geiger counter clicks when it detects ionizing radiation but does not distinguish between alpha, beta, and gamma particles. The number of clicks indicates the number of ionizing events happening in the Geiger counter device due to the radiation it receives. The student puts a piece of paper between the radioactive source and the Geiger counter and does not notice a change in the clicking rate. However, the addition of one sheet of aluminum foil does decrease the rate. When several sheets of aluminum foil are layered in a thickness of about a centimeter, there are no clicks at all.
(a) What type of radiation is being emitted? Justify your choice by describing alpha, beta, and gamma particles and how they interact with matter.
(b) What is happening to the atomic number and mass number within each atom that emits this radiation? Is it possible to predict which radioactive atoms within the sample will be emitting the radiation next?
(c) Is the binding energy per nucleon within the radioactive atoms changing as the radiation is being emitted? If so, is the binding energy per nucleon going up or down? Justify your answer with a qualitative explanation.
(d) If the half-life of the radioactive material being investigated is 12 hours, what will happen to the click rate of the Geiger counter after 3 days?
▶️Answer/Explanation
Ans:
(a) Beta particles are being emitted. Alpha particles are stopped by paper, and gamma rays would penetrate the aluminum foil easily. Alpha particles are so easily stopped because they are big and highly charged. Beta particles have a single quantum of charge and are quite small, so they are harder to stop. Gamma rays are high frequency electromagnetic radiation and carry no charge. Thus they are the most difficult to stop.
(b) It is not possible to predict which specific radioactive atom will decay next. The process is random but defined by a certain probability. Upon emission of a beta particle, the atom will lose 4 units of mass and have its atomic number reduced by 2.
(c) The daughter nuclei will be more stable than before the beta particle was emitted. Therefore, its binding energy/nucleon will be higher. Another way to think about this is that the ejected electron is taking away energy in addition to its mass, leaving the daughter nuclei with a greater mass deficit per nucleon than before \((E=mc^{2})\).
(d) With a half-life of 12 hours, 3 days equals 6 half-lives. Therefore, the amount of radioactive atoms in the sample will have been reduced by approximately \((1/2)^{6}\) after 3 days. As a result, the click rate on the Geiger counter would also be reduced by this factor (1/64).