Focus Question: How is a field force different from a contact force?
We think of an electric charge as creating an electric field in the space around it. Any other charge in this space will have an electric force exerted on it.
Physics 2 Review – Electric Field Basics
- To test electric fields, we model the behavior of how a positive test charge (of magnitude +q) would respond to being placed in the field:
$\begin{gathered}E=\frac{\text { Force on test charge }}{\text { magnitude of test charge }} \\ \qquad \boldsymbol{E}=\frac{\boldsymbol{F}}{\boldsymbol{q}} \\ E=\frac{k Q q}{r^2} / \mathrm{q} \rightarrow \boldsymbol{E}=\frac{k \boldsymbol{Q}}{\boldsymbol{r}} \\ \text { *units of field }-\mathrm{N} / \mathrm{C}\end{gathered}$
- Electric field is vector quantity that measures the force per unit charge a charge would experience in the space around a charge:
$E=\frac{F}{q}=\frac{1}{4 \pi \epsilon_0} \frac{Q}{r^2}$
- If $\vec{r}$ is a unit vector drawn from $\mathrm{Q}$ to $\mathrm{q}$ :
$
\vec{E}=\frac{F}{q}=\frac{1}{4 \pi \epsilon_0} \frac{Q}{r^2} \hat{r}
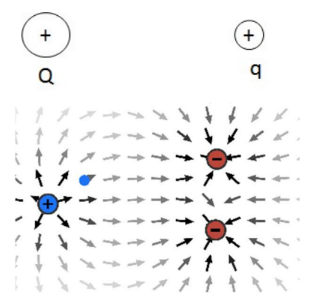
$ - By convention, the direction of electric field is in the direction a positive test charge would experience if placed in the field.
When Q is positive, then field at q points away from Q.
When Q is negative, the field at q points towards Q.
- By the principle of superposition, the total electric field is the vector sum of the fields due to all charges present.
Example A: The distance from $\mathrm{q}_1$ to $\mathrm{q}_2$ is $3.9 \mathrm{~m}$.
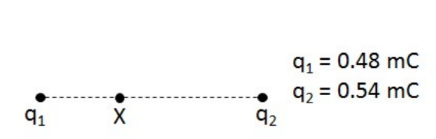
(a) If point $\mathrm{X}$ is $1.3 \mathrm{~m}$ from $\mathrm{q}_1$, then what is the magnitude of the electric field at point $X$ ?
(b) At what distance from q1 is the electric field intensity zero?
Answer/Explanation
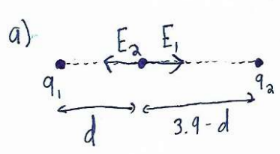
a) $\sum E=\frac{(9\times 10^{9\frac{Nm}{c^2}}(.48\times 10^{-3}C))}{(1.3m)^2}-\frac{(9\times 10^{9\frac{Nm}{c^2}}(.54\times 10^{-3}C))}{(2.6m)}$
$E=1.8 \times 10^6 \mathrm{C}$
b) $\begin{gathered}\sum E=\frac{\left(9 \times 10^9\right)\left(.48 \times 10^{-3}\right)}{d^2}-\frac{\left(9 \times 10^9\right)(.54 \times 10^{-3})}{(3.9-d)^2} \\ \Rightarrow d=1.89 \mathrm{~m}\end{gathered}$
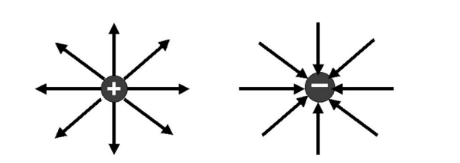
- Electric Field lines – drawn to indicate the direction of the force a test charge would experience. -Drawn outward from a positive charge and inwards towards a negative charge. -Stronger fields are drawn with more lines.
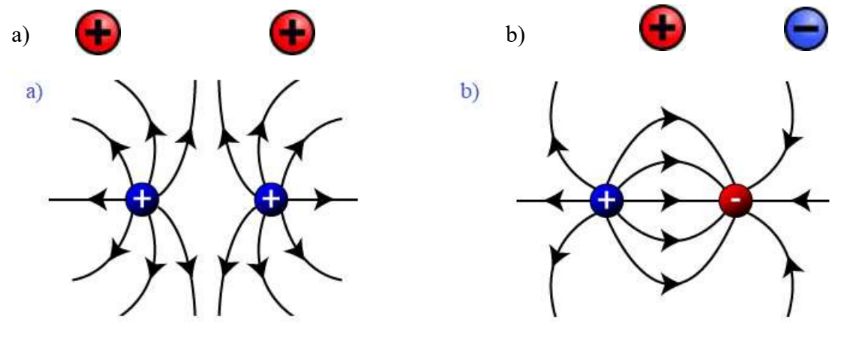
Example B: For each case of point charges below, draw the resulting electric field lines.
Answer/Explanation
Example C: Two charged, parallel plates are separated by a distance, d. The electric field intensity is 200 N/C. An electron with a speed of $4.0 × 10^{6}$m/s comes in from the left just above the negatively charged plate.
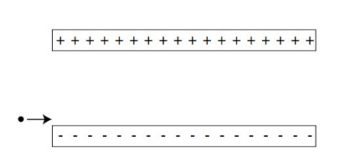
If the plates are 10 cm in length, how far has the electron moved in the y- direction during the time it takes to travel across the plates?
Answer/Explanation
The field goes from the top plate to the bottom plate. However, an electron goes against the field so it goes up in a parabolic path due its acceleration upwards. In the x-direction, it has a constant velocity.
$\frac{x-d_{i r e c t i o n}}{\Delta x=V_x t \Rightarrow} t=\frac{\Delta x}{V_x}=\frac{.10 \mathrm{~m}}{4 \times 10^6 \mathrm{~m} / \mathrm{s}}=2.5 \times 10^{-8} \mathrm{~s}$
$y$-direction
$
\begin{aligned}
& F=m a_y \Rightarrow E_q=m a_y \Rightarrow a_y=\frac{\left(200 \frac{\mathrm{N}}{\mathrm{n}}\right)\left(1.6 \times 10^{-19} \mathrm{C}\right)}{9.11 \times 10^{-31} \mathrm{~kg}}=3.5 \times 10^{13} \mathrm{~m} / \mathrm{s}^2 \\
& v_{y i}=0 \\
& \Delta y=v_y \cdot t^0+\frac{1}{2} a t^2=\frac{1}{2}\left(3.5 \times 10^{13} \mathrm{r} / \mathrm{s}^2\right)\left(2.5 \times 10^{-8} \mathrm{~s}\right)^2=.011 \mathrm{~m}
\end{aligned}
$
Electric Field of a Continuous Charge Distribution (Calculus)
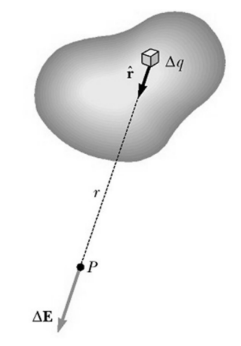
- For a continuous charge distribution, the total electric field is the vector sum of all infinitely small elements, ∆q, in the distribution (this is another way of stating the superposition principle):
$\begin{aligned} & d E=\frac{k}{r^2} d q \\ & \vec{E}=k \int \frac{d q}{r^2}\end{aligned}$
Where $d q=$ charge density $x$ (area, volume or length)
$\rho$ – volume charge density, $d q=\rho \mathrm{dV}$
$\sigma$ – surface charge density, $\mathrm{dq}=\sigma \mathrm{dA}$
$\lambda$-linear charge density, $\mathrm{dq}=\lambda \mathrm{dl}$
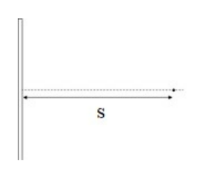
Example D: A Wire – Find the electric field at some distance, s, from a long straight insulating rod of charge +Q and length L at a point P.
Answer/Explanation
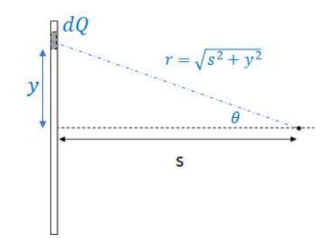
The electric field in y cancels due to symmetry. The rod is broken into a bunch of dQ’s of thickness dy where
$
d Q=\lambda d y=\frac{Q}{L} d y
$
$d E_x=\frac{k d Q}{r^2} \cos \theta=\frac{k \frac{Q}{L} d y}{s^2+y^2} \frac{s}{\sqrt{s^2+y^2}}=\frac{K Q s}{L} \frac{d y}{\left(s^2+y^2\right)^{\frac{3}{2}}}$
\begin{gathered}
\rightarrow E=\frac{k Q s}{L} \int_{-\frac{L}{2}}^{\frac{L}{2}} \frac{d y}{\left(s^2+y^2\right)^{\frac{3}{2}}} \rightarrow E=\frac{k Q s}{L}\left(\frac{y}{s^2 \sqrt{s^2+y^2}}\right)_{-\frac{L}{2}}^{\frac{L}{2}}=\frac{k Q}{s L}\left(\frac{\frac{L}{2}}{\sqrt{\left(\frac{L}{2}\right)^2+d^2}}-\frac{-\frac{L}{2}}{\sqrt{\left(-\frac{L}{2}\right)^2+d^2}}\right) \\
\rightarrow E=\frac{\boldsymbol{k Q}}{\boldsymbol{s \sqrt { \frac { L ^ { 2 } } { 4 } + s ^ { 2 } }}}
\end{gathered}
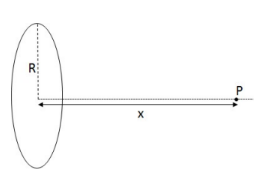
Example E: A Ring of Charge – A ring shaped conductor of radius R a carries total charge Q. Find the electric field at point P, a distance.
Answer/Explanation
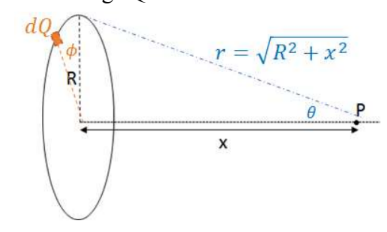
The ring is broken up into a bunch of dQ’s, which are small arc’s of length Rdφ. The variable φ is the angle a length from the center of the ring to the arc makes with the vertical. φ varies from 0 to 2π.
$
d Q=\text { charge density } * \text { arc length } \rightarrow d Q=\frac{Q}{2 \pi R} R d \phi
$
Again, only the $\mathrm{x}$-component is important since $\mathrm{y}$-cancels to symmetry.
\begin{aligned}
&d E_x=\frac{k d Q}{r^2} \cos \theta=\frac{k \lambda R d \phi}{R^2+x^2} \frac{x}{\sqrt{R^2+x^2}}=\frac{k x \frac{Q}{2 \pi R} R d \phi}{\left(R^2+x^2\right)^{\frac{3}{2}}}\\
&E=\int_0^{2 \pi} \frac{k x Q d \phi}{2 \pi\left(R^2+x^2\right)^{\frac{3}{2}}}=\frac{k x Q}{2 \pi\left(R^2+x^2\right)^{\frac{3}{2}}} \int_0^{2 \pi} d \phi \rightarrow \boldsymbol{E}=\frac{\boldsymbol{k x} \boldsymbol{Q}}{\left(\boldsymbol{R}^2+\boldsymbol{x}^2\right)^{\frac{3}{2}}}
\end{aligned}
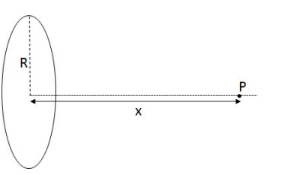
Example F: A Uniformly Charged Disk – Find the electric field due to a uniformly charge insulating disk of radius R at a point P perpendicular to the disc as shown.
Answer/Explanation
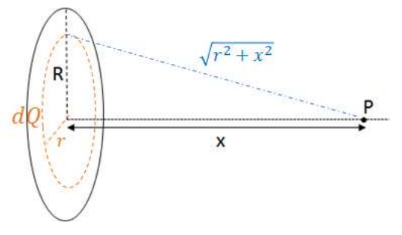
$\begin{gathered}d Q=\sigma d A=\sigma d\left(\pi r^2\right)=\sigma 2 \pi r d r \\ \sigma=\frac{Q}{\pi R^2}\end{gathered}$
$E=\int_0^R \frac{k(2 \pi r \sigma d r) x}{\left(r^2+x^2\right)^{\frac{3}{2}}}=\frac{\sigma x}{4 \varepsilon_0} \int_0^R \frac{2 r d r}{\left(r^2+x^2\right)^{\frac{3}{2}}}=\frac{\sigma}{2 \varepsilon_0}-\frac{\sigma x}{2 \varepsilon_0 \sqrt{R^2+x^2}}=\frac{\boldsymbol{Q}}{2 \varepsilon_0 \pi \boldsymbol{R}^2}-\frac{\boldsymbol{Q x}}{2 \boldsymbol{\varepsilon}_0 \pi \boldsymbol{R}^2 \sqrt{\boldsymbol{R}^2+\boldsymbol{x}^2}}$
Rate your understanding: Electric Fields

