Question
A wheel of 0.5 m radius rolls without slipping on a horizontal surface. The axle of the wheel advances at constant velocity, moving a distance of 20 m in 5 s. The angular speed of the wheel about its point of contact on the surface is
(A) \(2 radians.s^{-1}\)
(B) \(4radians.s^{-1}\)
(C) \(8 radians.s^{-1}\)
(D) \(16 radians.s^{-1}\)
(E) \(32 radians.s^{-1}\)
Answer/Explanation
Question
A disk of radius 0.1 m initially at rest undergoes an angular acceleration of 2.0 rad/ \(s^2\) . If the disk only rotates, find the total distance traveled by a point on the rim of the disk in 4.0 s.
(A) 0.4 m
(B) o.8 m
(C) 1.2 m
(D) 1.6 m
(E) 2.0 m
Answer/Explanation
Ans: D
Using the Big Five equation \(\Delta \theta = \frac{1}{2} (2 rad/s^2)(4.0s)^2 = 16 rad\)
Therefore, \(\Delta s = r\Delta \theta\) = ( 0.1 m)(16 rad) = 1.6 m. If you’re
worried about memorizing the Big Five equations, here’s
another method. The angular acceleration is 2.0 rad/\(s^2\) ,
which means it gets 2.0 rad/s faster every second. It starts
from rest. After 1 s, w = 2 rad/ s. After 2 s, w = 4 rad/ s. After 3 s, w = 6 rad/s. After 4.0 s, w = 8.o rad/s. That makes the
average angular velocity during these four seconds 4.0 rad/ s
(w increased linearly from o s to 8 s). Since the disk averages
4.0 rad/ s for 4 seconds, the angular distance traveled will be
16 rad, which brings you right back to \(\Delta s = r \Delta \theta\). One final alternative is to make a graph with w on the
vertical axis and t on the horizontal axis. The slope of an w
vs. t plot is a= 2.0 rad/\(s^2\) . The area under the graph from o
to 4 is the angular distance traveled by the point in the first
Question
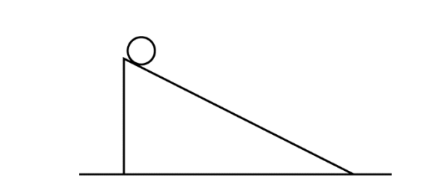
A sphere starts from rest at the top of a ramp, as shown above. It rolls without slipping down the ramp. The potential energy of the sphere-Earth system is zero at the bottom of the ramp. Which
of the following is true of the sphere when it reaches the bottom of the ramp?
(A) Its rotational kinetic energy equals the initial potential energy of the sphere-Earth system.
(B) Its translational kinetic energy equals the initial potential energy of the sphere-Earth system.
(C) Its translational kinetic energy and rotational kinetic energy are equal.
(D) The sum of its translational kinetic energy and rotational kinetic energy equals the initial potential energy of the sphere-Earth system.
(E) The sum of its translational kinetic energy and rotational kinetic energy equals the energy lost because of friction.
Answer/Explanation
Ans:D
Question
A ball with radius of 0.2 m rolls without slipping on a level surface. The center of mass of the ball moves at a constant velocity, moving a distance of 30 metres in 10 seconds. The angular speed of the ball about its point of contact on the surface is
(A) 0.6 rad/s
(B) 3 rad/s
(C) 8 rad/s
(D) 15 rad/s
(E) 60 rad/s
Answer/Explanation
Ans: D
The speed of the center of mass of the ball can be calculated using the equation, x = vt. Inserting the appropriate numbers gives
30m = v(10s)
v = 3 m/s
The angular speed of the ball about the contact point can be calculated using the equation, v = wr. The value for r is the distance from the contact point to the center of mass, which is the radius of the ball. Inserting the appropriate numbers gives
3 m/s = w (0.2 m)
Question
A particle is moving in a circle of radius 2 meters according to the relation θ = 3t2+ 2t, where θ is measured in radians and t in seconds. The speed of the particle at t = 4 seconds is
(A) 13 m/s (B) 16 m/s (C) 26 m/s (D) 52 m/s (E) 338 m/s
Answer/Explanation
Ans:D
