Question
Show that the set \(S\) of numbers of the form \({2^m} \times {3^n}\) , where \(m,n \in \mathbb{Z}\) , forms a group \(\left\{ {S, \times } \right\}\) under multiplication.
Show that \(\left\{ {S, \times } \right\}\) is isomorphic to the group of complex numbers \(m + n{\rm{i}}\) under addition, where \(m\), \(n \in \mathbb{Z}\) .
Answer/Explanation
Markscheme
Closure: Consider the numbers \({2^{{m_1}}} \times {3^{{m_1}}}\) and \({2^{{m_2}}} \times {3^{{n_2}}}\) where M1
\({m_1},{m_2},{n_1},{n_2}, \in \mathbb{Z}\) . Then,
Product \( = {2^{{m_1} + {m_2}}} \times {3^{{n_1} + {n_2}}}\) which \( \in S\) A1
Identity: \({2^0} \times {3^0} = 1 \in S\) A1
Since \(({2^m} \times {3^n}) \times ({2^{ – m}} \times {3^{ – n}}) = 1\) and \({2^{ – m}} \times {3^{ – n}} \in S\) R1
then \({2^{ – m}} \times {3^{ – n}}\) is the inverse. A1
Associativity: This follows from the associativity of multiplication. R1
[6 marks]
Consider the bijection
\(f({2^m} \times {3^n}) = m + n{\rm{i}}\) (M1)
Then
\(f({2^{{m_1}}} \times {3^{{n_1}}}) \times ({2^{{m_2}}} \times {3^{{n_2}}}) = f({2^{{m_1} + {m_2}}} \times {3^{{n_1} + {n_2}}})\) M1A1
\( = {m_1} + {m_2} + ({n_1} + {n_2}){\rm{i}}\) A1
\( = ({m_1} + {n_1}{\rm{i}}) + ({m_2} + {n_2}{\rm{i}})\) (A1)
\( = f({2^{{m_1}}} \times {3^{{n_1}}}) + f({2^{{m_2}}} \times {3^{{n_2}}})\) A1
[6 marks]
Question
The set \({{\rm{S}}_1} = \left\{ {2,4,6,8} \right\}\) and \({ \times _{10}}\) denotes multiplication modulo \(10\).
(i) Write down the Cayley table for \(\left\{ {{{\rm{S}}_1},{ \times _{10}}} \right\}\) .
(ii) Show that \(\left\{ {{{\rm{S}}_1},{ \times _{10}}} \right\}\) is a group.
(iii) Show that this group is cyclic.
Now consider the group \(\left\{ {{{\rm{S}}_1},{ \times _{20}}} \right\}\) where \({{\rm{S}}_2} = \left\{ {1,9,11,19} \right\}\) and \({{ \times _{20}}}\) denotes multiplication modulo \(20\). Giving a reason, state whether or not \(\left\{ {{{\rm{S}}_1},{ \times _{10}}} \right\}\) and \(\left\{ {{{\rm{S}}_1},{ \times _{20}}} \right\}\) are isomorphic.
Answer/Explanation
Markscheme
(i)
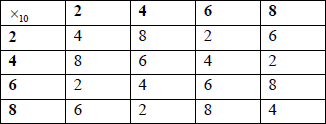 A2
A2
Note: Award A1 for one error.
(ii) closure: it is closed because no new elements are formed A1
identity: \(6\) is the identity element A1
inverses: \(4\) is self-inverse and (\(2\), \(8\)) form an inverse pair A1
associativity: multiplication is associative A1
the four group axioms are satisfied
(iii) any valid reason, e.g.
\(2\) (or \(8\)) has order \(4\), or \(2\) (or \(8\)) is a generator A2
[8 marks]
the groups are not isomorphic A1
any valid reason, e.g. \({{\rm{S}}_2}\) is not cyclic or all its elements are self-inverse R2
[3 marks]
Question
\(G\) is a group. The elements \(a,b \in G\) , satisfy \({a^3} = {b^2} = e\) and \(ba = {a^2}b\) , where \(e\) is the identity element of \(G\) .
Show that \({(ba)^2} = e\) .
Express \({(bab)^{ – 1}}\) in its simplest form.
Given that \(a \ne e\) ,
(i) show that \(b \ne e\) ;
(ii) show that \(G\) is not Abelian.
Answer/Explanation
Markscheme
EITHER
\(baba = ba{a^2}b\) M1
\( = b{a^3}b\) (A1)
\( = {b^2}\) A1
\( = e\) AG
OR
\(baba = {a^2}bba\) M1
\( = {a^2}{b^2}a\) (A1)
\( = {a^3}\) A1
\( = e\) AG
[3 marks]
\(bab = {a^2}bb\) (M1)
\( = {a^2}\) (A1)
\({(bab)^{ – 1}} = a\) A1
[3 marks]
(i) assume \(b = e\) M1
then \(a = {a^2}\) A1
\( \Rightarrow a = e\) which is a contradiction R1
(ii) if \(ab = ba\) M1
then \(ab = {a^2}b\) A1
\( \Rightarrow a = e\) which is a contradiction R1
[6 marks]
Question
Consider the set \(S = \{ 0,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5\} \) under the operation of addition modulo \(6\), denoted by \({ + _6}\).
Construct the Cayley table for \(\{ S,{\text{ }}{ + _6}\} \).
Show that \(\{ S,{\text{ }}{ + _6}\} \) forms an Abelian group.
State the order of each element.
Explain whether or not the group is cyclic.
Answer/Explanation
Markscheme
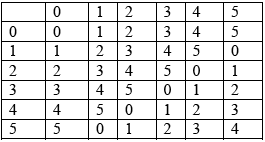 A2
A2
Note: A1 for one or two errors in the table, A0 otherwise.
closed no new elements A1
\(0\) is identity (since \(0 + a = a + 0 = a,{\text{ }}a \in S\)) A1
\(0\), \(3\) self inverse, \(1 \Leftrightarrow 5\) inverse pair, \(2 \Leftrightarrow 4\) inverse pair A1
all elements have an inverse
associativity is assumed over addition A1
since symmetry on leading diagonal in table or commutativity of addition A1
\( \Rightarrow \{ S,{\text{ }}{ + _6}\} \) is an Abelian group AG
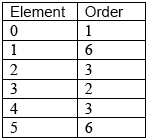 A2
A2
Note: A1 for one or two errors in the table, A0 otherwise.
since there is an element with order \(6\) OR \(1\) or \(5\) are generators R1
the group is cyclic A1
Question
The transformations T1, T2, T3, T4, in the plane are defined as follows:
T1 : A rotation of 360° about the origin
T2 : An anticlockwise rotation of 270° about the origin
T3 : A rotation of 180° about the origin
T4 : An anticlockwise rotation of 90° about the origin.
The transformation T5 is defined as a reflection in the \(x\)-axis.
The transformation T is defined as the composition of T3 followed by T5 followed by T4.
Copy and complete the following Cayley table for the transformations of T1, T2, T3, T4, under the operation of composition of transformations.
Show that T1, T2, T3, T4 under the operation of composition of transformations form a group. Associativity may be assumed.
Show that this group is cyclic.
Write down the 2 × 2 matrices representing T3, T4 and T5.
Find the 2 × 2 matrix representing T.
Give a geometric description of the transformation T.
Answer/Explanation
Markscheme
A2
[2 marks]
Note: Award A1 for 6, 7 or 8 correct.
the table is closed – no new elements A1
T1 is the identity A1
T3 (and T1) are self-inverse; T2 and T4 are an inverse pair. Hence every element has an inverse A1
hence it is a group AG
[3 marks]
all elements in the group can be generated by T2 (or T4) R1
hence the group is cyclic AG
[1 mark]
T3 is represented by \(\left( {\begin{array}{*{20}{c}}
{ – 1}&0 \\
0&{ – 1}
\end{array}} \right)\) A1
T4 is represented by \(\left( {\begin{array}{*{20}{c}}
0&{ – 1} \\
1&0
\end{array}} \right)\) A1
T5 is represented by \(\left( {\begin{array}{*{20}{c}}
1&0 \\
0&{ – 1}
\end{array}} \right)\) A1
[3 marks]
\(\left( {\begin{array}{*{20}{c}}
0&{ – 1} \\
1&0
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
1&0 \\
0&{ – 1}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{ – 1}&0 \\
0&{ – 1}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
0&{ – 1} \\
{ – 1}&0
\end{array}} \right)\) (M1)A1
Note: Award M1A0 for multiplying the matrices in the wrong order.
[2 marks]
a reflection in the line \(y = – x\) A1
[1 mark]
Question
The set \(S\) contains the eight matrices of the form\[\left( {\begin{array}{*{20}{c}}
a&0&0\\
0&b&0\\
0&0&c
\end{array}} \right)\]where \(a\), \(b\), \(c\) can each take one of the values \( + 1\) or \( – 1\) .
Show that any matrix of this form is its own inverse.
Show that \(S\) forms an Abelian group under matrix multiplication.
Giving a reason, state whether or not this group is cyclic.
Answer/Explanation
Markscheme
\(\left( {\begin{array}{*{20}{c}}
a&0&0\\
0&b&0\\
0&0&c
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
a&0&0\\
0&b&0\\
0&0&c
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{{a^2}}&0&0\\
0&{{b^2}}&0\\
0&0&{{c^2}}
\end{array}} \right)\) A1M1
\( = \left( {\begin{array}{*{20}{c}}
1&0&0\\
0&1&0\\
0&0&1
\end{array}} \right)\) A1
this shows that each matrix is self-inverse
[3 marks]
closure:
\(\left( {\begin{array}{*{20}{c}}
{{a_1}}&0&0\\
0&{{b_1}}&0\\
0&0&{{c_1}}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{{a_2}}&0&0\\
0&{{b_2}}&0\\
0&0&{{c_2}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{{a_1}{a_2}}&0&0\\
0&{{b_1}{b_2}}&0\\
0&0&{{c_1}{c_2}}
\end{array}} \right)\) M1A1
\( = \left( {\begin{array}{*{20}{c}}
{{a_3}}&0&0\\
0&{{b_3}}&0\\
0&0&{{c_3}}
\end{array}} \right)\)
where each of \({a_3}\), \({b_3}\), \({c_3}\) can only be \( \pm 1\) A1
this proves closure
identity: the identity matrix is the group identity A1
inverse: as shown above, every element is self-inverse A1
associativity: this follows because matrix multiplication is associative A1
\(S\) is therefore a group AG
Abelian:
\(\left( {\begin{array}{*{20}{c}}
{{a_2}}&0&0\\
0&{{b_2}}&0\\
0&0&{{c_2}}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{{a_1}}&0&0\\
0&{{b_1}}&0\\
0&0&{{c_1}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{{a_2}{a_1}}&0&0\\
0&{{b_2}{b_1}}&0\\
0&0&{{c_2}{c_1}}
\end{array}} \right)\) A1
\(\left( {\begin{array}{*{20}{c}}
{{a_1}}&0&0\\
0&{{b_1}}&0\\
0&0&{{c_1}}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{{a_2}}&0&0\\
0&{{b_2}}&0\\
0&0&{{c_2}}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{{a_1}{a_2}}&0&0\\
0&{{b_1}{b_2}}&0\\
0&0&{{c_1}{c_2}}
\end{array}} \right)\) A1
Note: Second line may have been shown whilst proving closure, however a reference to it must be made here.
we see that the same result is obtained either way which proves commutativity so that the group is Abelian R1
[9 marks]
since all elements (except the identity) are of order \(2\), the group is not cyclic (since \(S\) contains \(8\) elements) R1
[1 mark]

