Question
(i) Sum the series \(\sum\limits_{r = 0}^\infty {{x^r}} \) .
(ii) Hence, using sigma notation, deduce a series for
(a) \(\frac{1}{{1 + {x^2}}}\) ;
(b) \(\arctan x\) ;
(c) \(\frac{\pi }{6}\) .
Show that \(\sum\limits_{n = 1}^{100} {n! \equiv 3(\bmod 15)} \) .
Answer/Explanation
Markscheme
(i) \(\sum\limits_{r = 0}^\infty {{x^r}} = 1 + x + {x^2} + {x^3} + {x^4} + \ldots = \frac{1}{{1 – x}}\) A1
(ii) (a) replacing x by \( – {x^2}\) gives (M1)
\(\frac{1}{{1 – ( – {x^2})}} = 1 + ( – {x^2}) + {( – {x^2})^2} + {( – {x^2})^3} + {( – {x^2})^4} + \ldots \) A1
\(\frac{1}{{1 + {x^2}}} = 1 – {x^2} + {x^4} – {x^6} + {x^8} – \ldots \) (A1)
\( = \sum\limits_{r = 0}^\infty {{{( – 1)}^r}{x^{2r}}} \) A1 N2
(b) \(\arctan x = \int {\frac{{{\rm{d}}x}}{{1 + {x^2}}}} = x – \frac{{{x^3}}}{3} + \frac{{{x^5}}}{5} – \frac{{{x^7}}}{7} + \ldots + c\) M1A1
\(x = 0 \Rightarrow c = 0\) A1
\(\arctan x = \sum\limits_{r = 0}^\infty {{{( – 1)}^r}\frac{{{x^{2r + 1}}}}{{2r + 1}}} \) A1
(c) by taking \(x = \frac{1}{{\sqrt 3 }}\) M1
\(\arctan \frac{1}{{\sqrt 3 }} = \frac{\pi }{6} = \sum\limits_{r = 0}^\infty {\frac{{{{( – 1)}^r}{{\left( {\frac{1}{{\sqrt 3 }}} \right)}^{2r + 1}}}}{{2r + 1}}} \) A1
[11 marks]
\(\sum\limits_{n = 1}^{100} {n! = 1! + 2! + 3! + 4! + 5! + \ldots } \) M1
\( = 1 + 2 + 6 + 24 + 120 + \ldots \)
\( \equiv 1 + 2 + 6 + 24 + 0 + 0 + 0 + \ldots (\bmod 15)\) M1A1
\( \equiv 33(\bmod 15)\) A1
\( \equiv 3(\bmod 15)\) AG
[4 marks]
Question
Given that \({n^2} + 2n + 3 \equiv N(\bmod 8)\) , where \(n \in {\mathbb{Z}^ + }\) and \(0 \le N \le 7\) , prove that \(N\) can take one of only three possible values.
Answer/Explanation
Markscheme
consider the following
 M1A1A1
M1A1A1
we see that the only possible values so far are \(2\), \(3\) and \(6\) R1
also, the table suggests that these values repeat themselves but we have to prove this
let \(f(n) = {n^2} + 2n + 3\) , consider
\(f(n + 4) – f(n) = {(n + 4)^2} + 2(n + 4) + 3 – {n^2} – 2n – 3\) M1
\( = 8n + 24\) A1
since \(8n + 24\) is divisible by \(8\), M1
\(f(n + 4) \equiv (n)(\bmod 8)\) A1
this confirms that the values do repeat every \(4\) values of \(n\) so that \(2\), \(3\) and \(6\) are the only values taken for all values of \(n\) R1
[9 marks]
Question
(a) Show that the solution to the linear congruence \(ax \equiv b(\bmod p)\), where \(a,{\text{ }}x,{\text{ }}b,{\text{ }}p \in {\mathbb{Z}^ + },{\text{ }}p\) is prime and \(a\), \(p\) are relatively prime, is given by \(x \equiv {a^{p – 2}}b(\bmod p)\).
(b) Consider the congruences
\(7x \equiv 13(\bmod 19)\)
\(2x \equiv 1(\bmod 7)\).
(i) Use the result in (a) to solve the first congruence, giving your answer in the form \(x \equiv k(\bmod 19)\) where \(1 \leqslant k \leqslant 18\).
(ii) Find the set of integers which satisfy both congruences simultaneously.
Answer/Explanation
Markscheme
(a) using Fermat’s little theorem, (M1)
\({a^{p – 1}} \equiv 1(\bmod p)\) A1
multiplying both sides of the congruence by \({a^{p – 2}}\), (M1)
\({a^{p – 1}}x \equiv {a^{p – 2}}b(\bmod p)\) A1
\(x \equiv {a^{p – 2}}b(\bmod p)\) AG
[4 marks]
(b) (i) the solution is
\(x \equiv {7^{17}} \times 13(\bmod 19)\) A1
consider
\({7^3} = 343 \equiv 1(\bmod 19)\) (A1)
Note: Other powers are possible.
therefore
\(x \equiv {\left( {{7^3}} \right)^5} \times {7^2} \times 13(\bmod 19)\) (A1)
\( \equiv {7^2} \times 13(\bmod 19)\) (A1)
\( \equiv 10(\bmod 19)\) A1
(ii) using any method, including trial and error, the solution to the second congruence is given by \(x \equiv 32(\bmod 7)\) (or equivalent) (A1)
a simultaneous solution is \(x = 67\) (or equivalent, eg \(-66\)) A1
the full solution is \(x = 67 + 133N\) (where \(N \in \mathbb{Z}\)) (or equivalent) A1
Note: Do not FT an incorrect answer from (i).
[8 marks]
Question
Show that \({2^n} \equiv {( – 1)^n}(\bmod 3)\), where \(n \in \mathbb{N}\).
Hence show that an integer is divisible by 3 if and only if the difference between the sum of its binary (base 2) digits in even-numbered positions and the sum of its binary digits in odd-numbered positions is divisible by 3.
Express the hexadecimal (base 16) number \({\text{ABB}}{{\text{A}}_{{\text{16}}}}\) in binary.
Answer/Explanation
Markscheme
METHOD 1
\({2^n} = {(3 – 1)^n}\) M1
\( = {3^n} + n{3^{n – 1}}( – 1) + \frac{{n(n – 1)}}{2}{3^{n – 2}}{( – 1)^2} + {\text{ }} \ldots {\text{ }} + {( – 1)^n}\) A1
since all terms apart from the last one are divisible by 3 R1
\({2^n} \equiv {( – 1)^n}(\bmod 3)\) AG
METHOD 2
attempt to reduce the powers of \(2(\bmod 3)\) M1
\({2^0} = 1(\bmod 3);{\text{ }}{2^1} = – 1(\bmod 3);{\text{ }}{2^2} = 1(\bmod 3);{\text{ }}{2^3} = – 1(\bmod 3){\text{ }} \ldots \) A1
since \(1(\bmod 3) \times 2 = – 1(\bmod 3)\) and \( – 1(\bmod 3) \times 2 = 1(\bmod 3)\) the result can be generalized R1
\(2n \equiv {( – 1)^n}(\bmod 3)\) AG
[3 marks]
the binary number \(N = {({a_n}{a_{n – 1}} \ldots {a_2}{a_1}{a_0})_2}\) has numerical value
\({a_0} \times 1 + {a_1} \times 2 + {a_2} \times {2^2} + \ldots + {a_n} \times {2^n}\) A1
\(N = \left( {{a_0} – {a_1} + {a_2} – \ldots {{( – 1)}^n}{a_n}} \right)(\bmod 3)\) M1A1
hence divisibility of \(N\) by 3 coincides with statement of question AG
[3 marks]
\({\text{ABB}}{{\text{A}}_{16}} = 10 \times {16^3} + 11 \times {16^2} + 11 \times 16 + 10 \times 1\) (A1)
\(N = {(1010)_2} \times {2^{12}} + {(1011)_2} \times {2^8} + {(1011)_2} \times {2^4} + {(1010)_2} \times {2^0}\) (M1)(A1)
Note: Award M1 for expressing A and B in binary.
\(N = {(1010101110111010)_2}\) A1
[4 marks]
Question
Consider the linear congruence \(ax \equiv b(\bmod p)\) where \(a,{\text{ }}b \in {\mathbb{Z}^ + },{\text{ }}p\) is a prime and \(\gcd (a,{\text{ }}p) = 1\). Using Fermat’s little theorem, show that \(x \equiv {a^{p – 2}}b(\bmod p)\).
Hence find the smallest value of \(x\) greater than 100 satisfying the linear congruence \(3x \equiv 13(\bmod 19)\).
Answer/Explanation
Markscheme
multiplying both sides by \({a^{p – 2}}\), M1
\({a^{p – 1}}x \equiv {a^{p – 2}}b(\bmod p)\) A1
using \({a^{p – 1}} \equiv 1(\bmod p)\) R1
therefore, \(x \equiv {a^{p – 2}}b(\bmod p)\) AG
[3 marks]
using the above result,
\(x \equiv {3^{17}} \times 13(\bmod 19){\text{ }}\left( { \equiv 16\,7882\,2119(\bmod 19)} \right)\) A1
\( \equiv 17(\bmod 19)\) (M1)A1
\(x = 112\) A1
[4 marks]
Question
The simple connected planar graph \(J\) has the following adjacency table.
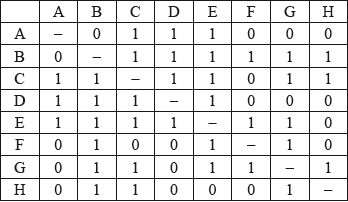
Without attempting to draw \(J\), verify that J satisfies the handshaking lemma;
Without attempting to draw \(J\), determine the number of faces in \(J\).
The vertices D and G are joined by a single edge to form the graph \(K\). Show that \(K\) is not planar.
Explain why a graph containing a cycle of length three cannot be bipartite.
Hence by finding a cycle of length three, show that the complement of \(K\) is not bipartite.
Answer/Explanation
Markscheme
the sum of degrees of the vertices is even (36) or the sum of degrees of the vertices is twice the number of edges A1
[2 marks]
the number of edges \((e)\) is 18 A1
using Euler’s relation \(v – e + f = 2\) M1
\(f = 2 + 18 – 8 = 12\) A1
[2 marks]
if \(K\) is planar then \(e \leqslant 3v – 6\) M1
\(v = 8\) and \(e = 19\) A1
the inequality is not satisfied so \(K\) is not planar A1AG
[3 marks]
let PQRP be a cycle of length 3 in a graph M1
Note: Accept a diagram instead of this statement.
suppose the graph is bipartite
then P must belong to one of the two disjoint sets of vertices and Q, R must belong to the other disjoint set R1
but Q, R cannot belong to the same set because they are linked R1
therefore the graph cannot be bipartite AG
[??? marks]
for example, a suitable cycle of order 3 is AFHA (M1)A1
Note: Award M1 for a valid attempt at drawing the complement or constructing its adjacency table.
[??? marks]

