Question
The acceleration, a ms-2 , of a particle moving in a horizontal line at time t seconds, t ≥ 0 , is given by a = – (1+v) where v ms-1 is the particle’s velocity and v > -1.
At t = 0 , the particle is at a fixed origin O and has initial velocity v0 ms-1 .
(a) By solving an appropriate differential equation, show that the particle’s velocity at time t is given by v ( t ) = (1 + v0) e-t – 1 . [6]
(b) Initially at O, the particle moves in the positive direction until it reaches its maximum displacement from O. The particle then returns to O.
Let s metres represent the particle’s displacement from O and smax its maximum displacement from O.
(i) Show that the time T taken for the particle to reach smax satisfies the equation eT = 1 + v0 .
(ii) By solving an appropriate differential equation and using the result from part (b) (i), find an expression for smax in terms of v0 . [7]
Let v (T – k) represent the particle’s velocity k seconds before it reaches smax , where v (T – k) = (1 + v0) e-(T – k) – 1 .
(c) By using the result to part (b) (i), show that v (T – k) = ek – 1 . [2]
Similarly, let v (T + k) represent the particle’s velocity k seconds after it reaches smax .
(d) Deduce a similar expression for v (T + k) in terms of k . [2]
(e) Hence, show that v (T – k) + v (T + k) ≥ 0 . [3]
Answer/Explanation
Ans:
(a) Since $a=\frac{\text{d}v}{\text{d}t}$, and $a=-\left(1+v\right)$, we have
$$\begin{eqnarray}
\frac{\text{d}v}{\text{d}t} = -1-v \nonumber \\
\frac{\text{d}v}{\text{d}t}+v = -1.
\end{eqnarray}$$
Let $\text{I}\left(x\right)=\text{e}^{\int 1 \text{d}t}=\text{e}^t$.<br>
Then, we have
$$\begin{eqnarray}
\frac{\text{d}}{\text{d}t}\left(v\text{e}^t\right) = -\text{e}^t \nonumber \\
v\text{e}^t = -\int\text{e}^t \text{d}t \nonumber \\
v\text{e}^t = -\text{e}^t+c \nonumber \\
v = c\text{e}^{-t}-1.
\end{eqnarray}$$
Since $v=v_0$ when $t=0$, we have $c=1+v_0$, i.e., $v=\left(1+v_0\right)\text{e}^{-t}-1$.<br>
(b)(i) At $s_{\text{max}}$, $t=T$, i.e., we have
$$\begin{eqnarray}
v\left(T\right) = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T}-1 = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T} = 1 \nonumber \\
1+v_0 = \text{e}^T.
\end{eqnarray}$$
(b)(ii) Since $\frac{\text{d}s}{\text{d}t}=\left(1+v_0\right)\text{e}^{-t}-1$, integrating both sides with respect to $t$, we have
$$\begin{eqnarray}
s &=& \int\left(1+v_0\right)\text{e}^{-t}-1\text{d}t \nonumber \\
&=& -\left(1+v_0\right)\text{e}^{-t}-t+c.
\end{eqnarray}$$
When $t=0$, $s=0$, i.e.,
$$\begin{eqnarray}
0 = -\left(1+v_0\right)+c \nonumber \\
c = \left(1+v_0\right).
\end{eqnarray}$$
Thus, $s=\left(1+v_0\right)-\left(1+v_0\right)\text{e}^{-t}-t$.<br>
Since from (b)(i) we have $1+v_0=\text{e}^T$, $T=\ln\left(1+v_0\right)$, i.e., $s_{\text{max}}=v_0-\ln \left(1+v_0\right)$.<br>
(c) Since $\text{e}^T=1+v_0$, we have $\left(1+v_0\right)\text{e}^{-T}=1$, i.e.,
$$\begin{eqnarray}
v\left(T-k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T-k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^k-1 \nonumber \\
&=& \text{e}^k-1.
\end{eqnarray}$$
(d) Similarly, as in (c),
$$\begin{eqnarray}
v\left(T+k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T+k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^{-k}-1.
\end{eqnarray}$$
(e)
$$\begin{eqnarray}
v\left(T-k\right)+v\left(T+k\right) &=& \text{e}^k-1+\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^k+\text{e}^{-k}-2 \nonumber \\
&=& \frac{\text{e}^{2k}-2\text{e}^k+1}{\text{e}^k} \nonumber \\
&=& \frac{\left(\text{e}^k-1\right)^2}{\text{e}^k} \geq 0.
\end{eqnarray}$$
Question
Find \(\int {(1 + {{\tan }^2}x){\text{d}}x} \).[2]
Find \(\int {{{\sin }^2}x{\text{d}}x} \).[3]
Answer/Explanation
Markscheme
\(\int {(1 + {{\tan }^2}x){\text{d}}x} = \int {{{\sec }^2}x{\text{d}}x = \tan x( + c)} \) M1A1
[2 marks]
\(\int {{{\sin }^2}x{\text{d}}x} = \int {\frac{{1 – \cos 2x}}{2}{\text{d}}x} \) M1A1
\( = \frac{x}{2} – \frac{{\sin 2x}}{4}( + c)\) A1
Note: Allow integration by parts followed by trig identity.
Award M1 for parts, A1 for trig identity, A1 final answer.
[3 marks]
Total [5 marks]
Question
A function \(f\) is defined by \(f(x) = \frac{{3x – 2}}{{2x – 1}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne \frac{1}{2}\).
Find an expression for \({f^{ – 1}}(x)\).[4]
Given that \(f(x)\) can be written in the form \(f(x) = A + \frac{B}{{2x – 1}}\), find the values of the constants \(A\) and \(B\).[2]
Hence, write down \(\int {\frac{{3x – 2}}{{2x – 1}}} {\text{d}}x\).[1]
Answer/Explanation
Markscheme
\(f:x \to y = \frac{{3x – 2}}{{2x – 1}}\;\;\;{f^{ – 1}}:y \to x\)
\(y = \frac{{3x – 2}}{{2x – 1}} \Rightarrow 3x – 2 = 2xy – y\) M1
\( \Rightarrow 3x – 2xy = – y + 2\) M1
\(x(3 – 2y) = 2 – y\)
\(x = \frac{{2 – y}}{{3 – 2y}}\) A1
\(\left( {{f^{ – 1}}(y) = \frac{{2 – y}}{{3 – 2y}}} \right)\)
\({f^{ – 1}}(x) = \frac{{2 – x}}{{3 – 2x}}\;\;\;\left( {x \ne \frac{3}{2}} \right)\) A1
Note: \(x\) and \(y\) might be interchanged earlier.
Note: First M1 is for interchange of variables second M1 for manipulation
Note: Final answer must be a function of \(x\)
[4 marks]
\(\frac{{3x – 2}}{{2x – 1}} = A + \frac{B}{{2x – 1}} \Rightarrow 3x – 2 = A(2x – 1) + B\)
equating coefficients \(3 = 2A\) and \( – 2 = – A + B\) (M1)
\(A = \frac{3}{2}\) and \(B = – \frac{1}{2}\) A1
Note: Could also be done by division or substitution of values.
[2 marks]
\(\int {f(x){\text{d}}x = \frac{3}{2}x – \frac{1}{4}\ln \left| {2x – 1} \right| + c} \) A1
Note: accept equivalent e.g. \(\ln \left| {4x – 2} \right|\)
[1 mark]
Total [7 marks]
Question
- Find \(\int_{0}^{2}\frac{1}{4+x^2}dx\)
- Find \(k\) given that \(\int_{0}^{k}\frac{1}{4+x^2}dx=\frac{\pi}{6}\)
Answer/Explanation
Ans:
- \(\frac{\pi}{8}\)
- \(k=2\sqrt{3}\)
Question
Find the real number \(k>1\) for which \(\int_{1}^{k}dx=\frac{3}{2}\).
Answer/Explanation
Ans:
\(\int_{1}^{k}(1+\frac{1}{x^2})dx=\frac{3}{2}\left[ x-\frac{1}{x} \right]_1^k=\frac{3}{2}\)
\(k-\frac{1}{k}=\frac{3}{2}\)⇒\(2k^2-3k-2=0\)⇒ \((2k+1)(k-2)=0\)
\(k=2\) since \(k>1\)
Question
- Find \(\int_{0}^{m}\frac{dx}{2x+3},\) giving your answer in terms of \(m\).
- Given that \(\int_{0}^{m}\frac{dx}{2x+3}=1,\) calculate the value of \(m\).
Answer/Explanation
Ans:
- Given that \(\int_{0}^{m}\frac{dx}{2x+3}=1,\) calculate the value of \(m\).
\(\int_{0}^{m}\frac{dx}{2x+3}=\left[ \frac{1}{2} ln|2x+3| \right]_0^m\)
\(=\frac{1}{2}ln|\frac{2m+3}{3}| \left( or \frac{1}{2} \space ln|2m+3|-\frac{1}{2}ln \space 3 \right)\)
Note: Modulus signs are not required. - \(\frac{1}{2}ln|\frac{2m+3}{3}|=1\)
\(|\frac{2m+3}{3}|=e^2, \left( \frac{2m+3}{3}=\pm 3^2, \space negative \space sign \space not \space required \right)\)
\(\frac{2m+3}{3}=e^2\)⇒\(\frac{2m}{3}=e^2-1\)
\(m=\frac{3}{2}(e^2-1)=(=9.58)\)
Note: Do not penalize if a candidate has also obtained the incorrect value \(m = –12.6\)
Question
Find the values of \(a>0\), such that \(\int_{a}^{a^2} \frac{1}{1+x^2}dx=0.22\).
Answer/Explanation
Ans:
If \(\int_{a}^{a^2} \frac{1}{1+x^2}dx=0.22\)
Then \(\left[\arctan x \right]_a^{a^2}=0.22\)
\(\arctan a^2- \arctan a -0.22=0\)
\(a=2.04\) or \(a=2.62\)
Question
Find the value of \(a\) such that \(\int_{0}^{a} cos^2 x dx = 0.740.\) Give your anwer to 3 decimal places.
Answer/Explanation
Ans:
\(\int_{0}^{a}cos^2 x dx = 0.740\)
⇒\(\frac{1}{2}\int_{0}^{a}(cos2x+1)dx=0.740\)(using formulae and statistical tables)
⇒\(\frac{1}{2}\left[\frac{1}{2}sin2x+x \right]_0^a=0.740\)
⇒\(sin(2a)+2a-2.960=0\)
⇒\(a=1.047\)(using a graphic display calculator)
Question
The diagram below shows the graph of \(y_1=f(x),0 \le x \le 4\)
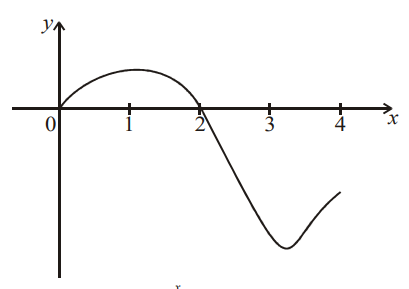
On the axes below, sketch the graph of \(y_2=\int_{0}^{x}f(t)dt,\) marking clearly the points of inflexion.
HINT: The fundamental theorem of Calculus says that the derivative of \(\int_{0}^{x} f(t)dt\) is \(f(x)\).
Answer/Explanation
Ans:
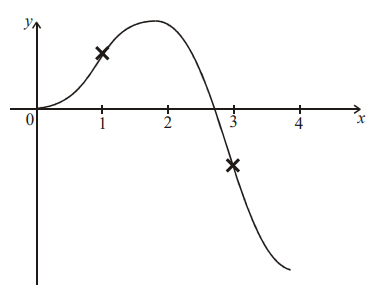
Question
Find \(\int_{0}^{ln3} \frac{e^x}{e^{2x}+9}dx,\) expressing your answer in exact form.
Answer/Explanation
Ans:
Let \(u=e^x\)
\(du=e^x dx\)(or equivalent)
When \(x=0,u=1\) and when \(x=ln3,u=3\)
\(\int_{0}^{ln3}\frac{e^x}{e^{2x}+9}dx=\int_{1}^{3}\frac{1}{u^2+9}du\)
\(=\frac{1}{3} \left[ \arctan \frac{u}{3} \right]_1^3\)
\(=\frac{1}{3} \left( \arctan 1 – \arctan \frac{1}{3} \right) \left( =\frac{\pi}{12}-\frac{1}{3}\arctan \frac{1}{3}, \frac{1}{3} \arctan \frac{1}{2} \right)\)
[MAI 5.14-5.15] MORE INTEGRALS – SUBSTITUTION-manav
Question
[Maximum mark: 18]
Find the following integrals

Answer/Explanation
ans:

Question
[Maximum mark: 27]
Find the following integrals (modify the expressions first, if necessary).

Answer/Explanation
ans:

Question
[Maximum mark: 30]
Find the following integrals

Answer/Explanation
ans:

Question
[Maximum mark: 21]
Find the following integrals

Answer/Explanation
ans:

Question
[Maximum mark: 21]
Find the following integrals

Answer/Explanation
ans:

Question
[Maximum mark: 6]
Let $f(x)=\sqrt{x^{1}}$. Find
(a) $r^{*}(x)^{-}$ [3]
(b) $\int f(x) a r .$ [3]
Answer/Explanation
ans:
\(
f(x)=x^{\frac{3}{2}}
\)
\(
\text { (a) } \left.f^{\prime}(x)=\frac{3}{2} x^{\frac{3}{2}-1}=\frac{3}{2} x^{\frac{1}{2}} \text { (or } \frac{3}{2} \sqrt{x}\right)
\)
\(
\text { (b) } \int x^{\frac{3}{2}} \mathrm{~d} x=\frac{1}{\frac{3}{2}+1} x^{\frac{3}{2}+1}+c=\frac{2}{5} x^{\frac{5}{2}}+c \text { (or } \frac{2}{5} \sqrt{x^{5}}+c \text { ) }
\)
Question
[Maximum mark: 6]
Find
\(
\text { (a) } \int \sin (3 x+7) d x \text {; }
\) [2]
\(
\text { (b) } \int e^{-4 x} d x \text {. }
\) [2]
\(
\text { (c) } \int \cos (1-x) d x
\) [2]
Answer/Explanation
ans:
(a) $\int \sin (3 x+7) \mathrm{d} x=-\frac{1}{3} \cos (3 x+7)+C$
(b) $\int \mathrm{e}^{-4 x} \mathrm{~d} x=-\frac{1}{4} \mathrm{e}^{-4 x}+C$
(c) $\int \cos (1-x) \mathrm{d} x=-\sin (1-x)+C$
Question
[Maximum mark: 6]
\(
\text { The function } f \text { is given by } f(x)=2 \sin (5 x-3) \text {. }
\)
\(
\text { (a) Find } f^{\prime \prime}(x) \text {. }
\) [4]
\(
\text { (b) Write down } \int f(x) \mathrm{d} x \text {. }
\) [2]
Answer/Explanation
ans:
\(
\text { (a) } f^{\prime}(x)=(2 \cos (5 x-3)) 5(=10 \cos (5 x-3))
\)
\(
\text { (b) } \quad \int f(x) \mathrm{d} x=\frac{2}{5} \cos (5 x-3)+c
\)
Question
[Maximum mark: 6]
\(
\text { Let } f(x)=(3 x+4)^{3} \text {. Find }
\)
\(
\text { (i) } f^{\prime}(x) \text {; }
\)
\(
\text { (ii) } \int f(x) d x \text {. }
\)
Answer/Explanation
ans:
\(
\text { (i) } f^{\prime}(x)=5(3 x+4)^{4} \times 3\left(=15(3 x+4)^{4}\right)
\)
\(
\text { (ii) } \int(3 x+4)^{5} \mathrm{~d} x=\frac{1}{3} \times \frac{1}{6}(3 x+4)^{6}+c\left(=\frac{(3 x+4)^{6}}{18}+c\right)
\)
Question
[Maximum mark: 6]
\(
\text { Given that } f(x)=(2 x+5)^{3} \text { find }
\)
\(
\text { (i) } f^{\prime}(x) \text {; }
\)
\(
\text { (ii) } \int f(x) \mathrm{d} x \text {. }
\)
Answer/Explanation
ans:
\(
\text { (i) } f^{\prime}(x)=3(2 x+5)^{2} \times 2=6(2 x+5)^{2}
\)
\(
\text { (ii) } \quad \int f(x) \mathrm{d} x=\frac{(2 x+5)^{4}}{4 \times 2}+c
\)
Question
[Maximum mark: 4]
\(
\text { If } f^{\prime}(x)=\cos x \text {, and } f\left(\frac{\pi}{2}\right)=-2 \text {, find } f(x) \text {. }
\)
Answer/Explanation
ans:
\(
\begin{aligned}
&f^{\prime}(x)=\cos x \Rightarrow f(x)=\sin x+C \\
&f\left(\frac{\pi}{2}\right)=-2 \Rightarrow-2=\sin \left(\frac{\pi}{2}\right)+C \Rightarrow C=-3 \\
&f(x)=\sin x-3
\end{aligned}
\)
Question
[Maximum mark: 7]
\(
\text { A gradient function is given by } \frac{\mathrm{d} y}{\mathrm{~d} x}=10 \mathrm{e}^{2 x}-5 \text {. When } x=0, y=8 \text {. Find the value of } y
\)
\(
\text { when } x=1 \text {. }
\)
Answer/Explanation
ans:
\(
y=5 \mathrm{e}^{2 x}-5 x+C
\)
\(
\text { substituting }(0,8): 8=5+C \Rightarrow C=3
\)
\(
y=5 \mathrm{e}^{2 x}-5 x+3
\)
\(
\text { substituting } x=1
\)
\(
y=5 \mathrm{e}^{2}-2 \quad(=34.9)
\)
Question
[Maximum mark: 6]
\(
\text { The derivative of the function } f \text { is given by } f^{\prime}(x)=\frac{1}{1+x}-0.5 \sin x \text {, for } x \neq-1 \text {. }
\)
\(
\text { The graph of } f \text { passes through the point }(0,2) \text {. Find an expression for } f(x) \text {. }
\)
Answer/Explanation
ans:
\(
\begin{aligned}
&f(x)=\int\left(\frac{1}{x+1}-0.5 \sin x\right) \mathrm{d} x=\ln (x+1)+0.5 \cos x+c \\
&2=\ln 1+0.5+c \Rightarrow c=1.5 \\
&f(x)=\ln (x+1)+0.5 \cos x+1.5
\end{aligned}
\)
Question
[Maximum mark: 6]
\(
\text { The derivative of the function } f \text { is given by } f^{\prime}(x)=e^{-2 x}+\frac{1}{1-x}, x<1 \text {. }
\)
\(
\text { The graph of } y=f(x) \text { passes through the point }(0,4) \text {. Find an expression for } f(x) \text {. }
\)
Answer/Explanation
ans:
\(
\begin{aligned}
&f(x)=\int \sin (2 x-3) \mathrm{d} x=-\frac{1}{2} \cos (2 x-3)+C \\
&\text { initial condition: } \quad 4=-\frac{1}{2} \cos 0+C \Rightarrow C=4.5 \\
&f(x)=-\frac{1}{2} \cos (2 x-3)+4.5
\end{aligned}
\)
Question
[Maximum mark: 6]
\(
\text { The graph of the function } y=f(x) \text { passes through the point }\left(\frac{3}{2}, 4\right) \text {. The gradient }
\)
\(
\text { function of } f \text { is given as } f^{\prime}(x)=\sin (2 x-3) \text {. Find } f(x) \text {. }
\)
Answer/Explanation
ans:
\(
\begin{aligned}
&f(x)=\int \sin (2 x-3) \mathrm{d} x=-\frac{1}{2} \cos (2 x-3)+C \\
&\text { initial condition: } 4=-\frac{1}{2} \cos 0+C \Rightarrow C=4.5 \\
&f(x)=-\frac{1}{2} \cos (2 x-3)+4.5
\end{aligned}
\)
Question
[Maximum mark: 8]
Find
\(
\text { (i) Find } \int \frac{1}{2 x+3} \mathrm{~d} x \text {. }
\)
\(
\text { (ii) } \int \frac{1}{(2 x+3)^{2}} d x
\)
\(
\text { (iii) } \int \frac{1}{(2 x+3)^{3}} d x
\)
Answer/Explanation
ans:
\(
\text { (a) } \int \frac{1}{2 x+3} \mathrm{~d} x=\frac{1}{2} \operatorname{In}(2 x+3)+C
\)
\(
\text { (b) } \int \frac{1}{(2 x+3)^{2}} d x=\int(2 x+3)^{-2} d x=\frac{1}{2} \frac{(2 x+3)^{-1}}{-1}+C=-\frac{1}{4 x+6}+C
\)
\(
\text { (c) } \int \frac{1}{(2 x+3)^{3}} d x=\int(2 x+3)^{-3} d x=\frac{1}{2} \frac{(2 x+3)^{-2}}{-2}+C=-\frac{1}{4(2 x+3)^{2}}+C
\)
Question
[Maximum mark: 6]
\(
\text { Find } \int \frac{6}{2 x-3} d x
\)
(i) directly by inspection
(ii) by using the substitution u = 2x – 3
Answer/Explanation
ans:
SUBSTITUTION
\(
\text { (i) } \int \frac{6}{2 x-3} d x=3 \ln (2 x-3)+c
\)\
\(
\text { (ii) } u=2 x-3 \Rightarrow \frac{d u}{d x}=2 \Rightarrow d x=\frac{d u}{2} \text {. Thus } \int \frac{6}{u} \frac{d u}{2}=3 \int \frac{1}{u} d u=3 \ln u+c=3 \ln (2 x-3)+c
\)
Question
[Maximum mark: 5]
\(
\text { Find } \int \frac{6 x}{2 x^{2}-3} d x \text {, by using the substitution } u=2 x^{2}-3
\)
Answer/Explanation
ans:
\(
\int \frac{6 x}{2 x^{2}-3} d x . \quad u=2 x^{2}-3 \Rightarrow \frac{d u}{d x}=4 x \Rightarrow d x=\frac{d u}{4 x}
\)
\(
\text { (ii) } u=2 x-3 \Rightarrow \frac{d u}{d x}=2 \Rightarrow d x=\frac{d u}{2} \text {. Thus } \int \frac{6}{u} \frac{d u}{2}=3 \int \frac{1}{u} d u=3 \ln u+c=3 \ln (2 x-3)+c
\)
Question
[Maximum mark: 9]
Find
\(
\text { (i) } \int 6 e^{3 x+7} d x
\)
\(
\text { (ii) } \int 6 x e^{3 x^{2}+7} d x
\)
\(
\text { (iii) } \int 6 x^{2} e^{3 x^{2}+7} d x
\)
Answer/Explanation
ans:
In the following questions only the final answers are given and the corresponding substitutions
\(
\text { (i) } \int 6 e^{3 x+7} d x=2 e^{3 x+7} \quad(u=3 x+7)
\)
\(
\text { (ii) } \int 6 x e^{3 x^{2}+7} d x=e^{3 x^{2}+7}\left(u=3 x^{2}+7\right)
\)
\(
\text { (iii) } \int 6 x^{2} e^{3 x^{3}+7} d x=\frac{2}{3} e^{3 x^{3}+7} \quad\left(u=3 x^{3}+7\right)
\)
Question
[Maximum mark: 8]
Find
\(
\text { (i) } \int 3 x \sin \left(x^{2}+1\right) d x
\)
\(
\text { (ii) } \int 3 x^{2} \cos \left(x^{3}+1\right) d x
\)
Answer/Explanation
ans:
\(
\text { (i) } \int 3 x \sin \left(x^{2}+1\right) d x=-\frac{3}{2} \cos \left(x^{2}+1\right) \quad\left(u=x^{2}+1\right)
\)
\(
\text { (ii) } \int 3 x^{2} \cos \left(x^{3}+1\right) d x=\sin \left(x^{3}+1\right)
\)
\(
\left(u=x^{3}+1\right)
\)
Question
[Maximum mark: 5
\(
\text { Find } \quad \int \frac{3 x^{2}}{x^{3}+1} d x
\)
Answer/Explanation
ans;
\(
\int \frac{3 x^{2}}{x^{3}+1} d x=\ln \left(x^{3}+1\right) \quad\left(u=x^{3}+1\right)
\)
Question
[Maximum mark: 5]
\(
\text { Find } \int \frac{(\ln x)^{5}}{x} d x
\)
Answer/Explanation
ans:
\(
\int \frac{(\ln x)^{5}}{x} d x=\frac{(\ln x)^{6}}{6}+c \quad(u=\ln x)
\)
Question
[Maximum mark: 5]
\(
\text { Find } \int \frac{\tan ^{5} x}{\cos ^{2} x} d x
\)
Answer/Explanation
ans:
\(
\int \frac{\tan ^{5} x}{\cos ^{2} x} d x=\frac{\tan ^{6} x}{6}+c \quad(u=\tan x)
\)
Question
[Maximum mark: 20]
Calculate the following definite integrals

Answer/Explanation
ans:
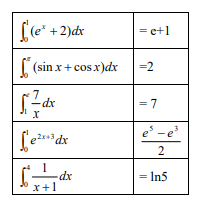
Question
[Maximum mark: 6]
\(
\text { Let } f(x)=x \ln x-x
\)
\(
\text { (a) Find } f^{\prime}(x)
\)
\(
\text { (a) Find } f^{\prime}(x)
\) [3]
\(
\text { (b) Hence find the exact value of } \int_{1}^{3} \ln x d x \text {. }
\) [3]
Answer/Explanation
ans:
\(
\text { (a) } f^{\prime}(x)=\ln x
\)
\(
\text { (b) } 3 \ln 3-2
\)
Question
[Maximum mark: 6]
\(
\text { (a) Find } \int \frac{1}{2 x+3} \mathrm{~d} x \text {. }
\) [2]
\(
\text { (b) Given that } \int_{0}^{3} \frac{1}{2 x+3} \mathrm{~d} x=\ln \sqrt{P} \text {, find the value of } P \text {. }
\) [2]
Answer/Explanation
ans:
Question
\text { Given } \int_{3}^{k} \frac{1}{x-2} d x=\ln 7 \text {, find the value of } k \text {. }
\)
Answer/Explanation
\begin{aligned}
&\int_{3}^{k} \frac{1}{x-2} \mathrm{~d} x=[\ln (x-2)]_{3}^{k}=\ln (k-2)-\ln 1 \\
&\ln (\mathrm{k}-2)-\ln 1=\ln 7 \Rightarrow k-2=7, \text { thus } \mathrm{k}=9
\end{aligned}
\)
Question
\text { Let } \int_{5}^{7} f(x) d x=8 \text {. Find the values of the following expressions }
\)

Answer/Explanation

Question
\int_{c}^{d} f(x-2) \mathrm{d} x=8
\). write down the value of c and of d. [2]
\int_{4}^{b} f(2 x) d x=4.
\) write down the value of a and of b. [2]
\int_{0}^{3}\left(f(x)+e^{x}\right) d x. [3]
\)
Answer/Explanation
\text { (a) } \quad \int_{c}^{d} f(x-2) \mathrm{d} x=8, c=2, d=5
\)
\text { (b) } \quad \int_{a}^{b} f(2 x) d x=4, \quad a=0, b=1.5
\)
\text { (c) } \quad \int_{0}^{3}\left(f(x)+e^{x}\right) d x=\int_{0}^{3} f(x) d x \int_{0}^{3} e^{x} d x=8+e^{3}-1=7+e^{3}
\)
Question
\text { (i) } \int 2 \sqrt{x+3} d x
\)
\text { (ii) } \int 2 x \sqrt{x^{2}+3} d x
\)
\text { (iii) } \int 2 x^{2} \sqrt{x^{3}+3} d x
\)
Answer/Explanation
\text { (i) } \int 2 \sqrt{x+3} d x=\frac{4}{3}(x+3)^{3 / 2}
\) \(
(u=x+3)
\)
\text { (ii) } \int 2 x \sqrt{x^{2}+3} d x=\frac{2}{3}\left(x^{2}+3\right)^{3 / 2}
\) \(
\left(u=x^{2}+3\right)
\)
\text { (iii) } \int 2 x^{2} \sqrt{x^{3}+3} d x=\frac{4}{9}\left(x^{3}+3\right)^{3 / 2}
\) \(
\left(u=x^{3}+3\right)
\)
Question
A=\int \cos x e^{\sin x} d x, \quad B=\int \cos x \sqrt{\sin x} d x, \quad C=\int \sin ^{2} x \cos x d x, \quad D=\int \cos ^{3} x \sin x d x
\)
Answer/Explanation
\begin{array}{ll}
A=\int \cos x e^{\sin x} d x=e^{\sin x} & (u=\sin x) \\
B=\int \cos x \sqrt{\sin x} d x=\frac{2}{3}(\sin x)^{3 / 2} & (u=\sin x) \\
C=\int \sin ^{2} x \cos x d x=\frac{\sin ^{3} x}{3}+c & (u=\sin x) \\
D=\int \cos ^{3} x \sin x d x=-\frac{\cos ^{3} x}{3}+c & (u=\cos x)
\end{array}
\)
Question
\text { (a) } \int \frac{2 x+\cos x}{x^{2}+\sin x} d x
\) [2]
\text { (b) } \quad \int e^{x} \sqrt{e^{x}+1} d x
\) [4]
\text { (c) } \quad \int\left(3 x^{2}+\cos x\right)\left(x^{3}+\sin x\right)^{3} d x
\) [4]
Answer/Explanation
\text { (i) } \int \frac{2 x+\cos x}{x^{2}+\sin x} d x=\ln \left(x^{2}+\sin x\right) \quad\left(u=x^{2}+\sin x\right)
\)
\text { (ii) } \int e^{x} \sqrt{e^{x}+1} d x=\frac{2}{3}\left(e^{x}+1\right)^{3 / 2} \quad\left(u=e^{x}+1\right)
\)
Question
u=\ln x
\) ln to find the integrals
\text { (i) } \int \frac{(\ln x)^{2}}{x} d x
\)
\text { (ii) } \int \frac{\sqrt{\ln x}}{x} d x
\)
\text { (iii) } \int \frac{1}{x(\ln x)^{2}} d x
\)
\text { (iv) } \int \frac{\ln x}{x} d x
\)
Answer/Explanation
\text { (i) } \int \frac{(\ln x)^{2}}{x} d x=\frac{(\ln x)^{3}}{3}+c
\)
\text { (ii) } \int \frac{\sqrt{\ln x}}{x} d x=\frac{2}{3}(\ln x)^{\frac{3}{2}}+c
\)
\text { (iii) } \int \frac{1}{x(\ln x)^{2}} d x=-(\ln x)^{-1}+c=-\frac{1}{\ln x}+c
\)
\text { (iv) } \int \frac{\ln x}{x} d x=\frac{(\ln x)^{2}}{2}+c
\)
