Question
Consider the vectors a \( = \sin (2\alpha )\)i \( – \cos (2\alpha )\)j + k and b \( = \cos \alpha \)i \( – \sin \alpha \)j − k, where \(0 < \alpha < 2\pi \).
Let \(\theta \) be the angle between the vectors a and b.
(a) Express \(\cos \theta \) in terms of \(\alpha \).
(b) Find the acute angle \(\alpha \) for which the two vectors are perpendicular.
(c) For \(\alpha = \frac{{7\pi }}{6}\), determine the vector product of a and b and comment on the geometrical significance of this result.
▶️Answer/Explanation
Markscheme
(a) \(\cos \theta = \frac{{\boldsymbol{ab}}}{{\left| \boldsymbol{a} \right|\left| \boldsymbol{b} \right|}} = \frac{{\sin 2\alpha \cos \alpha + \sin \alpha \cos 2\alpha – 1}}{{\sqrt 2 \times \sqrt 2 }}{\text{ }}\left( { = \frac{{\sin 3\alpha – 1}}{2}} \right)\) M1A1
(b) \({\boldsymbol{a}} \bot {\boldsymbol{b}} \Rightarrow \cos \theta = 0\) M1
\(\sin 2\alpha \cos \alpha + \sin \alpha \cos 2\alpha – 1 = 0\)
\(\alpha = 0.524{\text{ }}\left( { = \frac{\pi }{6}} \right)\) A1
(c)
METHOD 1
\(\left| {\begin{array}{*{20}{c}}
{\boldsymbol{i}}&{\boldsymbol{j}}&{\boldsymbol{k}} \\
{\sin 2\alpha }&{ – \cos 2\alpha }&1 \\
{\cos \alpha }&{ – \sin \alpha }&{ – 1}
\end{array}} \right|\) (M1)
assuming \(\alpha = \frac{{7\pi }}{6}\)
Note: Allow substitution at any stage.
\(\left| {\begin{array}{*{20}{c}}
\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k} \\
{\frac{{\sqrt 3 }}{2}}&{ – \frac{1}{2}}&1 \\
{ – \frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}&{ – 1}
\end{array}} \right|\) A1
\(= \boldsymbol{i} \left( {\frac{1}{2} – \frac{1}{2}} \right) – \boldsymbol{j} \left( { – \frac{{\sqrt 3 }}{2} + \frac{{\sqrt 3 }}{2}} \right) + \boldsymbol{k}\left( {\frac{{\sqrt 3 }}{2} \times \frac{1}{2} – \frac{1}{2} \times \frac{{\sqrt 3 }}{2}} \right)\)
= 0 A1
a and b are parallel R1
Note: Accept decimal equivalents.
METHOD 2
from (a) \(\cos \theta = – 1{\text{ (and }}\sin \theta = 0)\) M1A1
\(\boldsymbol{a} \times \boldsymbol{b}\) = 0 A1
a and b are parallel R1
[8 marks]
Examiners report
This question was attempted by most candidates who in general were able to find the dot product of the vectors in part (a). However the simplification of the expression caused difficulties which affected the performance in part (b). Many candidates had difficulties in interpreting the meaning of a \( \times \) b = 0 in part (c).
Question
The diagram shows a cube OABCDEFG.
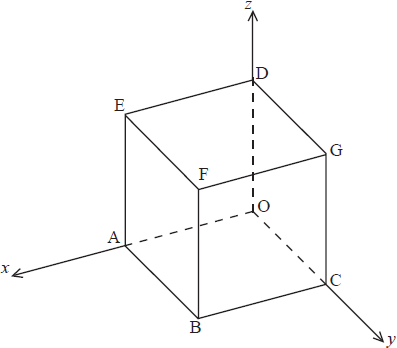
Let O be the origin, (OA) the x-axis, (OC) the y-axis and (OD) the z-axis.
Let M, N and P be the midpoints of [FG], [DG] and [CG], respectively.
The coordinates of F are (2, 2, 2).
(a) Find the position vectors \(\overrightarrow {{\text{OM}}} \), \(\overrightarrow {{\text{ON}}} \) and \(\overrightarrow {{\text{OP}}} \) in component form.
(b) Find \(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} \).
(c) Hence,
(i) calculate the area of the triangle MNP;
(ii) show that the line (AG) is perpendicular to the plane MNP;
(iii) find the equation of the plane MNP.
(d) Determine the coordinates of the point where the line (AG) meets the plane MNP.
▶️Answer/Explanation
Markscheme
(a) \(\overrightarrow {{\text{OM}}} = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
2
\end{array}} \right)\), \(\overrightarrow {{\text{ON}}} = \left( {\begin{array}{*{20}{c}}
0 \\
1 \\
2
\end{array}} \right)\) and \(\overrightarrow {{\text{OP}}} = \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
1
\end{array}} \right)\) A1A1A1
[3 marks]
(b) \(\overrightarrow {{\text{MP}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
0 \\
{ – 1}
\end{array}} \right)\) and \(\overrightarrow {{\text{MN}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 1} \\
0
\end{array}} \right)\) A1A1
\(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} = \left( {\begin{array}{*{20}{c}}
i&j&k \\
{ – 1}&0&{ – 1} \\
{ – 1}&{ – 1}&0
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)\) (M1)A1
[4 marks]
(c) (i) area of MNP \( = \frac{1}{2}\left| {\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} } \right|\) M1
\( = \frac{1}{2}\left| {\left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)} \right|\)
\( = \frac{{\sqrt 3 }}{2}\) A1
(ii) \(\overrightarrow {{\text{OA}}} = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right)\), \(\overrightarrow {{\text{OG}}} = \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
2
\end{array}} \right)\)
\(\overrightarrow {{\text{AG}}} = \left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) A1
since \(\overrightarrow {{\text{AG}}} = 2(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} )\) AG is perpendicular to MNP R1
(iii) \(r \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
2
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)\) M1A1
\(r \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = 3\) (accept \( – x + y + z = 3\)) A1
[7 marks]
(d) \(r = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) A1
\(\left( {\begin{array}{*{20}{c}}
{2 – 2\lambda } \\
{2\lambda } \\
{2\lambda }
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = 3\) M1A1
\( – 2 + 2\lambda + 2\lambda + 2\lambda = 3\)
\(\lambda = \frac{5}{6}\) A1
\(r = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right) + \frac{5}{6}\left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) M1
coordinates of point \(\left( {\frac{1}{3},\frac{5}{3},\frac{5}{3}} \right)\) A1
[6 marks]
Total [20 marks]
Examiners report
This was the most successfully answered question in part B, with many candidates achieving full marks. There were a few candidates who misread the question and treated the cube as a unit cube. The most common errors were either algebraic or arithmetic mistakes. A variety of notation forms were seen but in general were used consistently. In a few cases, candidates failed to show all the work or set it properly.
Question
The points P(−1, 2, − 3), Q(−2, 1, 0), R(0, 5, 1) and S form a parallelogram, where S is diagonally opposite Q.
Find the coordinates of S.[2]
The vector product \(\overrightarrow {{\text{PQ}}} \times \overrightarrow {{\text{PS}}} = \left( {\begin{array}{*{20}{c}}
{ – 13} \\
7 \\
m
\end{array}} \right)\). Find the value of m .[2]
Hence calculate the area of parallelogram PQRS.[2]
Find the Cartesian equation of the plane, \({\prod _1}\) , containing the parallelogram PQRS.[3]
Write down the vector equation of the line through the origin (0, 0, 0) that is perpendicular to the plane \({\prod _1}\) .[1]
Hence find the point on the plane that is closest to the origin.[3]
A second plane, \({\prod _2}\) , has equation x − 2y + z = 3. Calculate the angle between the two planes.[4]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\text{PQ}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 1} \\
3
\end{array}} \right)\) , \(\overrightarrow {{\text{SR}}} = \left( {\begin{array}{*{20}{c}}
{0 – x} \\
{5 – y} \\
{1 – z}
\end{array}} \right)\) (M1)
point S = (1, 6, −2) A1
[2 marks]
\(\overrightarrow {{\text{PQ}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 1} \\
3
\end{array}} \right)\)\(\overrightarrow {{\text{PS}}} = \left( {\begin{array}{*{20}{c}}
2 \\
4 \\
1
\end{array}} \right)\) A1
\(\overrightarrow {{\text{PQ}}} \times \overrightarrow {{\text{PS}}} = \left( {\begin{array}{*{20}{c}}
{ – 13} \\
7 \\
{ – 2}
\end{array}} \right)\)
m = −2 A1
[2 marks]
area of parallelogram PQRS \( = \left| {\overrightarrow {{\text{PQ}}} \times \overrightarrow {{\text{PS}}} } \right| = \sqrt {{{( – 13)}^2} + {7^2} + {{( – 2)}^2}} \) M1
\( = \sqrt {222} = 14.9\) A1
[2 marks]
equation of plane is −13x + 7y − 2z = d M1A1
substituting any of the points given gives d = 33
−13x + 7y − 2z = 33 A1
[3 marks]
equation of line is \(\boldsymbol{r} = \left( {\begin{array}{*{20}{c}}
0 \\
0 \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
{ – 13} \\
7 \\
{ – 2}
\end{array}} \right)\) A1
Note: To get the A1 must have \(\boldsymbol{r} =\) or equivalent.
[1 mark]
\(169\lambda + 49\lambda + 4\lambda = 33\) M1
\(\lambda = \frac{{33}}{{222}}{\text{ }}( = 0.149…)\) A1
closest point is \(\left( { – \frac{{143}}{{74}},\frac{{77}}{{74}}, – \frac{{11}}{{37}}} \right){\text{ }}\left( { = ( – 1.93,{\text{ 1.04, – 0.297)}}} \right)\) A1
[3 marks]
angle between planes is the same as the angle between the normals (R1)
\(\cos \theta = \frac{{ – 13 \times 1 + 7 \times – 2 – 2 \times 1}}{{\sqrt {222} \times \sqrt 6 }}\) M1A1
\(\theta = 143^\circ \) (accept \(\theta = 37.4^\circ \) or 2.49 radians or 0.652 radians) A1
[4 marks]
Examiners report
This was a multi-part question that was well answered by many candidates. Wrong answers to part (a) were mainly the result of failing to draw a diagram. Follow through benefitted many candidates. A high proportion of candidates lost the mark in (e) by not writing their answer as an equation in the form r = …
This was a multi-part question that was well answered by many candidates. Wrong answers to part (a) were mainly the result of failing to draw a diagram. Follow through benefitted many candidates. A high proportion of candidates lost the mark in (e) by not writing their answer as an equation in the form r = …
This was a multi-part question that was well answered by many candidates. Wrong answers to part (a) were mainly the result of failing to draw a diagram. Follow through benefitted many candidates. A high proportion of candidates lost the mark in (e) by not writing their answer as an equation in the form r = …
This was a multi-part question that was well answered by many candidates. Wrong answers to part (a) were mainly the result of failing to draw a diagram. Follow through benefitted many candidates. A high proportion of candidates lost the mark in (e) by not writing their answer as an equation in the form r = …
This was a multi-part question that was well answered by many candidates. Wrong answers to part (a) were mainly the result of failing to draw a diagram. Follow through benefitted many candidates. A high proportion of candidates lost the mark in (e) by not writing their answer as an equation in the form \(\boldsymbol{r} = \) …
This was a multi-part question that was well answered by many candidates. Wrong answers to part (a) were mainly the result of failing to draw a diagram. Follow through benefitted many candidates. A high proportion of candidates lost the mark in (e) by not writing their answer as an equation in the form r = …
This was a multi-part question that was well answered by many candidates. Wrong answers to part (a) were mainly the result of failing to draw a diagram. Follow through benefitted many candidates. A high proportion of candidates lost the mark in (e) by not writing their answer as an equation in the form r = …
Question
Consider the planes \({\pi _1}:x – 2y – 3z = 2{\text{ and }}{\pi _2}:2x – y – z = k\) .
Find the angle between the planes \({\pi _1}\)and \({\pi _2}\) .[4]
The planes \({\pi _1}\) and \({\pi _2}\) intersect in the line \({L_1}\) . Show that the vector equation of
\({L_1}\) is \(r = \left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\)[5]
The line \({L_2}\) has Cartesian equation \(5 – x = y + 3 = 2 – 2z\) . The lines \({L_1}\) and \({L_2}\) intersect at a point X. Find the coordinates of X.[5]
Determine a Cartesian equation of the plane \({\pi _3}\) containing both lines \({L_1}\) and \({L_2}\) .[5]
Let Y be a point on \({L_1}\) and Z be a point on \({L_2}\) such that XY is perpendicular to YZ and the area of the triangle XYZ is 3. Find the perimeter of the triangle XYZ.[5]
▶️Answer/Explanation
Markscheme
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
\(\boldsymbol{n} = \left( {\begin{array}{*{20}{c}}
1 \\
{ – 2} \\
{ – 3}
\end{array}} \right)\) and \(\boldsymbol{m} = \left( {\begin{array}{*{20}{c}}
2 \\
{ – 1} \\
{ – 1}
\end{array}} \right)\) (A1)
\(\cos \theta = \frac{{\boldsymbol{n} \cdot \boldsymbol{m}}}{{\left| \boldsymbol{n} \right|\left| \boldsymbol{m} \right|}}\) (M1)
\(\cos \theta = \frac{{2 + 2 + 3}}{{\sqrt {1 + 4 + 9} \sqrt {4 + 1 + 1} }} = \frac{7}{{\sqrt {14} \sqrt 6 }}\) A1
\(\theta = 40.2^\circ \,\,\,\,\,(0.702{\text{ rad}})\) A1
[4 marks]
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
METHOD 1
eliminate z from x – 2y – 3z = 2 and 2x – y – z = k
\(5x – y = 3k – 2 \Rightarrow x = \frac{{y – (2 – 3k)}}{5}\) M1A1
eliminate y from x – 2y – 3z = 2 and 2x – y – z = k
\(3x + z = 2k – 2 \Rightarrow x = \frac{{z – (2k – 2)}}{{ – 3}}\) A1
x = t, y = (2 − 3k) + 5t and z = (2k − 2) − 3t A1A1
\(r = \left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) AG
[5 marks]
METHOD 2
\(\left( {\begin{array}{*{20}{c}}
1\\
{ – 2}\\
{ – 3}
\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}
2\\
{ – 1}\\
{ – 1}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
{ – 5}\\
3
\end{array}} \right) \Rightarrow {\text{direction is }}\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) M1A1
Let x = 0
\(0 – 2y – 3z = 2{\text{ and }}2 \times 0 – y – z = k\) (M1)
solve simultaneously (M1)
\(y = 2 – 3k{\text{ and }}z = 2k – 2\) A1
therefore r \( = \left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) AG
[5 marks]
METHOD 3
substitute \(x = t,{\text{ }}y = (2 – 3k) + 5t{\text{ and }}z = (2k – 2) – 3t{\text{ into }}{\pi _1}{\text{ and }}{\pi _2}\) M1
for \({\pi _1}:t – 2(2 – 3k + 5t) – 3(2k – 2 – 3t) = 2\) A1
for \({\pi _2}:2t – (2 – 3k + 5t) – (2k – 2 – 3t) = k\) A1
the planes have a unique line of intersection R2
therefore the line is \(r = \left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) AG
[5 marks]
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
\(5 – t = (2 – 3k + 5t) + 3 = 2 – 2(2k – 2 – 3t)\) M1A1
Note: Award M1A1 if candidates use vector or parametric equations of \({L_2}\)
eg \(\left( {\begin{array}{*{20}{c}}
0\\
{2 – 3k}\\
{2k – 2}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
5\\
{ – 3}\\
1
\end{array}} \right) + s\left( {\begin{array}{*{20}{c}}
{ – 2}\\
2\\
{ – 1}
\end{array}} \right)\) or \( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 5 – 2s}\\
{2 – 3k + 5t = – 3 + 2s}\\
{2k – 2 – 3t = 1 + s}
\end{array}} \right.\)
solve simultaneously M1
\(k = 2,{\text{ }}t = 1{\text{ }}(s = 2)\) A1
intersection point (\(1\), \(1\), \( – 1\)) A1
[5 marks]
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
\({\overrightarrow l _2} = \left( {\begin{array}{*{20}{c}}
2\\
{ – 2}\\
1
\end{array}} \right)\) A1
\({\overrightarrow l _1} \times {\overrightarrow l _2} = \left| {\begin{array}{*{20}{c}}
\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k}\\
1&5&{ – 3}\\
2&{ – 2}&1
\end{array}} \right| = \left( {\begin{array}{*{20}{c}}
{ – 1}\\
{ – 7}\\
{ – 12}
\end{array}} \right)\) (M1)A1
\(\boldsymbol{r} \cdot \left( {\begin{array}{*{20}{c}}
1\\
7\\
{12}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1\\
1\\
{ – 1}
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
1\\
7\\
{12}
\end{array}} \right)\) (M1)
\(x + 7y + 12z = – 4\) A1
[5 marks]
Note: Accept alternative notation for vectors (eg \(\langle a{\text{, }}b{\text{, }}c\rangle {\text{ or }}\left( {a{\text{, }}b{\text{, }}c} \right)\)).
Let \(\theta \) be the angle between the lines \({\overrightarrow l _1} = \left( {\begin{array}{*{20}{c}}
1\\
5\\
{ – 3}
\end{array}} \right)\) and \({\overrightarrow l _2} = \left( {\begin{array}{*{20}{c}}
2\\
{ – 2}\\
1
\end{array}} \right)\)
\(\cos \theta = \frac{{\left| {2 – 10 – 3} \right|}}{{\sqrt {35} \sqrt 9 }} \Rightarrow \theta = 0.902334…{\text{ }}51.699…^\circ )\) (M1)
as the triangle XYZ has a right angle at Y,
\({\text{XZ}} = a \Rightarrow {\text{YZ}} = a\sin \theta {\text{ and XY}} = a\cos \theta \) (M1)
\({\text{area = 3}} \Rightarrow \frac{{{a^2}\sin \theta \cos \theta }}{2} = 3\) (M1)
\(a = 3.5122…\) (A1)
perimeter \( = a + a\sin \theta + a\cos \theta = 8.44537… = 8.45\) A1
Note: If candidates attempt to find coordinates of Y and Z award M1 for expression of vector YZ in terms of two parameters, M1 for attempt to use perpendicular condition to determine relation between parameters, M1 for attempt to use the area to find the parameters and A2 for final answer.
[5 marks]
Examiners report
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Although this was the last question in part B, it was answered surprisingly well by many candidates, except for part (e). Even those who had not done so well elsewhere often gained a number of marks in some parts of the question. Nevertheless the presence of parameters seemed to have blocked the abilities of weaker candidates to solve situations in which vectors were involved. Mathematical skills for this particular question were sometimes remarkable, however, calculations proved incomplete due to the way that planes were presented. Most candidates found a correct angle in part (a). Occasional arithmetic errors in calculating the magnitude of a vector and dot product occurred. In part (b) the vector product approach was popular. In some case candidates simply verified the result by substitution. There was a lot of simultaneous equation solving, much of which was not very pretty. In part (c), a number of candidates made errors when attempting to solve a system of equations involving parameters. Many of the results for the point were found in terms of k. It was notorious that candidates did not use their GDC to try to find the coordinates of the intersection point between lines. In part (d), a number of candidates used an incorrect point but this part was often done well.
Very few excellent answers to part (e) were seen using an efficient method. Most candidates attempted methods involving heavy algebraic manipulation and had little success in this part of the question.
Question
The points A and B have position vectors \(\overrightarrow {{\text{OA}}} = \left\{ {\begin{array}{*{20}{c}} 1 \\ 2 \\ { – 2} \end{array}} \right\}\) and \(\overrightarrow {{\text{OB}}} = \left\{ {\begin{array}{*{20}{c}} 1 \\ 0 \\ 2 \end{array}} \right\}\).
a.Find \(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OB}}} \).[2]
b.Hence find the area of the triangle OAB.[2]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OB}}} = \left( {\begin{array}{*{20}{c}} 4 \\ { – 4} \\ { – 2} \end{array}} \right)\) (M1)A1
Note: M1A0 can be awarded for attempt at a correct method shown, or correct method implied by the digits 4, 4, 2 found in the correct order.
[2 marks]
\({\text{area}} = \frac{1}{2}\sqrt {{4^2} + {4^2} + {2^2}} = 3\) M1A1
[2 marks]
Examiners report
Generally well done. Most students were able to obtain full marks on this question. Most of the errors made were due to careless mistakes.
Generally well done. Most students were able to obtain full marks on this question. Most of the errors made were due to careless mistakes. A few students did not take notice of the “hence” in part (b) and were consequently not able to obtain the marks.
