Question
[Maximum mark: 5]
There are 8 numbers in a data set. The sum of the numbers is 48 .
(a) Find the mean. [2]
The variance of this data set is 2 . Each number in the set is multiplied by 3 .
(b) Find the value of:
(i) the new mean;
(ii) the new variance. [3]
Answer/Explanation
(a) We have
$
\begin{aligned}
\text { mean } & =\frac{48}{8} \\
& =6
\end{aligned}
$
(b) (i) We have
$
\begin{aligned}
\text { new mean } & =3 \times(\text { old mean }) \\
& =3 \times 6 \\
& =18
\end{aligned}
$
(ii) We have
$
\begin{aligned}
\text { new variance } & =3^2 \times(\text { old variance }) \\
& =3^2 \times 2 \\
& =18
\end{aligned}
$
Question
[Maximum mark: 6]
A random variable $X$ is normally distributed with $\mu=120$ and $\sigma=15$.
Find the interquartile range of $X$.
Answer/Explanation
If we draw the normal curve for $X$, we have
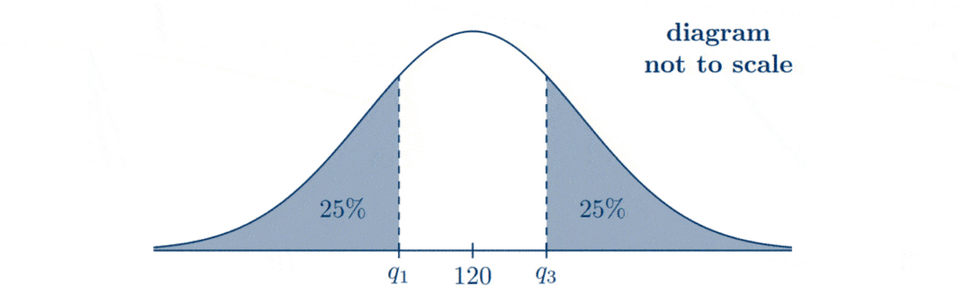
Hence, using $X \sim \mathrm{N}\left(120,15^2\right)$, we get
$
\begin{aligned}
& q_1=\operatorname{invNorm}(0.25,120,15) \approx 109.9 \\
& q_3=\operatorname{invNorm}(0.75,120,15) \approx 130.1
\end{aligned}
$
Hence we obtain
$
\begin{aligned}
\mathrm{IQR} & =q_3-q_1 \\
& =130.1-109.9 \\
& =20.2
\end{aligned}
$
