Question
A bag contains 7 blue and 5 red marbles. Two marbles are selected at random without replacement.
(a) Complete the tree diagram below.
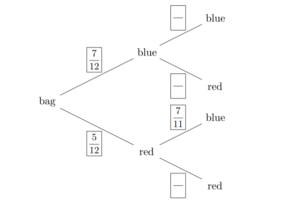
(b) Find the probability that exactly one of the selected marbles is blue.
Answer/Explanation
Ans:
(a) If we complete the tree diagram below, we have
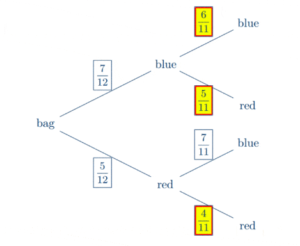
(b) Hence, using the tree diagram from part (a), we get
P(exactly one is blue) = P(blue & red) + P(red & blue)
= P(blue) P(red | blue) + P(red) P(blue | red)
\(=\frac{7}{12}\times \frac{5}{11}\times \frac{5}{12}\times \frac{7}{11}\)
\(=\frac{70}{132}\)
\(=\frac{35}{66}\)
Question
Let f(x) = e3x. The line L is the tangent to the curve of f at (0, 1).
Find the equation of L in the form y = mx + c.
Answer/Explanation
Ans:
First we find m. We have
f ‘(x) = 3e3x
m = f ‘(0)
= 3e0x
= 3
The equation of L is
y – y1 = m(x – x1)
y – 1 = 3(x – 0)
y = 3x + 1
