Question
[Maximum mark: 6]
The diagram below shows quadrilateral $\mathrm{ABCD}$ with side lengths of $\mathrm{AD}=12 \mathrm{~m}, \mathrm{DC}=7 \mathrm{~m}$ and $\mathrm{BC}=5 \mathrm{~m}$. Angle $\mathrm{B\hat{A}} \mathrm{D}=50^{\circ}$ and angle $\mathrm{B\hat{C}}\mathrm{D}=100^{\circ}$.
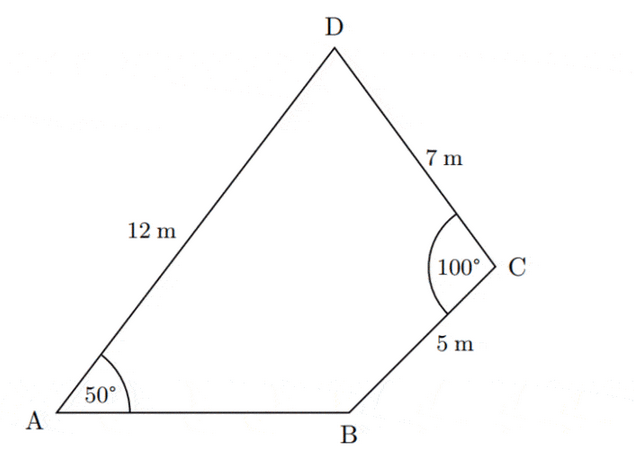
A new line is drawn from B to D direct.
(a) Calculate the length of this new line, $\text{BD}$. [3]
(b) Calculate the size of angle $\mathrm{B\hat{A}} \mathrm{D}$. [3]
Answer/Explanation
(a) Using the cosine rule, we get
$
\begin{aligned}
\mathrm{BD}^2 & =\mathrm{CD}^2+\mathrm{BC}^2-2(\mathrm{CD})(\mathrm{BC}) \cos (\mathrm{B\hat{C}} \mathrm{D}) \\
\mathrm{BD}^2 & =7^2+5^2-2(7)(5) \cos \left(100^{\circ}\right) \\
\mathrm{BD} & =\sqrt{7^2+5^2-2(7)(5) \cos \left(100^{\circ}\right)} \\
& \approx 9.28 \mathrm{~m}
\end{aligned}
$
(b) Using the sine rule, we get
$
\begin{aligned}
\frac{\mathrm{AD}}{\sin (\mathrm{A\hat{B}} \mathrm{D})} & =\frac{\mathrm{BD}}{\sin (\mathrm{B\hat{A}} \mathrm{D})} \\
\frac{12}{\sin (\mathrm{A\hat{B}} \mathrm{D})} & =\frac{9.28}{\sin \left(50^{\circ}\right)} \\
\sin (\mathrm{A\hat{B}} \mathrm{D}) & =\frac{12 \sin \left(50^{\circ}\right)}{9.28} \\
& \approx 0.9906 \\
\mathrm{A\hat{B}} \mathrm{D} & \approx \sin ^{-1}(0.9906) \\
& \approx 82.1^{\circ}
\end{aligned}
$
Question
[Maximum mark: 6]
Atmospheric pressure, $P$, in $\mathrm{kPa}$, decreases exponentially with increasing height above sea level, $h$. The atmospheric pressure can be modelled by the function
$$
P(h)=101 \times\left(\frac{25}{22}\right)^{-h},
$$
where $h$ is the height above sea level in kilometres.
(a) Write down the exact atmospheric pressure at sea level, in $\mathrm{kPa}$. [1]
Mount Kosciuszko is the highest mountain in Australia with a height of 2228 metres above sea level at the top.
(b) Calculate the atmospheric pressure at the top of the Mount Kosciuszko. [2]
(c) Calculate the height where the atmospheric pressure is equal to $10 \mathrm{kPa}$. [3]
Answer/Explanation
(a) $\text{101} \mathrm{kPa}$
(b) Evaluating $P(h)$ for $h=2.228$, we get
$
\begin{aligned}
P(2.228) & =101 \times\left(\frac{25}{22}\right)^{-2.228} \\
& \approx 76.0 \mathrm{kPa}
\end{aligned}
$
(c) Solving the equation $P(h)=10$ for $h$, we obtain
$
\begin{aligned}
101 \times\left(\frac{25}{22}\right)^{-h} & =10 \\
h & =18.1 \mathrm{~km}\quad\text{[by using G.D.C.]}
\end{aligned}
$
