Question
[Maximum mark: 14]
The weights of the edges of a graph $\boldsymbol{H}$ are given in the following table.
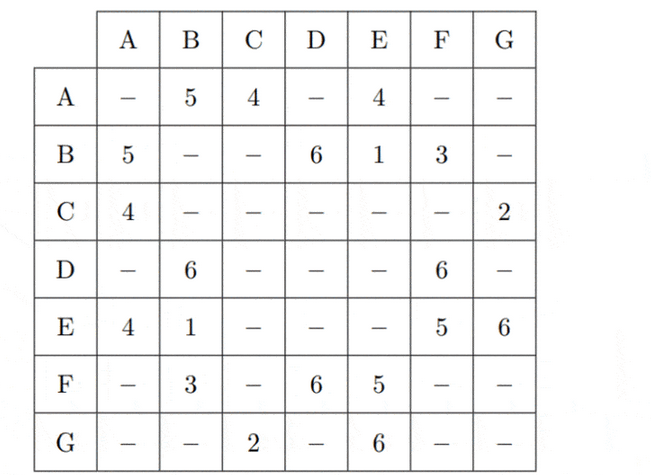
(a) (i) Draw the weighted graph $\boldsymbol{H}$ on the vertices below.

(ii) Using Kruskal’s algorithm, find a minimum spanning tree for $\boldsymbol{H}$. Clearly indicate the order in which the edges are added to the tree.
(iii) Write down the weight of the minimum spanning tree. [8]
Consider the following weighted graph $\boldsymbol{J}$.
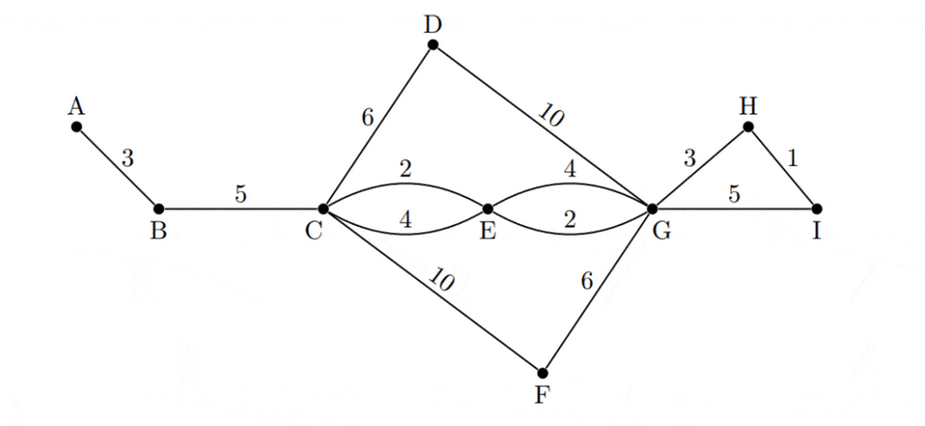
(b) (i) Find a solution to the Chinese postman problem for the graph $\boldsymbol{J}$.
(ii) Write down the total weight of the solution. [3]
(c) (i) State the travelling salesman problem.
(ii) Explain why there is no solution to the travelling salesman problem for the graph $\boldsymbol{J}$. [3]
Answer/Explanation
Ans:
Question
[Maximum mark: 11]
A hot apple pie was taken out of the oven and left cooling on the bench. The temperature of the kitchen is $19^{\circ} \mathrm{C}$. This situation can be modelled by the exponential function $T=a+b\left(k^{-t}\right)$, where $T$ is the temperature of the apple pie, in ${ }^{\circ} \mathrm{C}$, and $t$ is the number of minutes for which the apple pie has been on the bench in the kitchen. A sketch of the situation is given below.
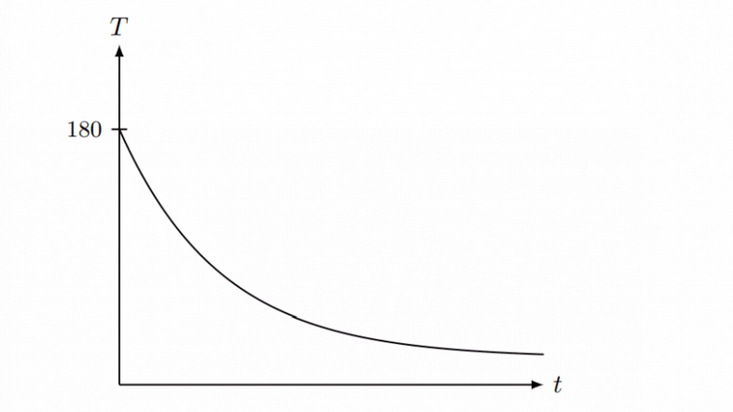
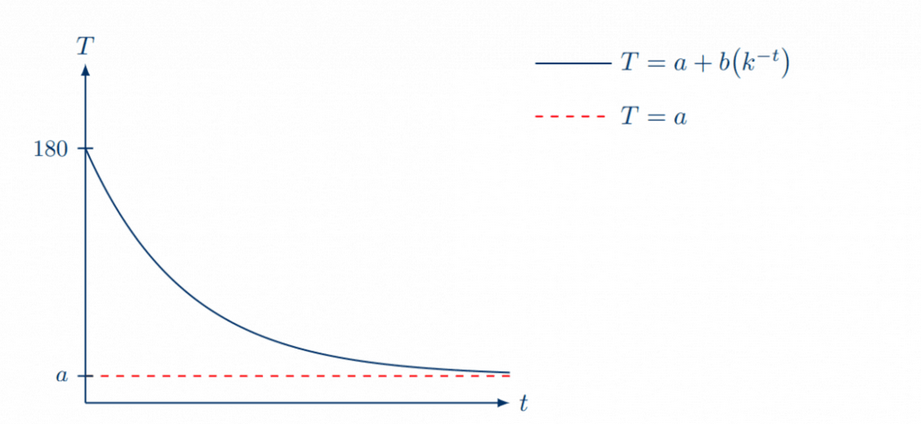
(a) Explain why $a=19$. [2]
Initially, at $t=0$, the temperature of the apple pie is $180^{\circ} \mathrm{C}$.
(b) Find the value of $b$. [2]
After being left cooling on the bench for one minute, the temperature of the apple pie is $159^{\circ} \mathrm{C}$.
(c) Show that $k=1.15$. [2]
(d) Find the temperature of the apple pie five minutes after it has been left cooling on the bench. [2]
(e) Find the total time needed for the apple pie to reach a temperature of $30^{\circ} \mathrm{C}$. Give your answer in minutes and seconds, correct to the nearest second. [3]
Answer/Explanation
(a) We have
$
\begin{aligned}
T & =a+b\left(k^{-t}\right) \\
T & =a
\end{aligned}
$
On the other hand, we know the temperature of the apple pie cannot fall below the temperature of the kitchen.
Hence we must have $a=19$.
(b) When $t=0$, we have $T=180$.
Hence we get
$
\begin{aligned}
19+b\left(k^0\right) & =180 \\
19+b & =180 \\
b & =161\quad\text{[by using G.D.C.]}
\end{aligned}
$
