Question
[Maximum mark: 5]
There are two traffic lights on a road below a $120 \mathrm{~m}$ high skyscraper. From the top of the skyscraper, the traffic lights can be seen at angles of depression of $35^{\circ}$ and $65^{\circ}$ on each side of the skyscraper, as illustrated in the diagram below.
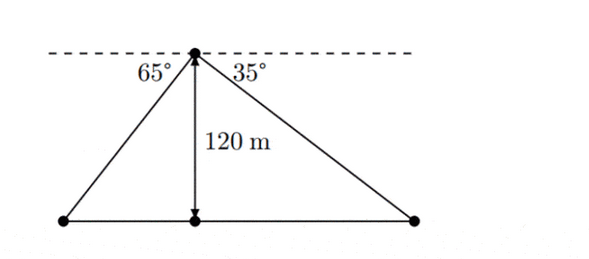
Find the distance between the two traffic lights, correct to the nearest whole metre.
Answer/Explanation
Consider the following triangles:
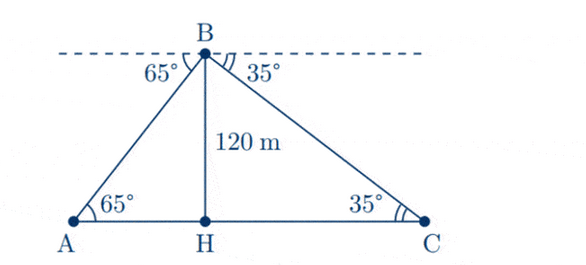
From the right-angled triangle $\mathrm{ABH}$, we get
$
\begin{aligned}
\tan (\mathrm{B\hat{A}} \text {H}) & =\frac{\mathrm{BH}}{\mathrm{AH}} \\
\tan \left(65^{\circ}\right) & =\frac{120}{\mathrm{AH}} \\
\mathrm{AH} & =\frac{120}{\tan \left(65^{\circ}\right)} \\
& \approx 56.0 \mathrm{~m}
\end{aligned}
$
From the right-angled triangle HBC, we get
$
\begin{aligned}
\tan (\mathrm{B\hat{C}} \text{H}) & =\frac{\mathrm{BH}}{\mathrm{CH}} \\
\tan \left(35^{\circ}\right) & =\frac{120}{\mathrm{CH}} \\
\mathrm{CH} & =\frac{120}{\tan \left(35^{\circ}\right)} \\
& \approx 171 \mathrm{~m} .
\end{aligned}
$
Hence
$
\begin{aligned}
\mathrm{AC} & =\mathrm{AH}+\mathrm{CH} \\
& =56+171 \\
& \approx 227 \mathrm{~m}
\end{aligned}
$$
Question
[Maximum mark: 6]
At the beginning of each year, Jack invests $\$ 5000$ in a savings account that pays $4 \%$ annual interest, compounded quarterly
(a) Find the number of years it will take until Jack has $\$ 100000$ in his account. [3]
At the beginning of each year, John invests $\$ 6000$ in a savings account that pays an annual interest rate, compounded semi-annually. After 20 years John has $\$ 200000$ in his account.
(b) Find the annual interest rate. [3]
Answer/Explanation
(a) Using the TVM Solver on G.D.C., we have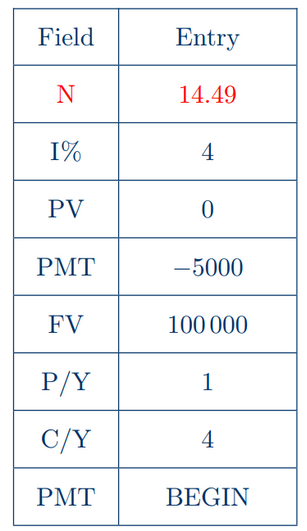
$\text{Hence it will take 14.5 years until Jack has \$ 100000 in his account.}$
(b) Using the TVM Solver on G.D.C., we have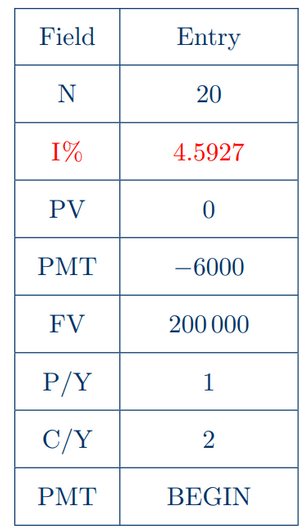
$\text{Hence the annual interest rate is}$ $4.59 \%$
