Question
[Maximum mark: 6]
After solving a problem, John has an exact answer of $z=0.1475$.
(a) Write down the exact value of $z$ in the form $a \times 10^k$, where $1 \leq a<10, k \in \mathbb{Z}$. [2]
(b) State the value of $z$ given correct to 2 significant figures. [1]
(c) Calculate the percentage error if $z$ is given correct to 2 significant figures. [3]
Answer/Explanation
(a) $1.475 \times 10^{-1}$
(b) $0.15$
(c) Using the percentage error formula $\epsilon=\left|\frac{v_{\mathrm{A}}-v_{\mathrm{E}}}{v_{\mathrm{E}}}\right| \times 100 \%$ with $v_{\mathrm{E}}=0.1475$ and $v_{\mathrm{A}}=0.15$, we obtain
$
\begin{aligned}
\epsilon & =\left|\frac{0.15-0.1475}{0.1475}\right| \times 100 \% \\
& \approx 1.69 \%
\end{aligned}
$
Question
[Maximum mark: 6]
The number of days rain per month in London varies depending on the time of year. The data shows the number of wet days per month.
$$
\begin{array}{llllllllllll}
17 & 13 & 11 & 14 & 13 & 11 & 13 & 12 & 13 & 14 & 16 & 16
\end{array}
$$
(a) For this data, find
(i) the median;
(ii) the minimum and maximum values. [3]
The lower quartile of the data is $12.5$ and the upper quartile of the data is 15 .
(b) Draw a box-and-whisker diagram to represent the data. [3]
Answer/Explanation
(a) (i) First, rearrange the data in ascending order:
$\begin{array}{llllllllllll}11 & 11 & 12 & 13 & 13 & 13 & 13 & 14 & 14 & 16 & 16 & 17\end{array}$
The median of a data set is the number in the middle. Since there are 12 numbers in total, the median is the average of the 6 th and 7 th numbers, which are 13 and 13. Hence,
$
\begin{aligned}
{[\text { median }] } & =\frac{13+13}{2} \\
& =13
\end{aligned}
$
(ii) $\operatorname{Min}=11, \operatorname{Max}=17$
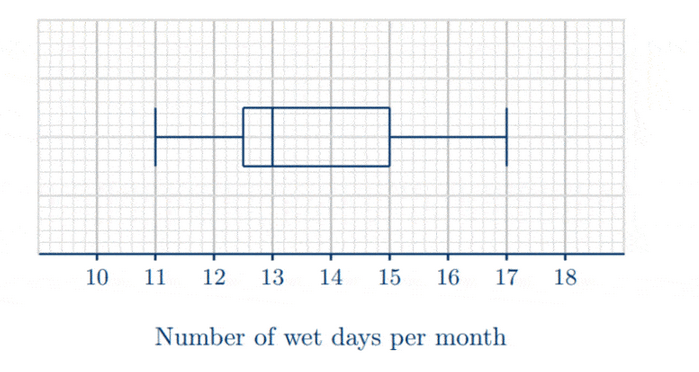
(b) We have the five-number summary of the given data set as follows.
- $\operatorname{Min}=11$
- $Q_1=12.5$
- Median $=13$
- $Q_3=15$
- $\operatorname{Max}=17$
Based off the summary above, we can draw the box-and-whisker diagram as following.