[Maximum mark: 19]
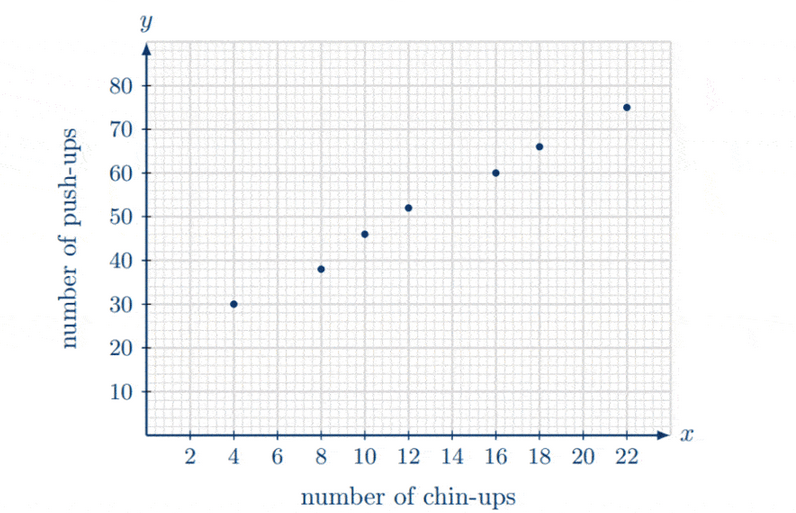
The following table shows the number of chin-ups and the number of push-ups performed by seven college athletes.

(a) Draw a scatter diagram for the above data on the axes below. Use a scale of 1 unit to represent 2 chin-ups on the $x$-axis and 1 unit to represent 10 push-ups on the $y$-axis. [3]
(b) (i) Find the Pearson’s product-moment correlation coefficient, $r$, for the above data.
(ii) Describe the correlation between the number of chin-ups and the number of push-ups. [4]
(c) Find the
(i) mean number of chin-ups, $\bar{x}$;
(ii) mean number of push-ups, $\bar{y}$. [2]
(d) Plot and label the point $\mathrm{M}(\bar{x}, \bar{y})$ on your scatter diagram from part (a). [2]
(e) Find the line of regression equation $y$ on $x$. [2]
(f) Use your equation from part (e) to estimate the number of push-ups of a college athlete who performed 14 chin-ups.
(g) Draw the regression line $y$ on $x$ on your scatter diagram from part (a). [2]
A new college athlete performs 30 chin-ups and uses the above data to estimate that he will perform 96 push-ups.
(h) State whether this estimate is reliable and give a reason for your answer. [2]
Answer/Explanation
(a) The scatter plot is as follows.
Question
[Maximum mark: 15]
A triangular farm is shown in the diagram below. A river runs along the edge from $\mathrm{A}$ to $\mathrm{B}$ and the farm house is located at $\mathrm{C}$, a safe distance from the river. The distance from the farm house to point A is $270 \mathrm{~m}$ and to point B is $360 \mathrm{~m}$. The angle $\mathrm{A\hat{C}}\mathrm{B}$ is $130^{\circ}$.
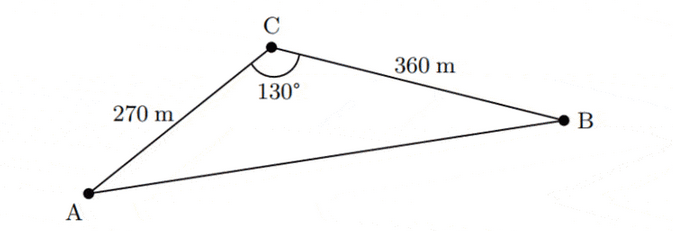
(a) Calculate the distance along the river from A to B. [2]
The cost of fencing is 130 Australian dollars (AUD) per metre.
(b) Calculate the total cost of fencing the whole perimeter of the farm, providing your answer to the nearest dollar. [2]
(c) Find the sizes of angels $\mathrm{C\hat{A}}\mathrm{B}$ and $\mathrm{A\hat{B}}\mathrm{C}$.
(d) Calculate the area of the farm. Give your answer correct to the nearest whole square metre. [2]
(e) Calculate the shortest distance from the farm house to the river. [3]
A tower is located at point B. The angle of elevation to the top of the tower, H, from point $\mathrm{C}$ is measured to be $1^{\circ}$.
(f) Calculate the vertical height, $\mathrm{BH}$, of the tower, correct to the nearest centimetre. [2]
(g) Calculate the distance between the top of the tower, $\mathrm{H}$, to point A. [2]
Answer/Explanation
(a) Using the cosine rule, we get
$
\begin{aligned}
\mathrm{AB}^2 & =\mathrm{AC}^2+\mathrm{BC}^2-2(\mathrm{AC})(\mathrm{BC}) \cos (\mathrm{A\hat{C}}\mathrm{B}) \\
\mathrm{AB}^2 & =270^2+360^2-2(270)(360) \cos \left(130^{\circ}\right) \\
& \approx 327457.91 \\
\mathrm{AB} & \approx \sqrt{327457.91} \\
& \approx 572 \mathrm{~m}
\end{aligned}
$
(b) First, let’s find the perimeter of the farm
$
\begin{aligned}
p & =\mathrm{AB}+\mathrm{BC}+\mathrm{AC} \\
& =572+360+270 \\
& =1202 \mathrm{~m}
\end{aligned}
$
The total cost of fencing can be found by multiplying the number of metres by the cost per metre:
$
\begin{aligned}
\text { Cost } & =(1202)(130) \\
& =\$ 156260
\end{aligned}
$
