Question
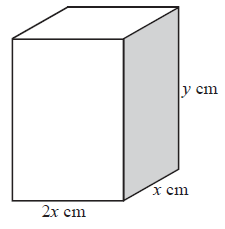
A closed rectangular box has a height \(y{\text{ cm}}\) and width \(x{\text{ cm}}\). Its length is twice its width. It has a fixed outer surface area of \(300{\text{ c}}{{\text{m}}^2}\) .
Factorise \(3{x^2} + 13x – 10\).[2]
Solve the equation \(3{x^2} + 13x – 10 = 0\).[2]
Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Find the equation of the axis of symmetry on the graph of this function.[2]
Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Calculate the minimum value of this function.[2]
Show that \(4{x^2} + 6xy = 300\).[2]
Find an expression for \(y\) in terms of \(x\).[2]
Hence show that the volume \(V\) of the box is given by \(V = 100x – \frac{4}{3}{x^3}\).[2]
Find \(\frac{{{\text{d}}V}}{{{\text{d}}x}}\).[2]
(i) Hence find the value of \(x\) and of \(y\) required to make the volume of the box a maximum.
(ii) Calculate the maximum volume.[5]
Answer/Explanation
Markscheme
\((3x – 2)(x + 5)\) (A1)(A1)[2 marks]
\((3x – 2)(x + 5) = 0\)
\(x = \frac{2}{3}\) or \(x = – 5\) (A1)(ft)(A1)(ft)(G2)[2 marks]
\(x = \frac{{ – 13}}{6}{\text{ }}( – 2.17)\) (A1)(A1)(ft)(G2)
Note: (A1) is for \(x = \), (A1) for value. (ft) if value is half way between roots in (b).[2 marks]
Minimum \(y = 3{\left( {\frac{{ – 13}}{6}} \right)^2} + 13\left( {\frac{{ – 13}}{6}} \right) – 10\) (M1)
Note: (M1) for substituting their value of \(x\) from (c) into \(f(x)\) .
\( = – 24.1\) (A1)(ft)(G2)[2 marks]
\({\text{Area}} = 2(2x)x + 2xy + 2(2x)y\) (M1)(A1)
Note: (M1) for using the correct surface area formula (which can be implied if numbers in the correct place). (A1) for using correct numbers.
\(300 = 4{x^2} + 6xy\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(6xy = 300 – 4{x^2}\) (M1)
\(y = \frac{{300 – 4{x^2}}}{{6x}}\) or \(\frac{{150 – 2{x^2}}}{{3x}}\) (A1)[2 marks]
\({\text{Volume}} = x(2x)y\) (M1)
\(V = 2{x^2}\left( {\frac{{300 – 4{x^2}}}{{6x}}} \right)\) (A1)(ft)
\( = 100x – \frac{4}{3}{x^3}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 100 – \frac{{12{x^2}}}{3}\) or \(100 – 4{x^2}\) (A1)(A1)
Note: (A1) for each term.[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column
(i) For maximum \(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) or \(100 – 4{x^2} = 0\) (M1)
\(x = 5\) (A1)(ft)
\(y = \frac{{300 – 4{{(5)}^2}}}{{6(5)}}\) or \(\left( {\frac{{150 – 2{{(5)}^2}}}{{3(5)}}} \right)\) (M1)
\( = \frac{{20}}{3}\) (A1)(ft)
(UP) (ii) \(333\frac{1}{3}{\text{ c}}{{\text{m}}^3}{\text{ }}(333{\text{ c}}{{\text{m}}^3})\)
Note: (ft) from their (e)(i) if working for volume is seen.[5 marks]
Question
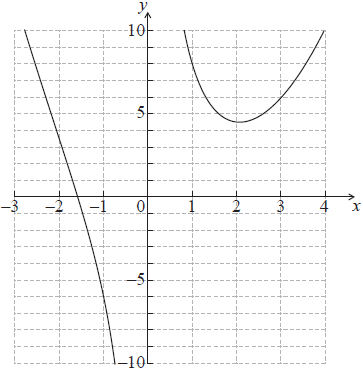
The diagram shows part of the graph of \(f(x) = {x^2} – 2x + \frac{9}{x}\) , where \(x \ne 0\) .
Write down
(i) the equation of the vertical asymptote to the graph of \(y = f (x)\) ;
(ii) the solution to the equation \(f (x) = 0\) ;
(iii) the coordinates of the local minimum point.[5]
Find \(f'(x)\) .[4]
Show that \(f'(x)\) can be written as \(f'(x) = \frac{{2{x^3} – 2{x^2} – 9}}{{{x^2}}}\) .[2]
Find the gradient of the tangent to \(y = f (x)\) at the point \({\text{A}}(1{\text{, }}8)\) .[2]
The line, \(L\), passes through the point A and is perpendicular to the tangent at A.
Write down the gradient of \(L\) .[1]
The line, \(L\) , passes through the point A and is perpendicular to the tangent at A.
Find the equation of \(L\) . Give your answer in the form \(y = mx + c\) .[3]
The line, \(L\) , passes through the point A and is perpendicular to the tangent at A.
\(L\) also intersects the graph of \(y = f (x)\) at points B and C . Write down the x-coordinate of B and of C .[2]
Answer/Explanation
Markscheme
(i) \(x = 0\) (A1)(A1)
Note: Award (A1) for \(x = \) a constant, (A1) for the constant in their equation being \(0\).
(ii) \( – 1.58\) (\( – 1.58454 \ldots \)) (G1)
Note: Accept \( – 1.6\), do not accept \( – 2\) or \( – 1.59\).
(iii) \((2.06{\text{, }}4.49)\) \((2.06020 \ldots {\text{, }}4.49253 \ldots )\) (G1)(G1)
Note: Award at most (G1)(G0) if brackets not used. Award (G0)(G1)(ft) if coordinates are reversed.
Note: Accept \(x = 2.06\), \(y = 4.49\) .
Note: Accept \(2.1\), do not accept \(2.0\) or \(2\). Accept \(4.5\), do not accept \(5\) or \(4.50\).[5 marks]
\(f'(x) = 2x – 2 – \frac{9}{{{x^2}}}\) (A1)(A1)(A1)(A1)
Notes: Award (A1) for \(2x\), (A1) for \( – 2\), (A1) for \( – 9\), (A1) for \({x^{ – 2}}\) . Award a maximum of (A1)(A1)(A1)(A0) if there are extra terms present.[4 marks]
\(f'(x) = \frac{{{x^2}(2x – 2)}}{{{x^2}}} – \frac{9}{{{x^2}}}\) (M1)
Note: Award (M1) for taking the correct common denominator.
\( = \frac{{(2{x^3} – 2{x^2})}}{{{x^2}}} – \frac{9}{{{x^2}}}\) (M1)
Note: Award (M1) for multiplying brackets or equivalent.
\( = \frac{{2{x^3} – 2{x^2} – 9}}{{{x^2}}}\) (AG)
Note: The final (M1) is not awarded if the given answer is not seen.[2 marks]
\(f'(1) = \frac{{2{{(1)}^3} – 2(1) – 9}}{{{{(1)}^2}}}\) (M1)
\( = – 9\) (A1)(G2)
Note: Award (M1) for substitution into given (or their correct) \(f'(x)\) . There is no follow through for use of their incorrect derivative.[2 marks]
\(\frac{1}{9}\) (A1)(ft)
Note: Follow through from part (d).[1 mark]
\(y – 8 = \frac{1}{9}(x – 1)\) (M1)(M1)
Notes: Award (M1) for substitution of their gradient from (e), (M1) for substitution of given point. Accept all forms of straight line.
\(y = \frac{1}{9}x + \frac{{71}}{9}\) (\(y = 0.111111 \ldots x + 7.88888 \ldots \)) (A1)(ft)(G3)
Note: Award the final (A1)(ft) for a correctly rearranged formula of their straight line in (f). Accept \(0.11x\), do not accept \(0.1x\). Accept \(7.9\), do not accept \(7.88\), do not accept \(7.8\).[3 marks]
\( – 2.50\), \(3.61\) (\( – 2.49545 \ldots \), \(3.60656 \ldots \)) (A1)(ft)(A1)(ft)
Notes: Follow through from their line \(L\) from part (f) even if no working shown. Award at most (A0)(A1)(ft) if their correct coordinate pairs given.
Note: Accept \( – 2.5\), do not accept \( – 2.49\). Accept \(3.6\), do not accept \(3.60\).[2 marks]
Question
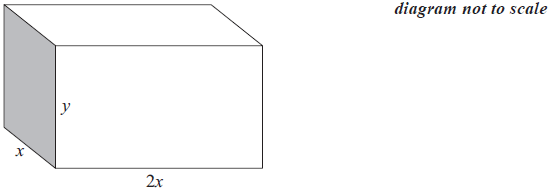
A shipping container is to be made with six rectangular faces, as shown in the diagram.
The dimensions of the container are
length 2x
width x
height y.
All of the measurements are in metres. The total length of all twelve edges is 48 metres.
Show that y =12 − 3x .[3]
Show that the volume V m3 of the container is given by
V = 24x2 − 6x3[2]
Find \( \frac{{\text{d}V}}{{\text{d}x}}\).[2]
Find the value of x for which V is a maximum.[3]
Find the maximum volume of the container.[2]
Find the length and height of the container for which the volume is a maximum.[3]
The shipping container is to be painted. One litre of paint covers an area of 15 m2 . Paint comes in tins containing four litres.
Calculate the number of tins required to paint the shipping container.[4]
Answer/Explanation
Markscheme
\(4(2x) + 4y + 4x = 48\) (M1)
Note: Award (M1) for setting up the equation.
\(12x + 4y = 48\) (M1)
Note: Award (M1) for simplifying (can be implied).
\(y = \frac{{48 – 12x}}{{4}}\) OR \(3x + y =12\) (A1)
\(y =12 – 3x\) (AG)
Note: The last line must be seen for the (A1) to be awarded.[3 marks]
\(V = 2x \times x \times (12 – 3x)\) (M1)(A1)
Note: Award (M1) for substitution into volume equation, (A1) for correct substitution.
\(= 24x^2 – 6x^3\) (AG)
Note: The last line must be seen for the (A1) to be awarded.[2 marks]
\(\frac{{\text{d}V}}{{\text{d}x}} = 48x – 18x^2\) (A1)(A1)
Note: Award (A1) for each correct term.[2 marks]
\(48x -18x^2 = 0\) (M1)(M1)
Note: Award (M1) for using their derivative, (M1) for equating their answer to part (c) to 0.
OR
(M1) for sketch of \(V = 24x^2 – 6x^3\), (M1) for the maximum point indicated (M1)(M1)
OR
(M1) for sketch of \(\frac{{\text{d}V}}{{\text{d}x}} = 48x – 18x^2\), (M1) for the positive root indicated (M1)(M1)
\(2.67\left( {\frac{{24}}{9},{\text{ }}\frac{8}{3},{\text{ }}2.66666…} \right)\) (A1)(ft)(G2)
Note: Follow through from their part (c).[3 marks]
\(V = 24 \times {\left( {\frac{8}{3}} \right)^2} – 6 \times {\left( {\frac{8}{3}} \right)^3}\) (M1)
Note: Award (M1) for substitution of their value from part (d) into volume equation.
\(56.9({{\text{m}}^3})\left( {\frac{{512}}{9},{\text{ }}56.8888…} \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (d).[2 marks]
\(\text{length} = \frac{{16}}{{3}}\) (A1)(ft)(G1)
Note: Follow through from their answer to part (d). Accept 5.34 from use of 2.67
\(\text{height} = 12 – 3 \times \left( {\frac{{8}}{{3}}} \right) = 4\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for substitution of their answer to part (d), (A1)(ft) for answer. Accept 3.99 from use of 2.67.[3 marks]
\(\text{SA} = 2 \times \frac{{16}}{{3}} \times 4 + 2 \times \frac{{8}}{{3}} \times 4 + 2 \times \frac{{16}}{{3}} \times \frac{{8}}{{3}}\) (M1)
OR
\(\text{SA} = 4 \left( {\frac{{8}}{{3}}}\right)^2 + 6 \times \frac{{8}}{{3}} \times 4\) (M1)
Note: Award (M1) for substitution of their values from parts (d) and (f) into formula for surface area.
92.4 (m2) (92.4444…(m2)) (A1)
Note: Accept 92.5 (92.4622…) from use of 3 sf answers.
\(\text{Number of tins} = \frac{{92.4444…}}{{15 \times 4}}( = 1.54)\) (M1)[4 marks]
Note: Award (M1) for division of their surface area by 60.
2 tins required (A1)(ft)
Note: Follow through from their answers to parts (d) and (f).
