Question
Daniel wants to invest \(\$ 25\,000\) for a total of three years. There are two investment options.
Option One pays compound interest at a nominal annual rate of interest of 5 %, compounded annually.
Option Two pays compound interest at a nominal annual rate of interest of 4.8 %, compounded monthly.
An arithmetic sequence is defined as
un = 135 + 7n, n = 1, 2, 3, …
Calculate the value of his investment at the end of the third year for each investment option, correct to two decimal places.[8]
Determine Daniel’s best investment option.[1]
Calculate u1, the first term in the sequence.[2]
Show that the common difference is 7.[2]
Sn is the sum of the first n terms of the sequence.
Find an expression for Sn. Give your answer in the form Sn = An2 + Bn, where A and B are constants.[3]
The first term, v1, of a geometric sequence is 20 and its fourth term v4 is 67.5.
Show that the common ratio, r, of the geometric sequence is 1.5.[2]
Tn is the sum of the first n terms of the geometric sequence.
Calculate T7, the sum of the first seven terms of the geometric sequence.[2]
Tn is the sum of the first n terms of the geometric sequence.
Use your graphic display calculator to find the smallest value of n for which Tn > Sn.[2]
Answer/Explanation
Markscheme
Option 1: Amount \( = 25\,000{\left( {1 + \frac{5}{{100}}} \right)^3}\) (M1)(A1)
= \(28\,940.63\) (A1)(G2)
Note: Award (M1) for substitution in compound interest formula, (A1) for correct substitution. Give full credit for use of lists.
Option 2: Amount \( = 25\,000{\left( {1 + \frac{{4.8}}{{12(100)}}} \right)^{3 \times 12}}\) (M1)
= \(28\,863.81\) (A1)(G2)
Note: Award (M1) for correct substitution in the compound interest formula. Give full credit for use of lists.[8 marks]
Option 1 is the best investment option. (A1)(ft)[1 mark]
u1 = 135 + 7(1) (M1)
= 142 (A1)(G2)[2 marks]
u2 = 135 + 7(2) = 149 (M1)
d = 149 – 142 OR alternatives (M1)(ft)
d = 7 (AG)[2 marks]
\({S_n} = \frac{{n[2(142) + 7(n – 1)]}}{2}\) (M1)(ft)
Note: Award (M1) for correct substitution in correct formula.
\( = \frac{{n[277 + 7n]}}{2}\) OR equivalent (A1)
\( = \frac{{7{n^2}}}{2} + \frac{{277n}}{2}\) (= 3.5n2 + 138.5n) (A1)(G3)[3 marks]
20r3 = 67.5 (M1)
r3 = 3.375 OR \(r = \sqrt[3]{{3.375}}\) (A1)
r = 1.5 (AG)[2 marks]
\({T_7} = \frac{{20({{1.5}^7} – 1)}}{{(1.5 – 1)}}\) (M1)
Note: Award (M1) for correct substitution in correct formula.
= 643 (accept 643.4375) (A1)(G2)[2 marks]
\(\frac{{20({{1.5}^n} – 1)}}{{(1.5 – 1)}} > \frac{{7{n^2}}}{2} + \frac{{277n}}{2}\) (M1)
Note: Award (M1) for an attempt using lists or for relevant graph.
n = 10 (A1)(ft)(G2)
Note: Follow through from their (c).[2 marks]
Question
A gardener has to pave a rectangular area 15.4 metres long and 5.5 metres wide using rectangular bricks. The bricks are 22 cm long and 11 cm wide.
The gardener decides to have a triangular lawn ABC, instead of paving, in the middle of the rectangular area, as shown in the diagram below.
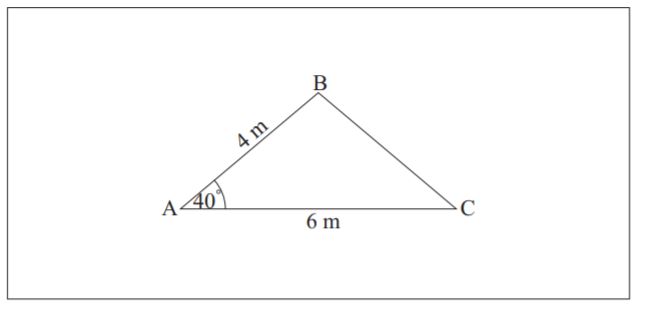
The distance AB is 4 metres, AC is 6 metres and angle BAC is 40°.
In another garden, twelve of the same rectangular bricks are to be used to make an edge around a small garden bed as shown in the diagrams below. FH is the length of a brick and C is the centre of the garden bed. M and N are the midpoints of the long edges of the bricks on opposite sides of the garden bed.
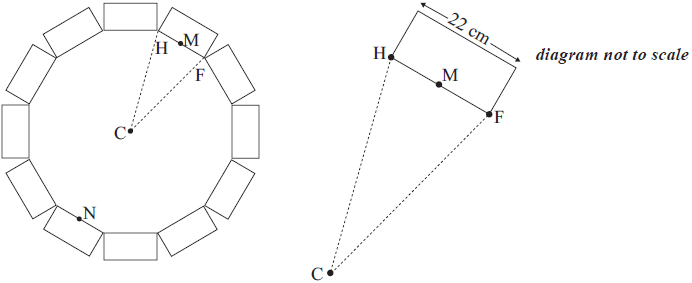
The garden bed has an area of 5419 cm2. It is covered with soil to a depth of 2.5 cm.
It is estimated that 1 kilogram of soil occupies 514 cm3.
Calculate the total area to be paved. Give your answer in cm2.[3]
Write down the area of each brick.[1]
Find how many bricks are required to pave the total area.[2]
Find the length of BC.[3]
Hence write down the perimeter of the triangular lawn.[1]
Calculate the area of the lawn.[2]
Find the percentage of the rectangular area which is to be lawn.[3]
Find the angle FCH.[2]
Calculate the distance MN from one side of the garden bed to the other, passing through C.[3]
Find the volume of soil used.[2]
Find the number of kilograms of soil required for this garden bed.[2]
Answer/Explanation
Markscheme
15.4 × 5.5 (M1)
84.7 m2 (A1)
= 847000 cm2 (A1)(G3)
Note: Award (G2) if 84.7 m2 seen with no working.
OR
1540 × 550 (A1)(M1)
= 847000 cm2 (A1)(ft)(G3)
Note: Award (A1) for both dimensions converted correctly to cm, (M1) for multiplication of both dimensions. (A1)(ft) for correct product of their sides in cm.[3 marks]
242 cm2 (0.0242 m2) (A1)[1 marks}
\(\frac {15.4}{0.22} = 70\) (M1)
\(\frac{5.5}{0.11} = 50\)
\(70 \times 50 = 3500\) (A1)(G2)
OR
\(\frac {847000}{242} = 3500\) (M1)(A1)(ft)(G2)
Note: Follow through from parts (a) (i) and (ii).[2 marks]
\({\text{B}}{{\text{C}}^2} = {4^2} + {6^2}-2 \times 4 \times 6 \times \cos 40^\circ \) (M1)(A1)
\({\text{BC}} = 3.90{\text{ m}}\) (A1)(G2)
Note: Award (M1) for correct substituted formula, (A1) for correct substitutions, (A1) for correct answer.[3 marks]
perimeter = 13.9 m (A1)(ft)(G1)
Notes: Follow through from part (b) (i).[1 mark]
\({\text{Area}} = \frac{1}{2} \times 4 \times 6 \times \sin 40^\circ \) (M1)
= 7.71 m2 (A1)(ft)(G2)
Notes: Award (M1) for correct formula and correct substitution, (A1)(ft) for correct answer.[2 marks]
\(\frac{{7.713}}{{84.7}} \times 100{\text{ }}\% = 9.11{\text{ }}\% \) (A1)(M1)(A1)(ft)(G2)
Notes: Accept 9.10 %.
Award (A1) for both measurements correctly written in the same unit, (M1) for correct method, (A1)(ft) for correct answer.
Follow through from (b) (iii) and from consistent error in conversion of units throughout the question.[3 marks]
\(\frac{{360^\circ }}{{12}}\) (M1)
\( = 30^\circ\) (A1)(G2)[2 marks]
\(\text{MN} = 2 \times \frac{11}{\tan 15} \) (A1)(ft)(M1)
OR
\(\text{MN} = 2 \times 11 \tan 75^\circ \)
\({\text{MN}} = 82.1{\text{ cm}}\) (A1)(ft)(G2)
Notes: Award (A1) for 11 and 2 seen (implied by 22 seen), (M1) for dividing by tan15 (or multiplying by tan 75).
Follow through from their angle in part (c) (i).[3 marks]
volume = 5419 × 2.5 (M1)
= 13500 cm3 (A1)(G2)[2 marks]
\(\frac{{13547.34 \ldots }}{{514}} = 26.4\) (M1)(A1)(ft)(G2)
Note: Award (M1) for dividing their part (d) by 514.
Accept 26.3.[2 marks]
Question
In the diagram below A, B and C represent three villages and the line segments AB, BC and CA represent the roads joining them. The lengths of AC and CB are 10 km and 8 km respectively and the size of the angle between them is 150°.
Find the length of the road AB.[3]
Find the size of the angle CAB.[3]
Village D is halfway between A and B. A new road perpendicular to AB and passing through D is built. Let T be the point where this road cuts AC. This information is shown in the diagram below.
Write down the distance from A to D.[1]
Show that the distance from D to T is 2.06 km correct to three significant figures.[2]
A bus starts and ends its journey at A taking the route AD to DT to TA.
Find the total distance for this journey.[3]
The average speed of the bus while it is moving on the road is 70 km h–1. The bus stops for 5 minutes at each of D and T .
Estimate the time taken by the bus to complete its journey. Give your answer correct to the nearest minute.[4]
Answer/Explanation
Markscheme
AB2 = 102 + 82 – 2 × 10 × 8 × cos150° (M1)(A1)
AB = 17.4 km (A1)(G2)
Note: Award (M1) for substitution into correct formula, (A1) for correct substitution, (A1) for correct answer.[3 marks]
\(\frac{8}{{\sin {\text{C}}\hat {\rm A}{\text{B}}}} = \frac{{17.4}}{{\sin 150^\circ }}\) (M1)(A1)
\({\text{C}}\hat {\rm A}{\text{B}} = 13.3^\circ \) (A1)(ft)(G2)
Notes: Award (M1) for substitution into correct formula, (A1) for correct substitution, (A1) for correct answer. Follow through from their answer to part (a).[3 marks]
AD = 8.70 km (8.7 km) (A1)(ft)
Note: Follow through from their answer to part (a).[1 mark]
DT = tan (13.29…°) × 8.697… = 2.0550… (M1)(A1)
= 2.06 (AG)
Notes: Award (M1) for correct substitution in the correct formula, award (A1) for the unrounded answer seen. If 2.06 not seen award at most (M1)(AO).[2 marks]
\(\sqrt {{{8.70}^2} + {{2.06}^2}} + 8.70 + 2.06\) (A1)(M1)
= 19.7 km (A1)(ft)(G2)
Note: Award (A1) for AT, (M1) for adding the three sides of the triangle ADT, (A1)(ft) for answer. Follow through from their answer to part (c).[3 marks]
\(\frac{{19.7}}{{70}} \times 60 + 10\) (M1)(M1)
= 26.9 (A1)(ft)
Note: Award (M1) for time on road in minutes, (M1) for adding 10, (A1)(ft) for unrounded answer. Follow through from their answer to (e).
= 27 (nearest minute) (A1)(ft)(G3)
Note: Award (A1)(ft) for their unrounded answer given to the nearest minute.[4 marks]
Question
Pauline owns a piece of land ABCD in the shape of a quadrilateral. The length of BC is \(190{\text{ m}}\) , the length of CD is \(120{\text{ m}}\) , the length of AD is \(70{\text{ m}}\) , the size of angle BCD is \({75^ \circ }\) and the size of angle BAD is \({115^ \circ }\) .
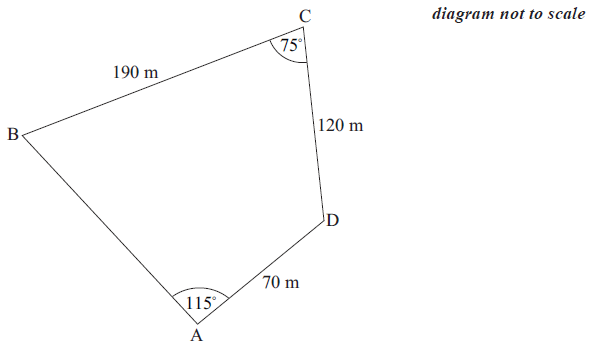
Pauline decides to sell the triangular portion of land ABD . She first builds a straight fence from B to D .
Calculate the length of the fence.[3]
The fence costs \(17\) USD per metre to build.
Calculate the cost of building the fence. Give your answer correct to the nearest USD.[2]
Show that the size of angle ABD is \({18.8^ \circ }\) , correct to three significant figures.[3]
Calculate the area of triangle ABD .[4]
She sells the land for \(120\) USD per square metre.
Calculate the value of the land that Pauline sells. Give your answer correct to the nearest USD.[2]
Pauline invests \(300 000\) USD from the sale of the land in a bank that pays compound interest compounded annually.
Find the interest rate that the bank pays so that the investment will double in value in 15 years.[4]
Answer/Explanation
Markscheme
\({\text{B}}{{\text{D}}^2} = {190^2} + {120^2} – 2(190)(120)\cos {75^ \circ }\) (M1)(A1)
Note: Award (M1) for substituted cosine formula, (A1) for correct substitution.
\(= 197\) m (A1)(G2)
Note: If radians are used award a maximum of (M1)(A1)(A0).[3 marks]
\({\text{cost}} = 196.717 \ldots \times 17\) (M1)
\( = 3344{\text{ USD}}\) (A1)(ft)(G2)
Note: Accept \(3349\) from \(197\).[2 marks]
\(\frac{{\sin ({\text{ABD}})}}{{70}} = \frac{{\sin ({{115}^ \circ })}}{{196.7}}\) (M1)(A1)
Note: Award (M1) for substituted sine formula, (A1) for correct substitution.
\( = {18.81^ \circ } \ldots \) (A1)(ft)
\( = {18.8^ \circ } \) (AG)
Notes: Both the unrounded and rounded answers must be seen for the final (A1) to be awarded. Follow through from their (a). If 197 is used the unrounded answer is \( = {18.78^ \circ } \ldots \)[3 marks]
\({\text{angle BDA}} = {46.2^ \circ }\) (A1)
\({\text{Area}} = \frac{{70 \times (196.717 \ldots ) \times \sin ({{46.2}^ \circ })}}{2}\) (M1)(A1)
Note: Award (M1) for substituted area formula, (A1) for correct substitution.
\({\text{Area ABD}} = 4970{\text{ }}{{\text{m}}^2}\) (A1)(ft)(G2)
Notes: If \(197\) used answer is \(4980\).
Notes: Follow through from (a) only. Award (G2) if there is no working shown and \({46.2^ \circ }\) not seen. If \({46.2^ \circ }\) seen without subsequent working, award (A1)(G2).[4 marks]
\(4969.38 \ldots \times 120\) (M1)
\( = 596 327{\text{ USD}}\) (A1)(ft)(G2)
Notes: Follow through from their (d).[2 marks]
\(300000{\left( {1 + \frac{r}{{100}}} \right)^{15}} = 600000\) or equivalent (A1)(M1)(A1)
Notes: Award (A1) for \(600 000\) seen or implied by alternative formula, (M1) for substituted CI formula, (A1) for correct substitutions.
\(r = 4.73\) (A1)(ft)(G3)
Notes: Award (G3) for \(4.73\) with no working. Award (G2) for \(4.7\) with no working.[4 marks]
Question
Leanne goes fishing at her favourite pond. The pond contains four different types of fish: bream, flathead, whiting and salmon. The fish are either undersized or normal. This information is shown in the table below.
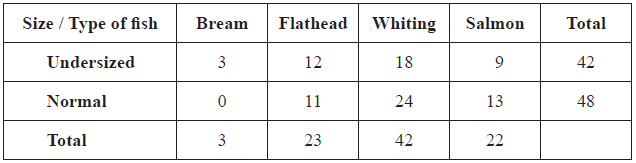
Write down the total number of fish in the pond.[1]
Leanne catches a fish.
Find the probability that she
(i) catches an undersized bream;
(ii) catches either a flathead or an undersized fish or both;
(iii) does not catch an undersized whiting;
(iv) catches a whiting given that the fish was normal.[7]
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Copy and complete the probability tree diagram below.
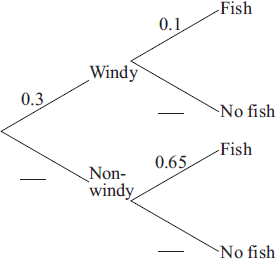[3]
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Calculate the probability that it is windy and Leanne catches a fish on a particular day.[2]
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Calculate the probability that Leanne catches a fish on a particular day.[3]
Use your answer to part (e) to calculate the probability that Leanne catches a fish on two consecutive days.[2]
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Given that Leanne catches a fish on a particular day, calculate the probability that the day was windy.[3]
Answer/Explanation
Markscheme
90 (A1)[1 mark]
(i) \(\frac{3}{{90}}(0.0\bar 3,{\text{ }}0.0333,{\text{ }}0.0333…,{\text{ }}3.\bar 3\% ,{\text{ }}3.33\% )\) (A1)(ft)
Note: For the denominator follow through from their answer in part (a).
(ii) \(\frac{{53}}{{90}}(0.5\bar 8,{\text{ }}0.588…,{\text{ }}0.589,{\text{ }}58.\bar 8\% ,{\text{ }}58.9\% )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for the numerator. (A1)(ft) for denominator. For the denominator follow through from their answer in part (a).
(iii) \(\frac{{72}}{{90}}{\text{(0.8, 80}}\%)\) (A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for the numerator, (their part (a) –18) (A1)(ft) for denominator. For the denominator follow through from their answer in part (a).
(iv) \(\frac{{24}}{{48}}(0.5,{\text{ 50}}\% )\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.[7 marks]
(A1)(A1)(A1)
Notes: Award (A1) for each correct entry. Tree diagram must be seen for marks to be awarded.[3 marks]
\(0.3 \times 0.1 = 0.03\left( {\frac{3}{{100}}} \right)\) (M1)(A1)(G2)
Note: Award (M1) for correct product seen.[2 marks]
\(0.3 \times 0.1+ 0.7\times0.65\) (M1)(M1)
Notes: Award (M1) for \(0.7\times0.65\) (or 0.455) seen, (M1) for adding their 0.03. Follow through from their answers to parts (c) and (d).
\( = 0.485\left( {\frac{{485}}{{1000}},\frac{{97}}{{200}}} \right)\) (A1)(ft)(G2)
Note: Follow through from their tree diagram and their answer to part (d).[3 marks]
\(0.485 \times 0.485\) (M1)
\(0.235\left( {\frac{{9409}}{{40000}}{\text{, }}0.235225} \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (e).[2 marks]
\(\frac{{0.03}}{{0.485}}\) (M1)(A1)(ft)
Notes: Award (M1) for substituted conditional probability formula, (A1)(ft) for their (d) as numerator and their (e) as denominator.
\(0.0619\left( {\frac{{6}}{{97}}}\text{, 0.0618556…} \right) \) (A1)(ft)(G2)
Note: Follow through from their parts (d) and (e).[3 marks]
Question
A contractor is building a house. He first marks out three points A , B and C on the ground such that AB = 5 m , AC = 7 m and angle BAC = 112 °.
Find the length of BC.[3]
He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle BDC is 40° .
Find the size of angle DBC .[4]
He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle BDC is 40° .
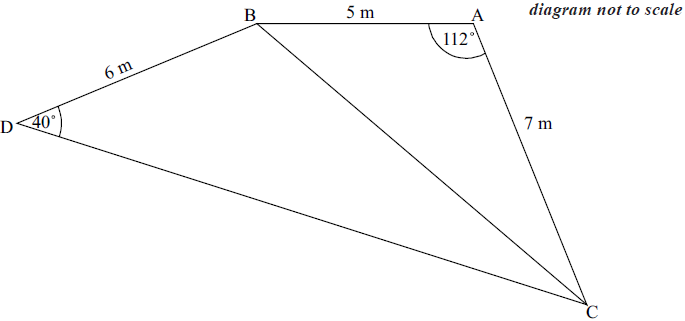
Find the area of the quadrilateral ABDC.[4]
He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle BDC is 40° .
The contractor digs up and removes the soil under the quadrilateral ABDC to a depth of 50 cm for the foundation of the house.
Find the volume of the soil removed. Give your answer in m3 .[3]
He next marks a fourth point, D, on the ground at a distance of 6 m from B , such that angle BDC is 40° .
The contractor digs up and removes the soil under the quadrilateral ABDC to a depth of 50 cm for the foundation of the house.
To transport the soil removed, the contractor uses cylindrical drums with a diameter of 30 cm and a height of 40 cm.
(i) Find the volume of a drum. Give your answer in m3 .
(ii) Find the minimum number of drums required to transport the soil removed.[5]
Answer/Explanation
Markscheme
Units are required in part (c) only.
BC2 = 52 + 72 − 2(5)(7)cos112° (M1)(A1)
Note: Award (M1) for substitution in cosine formula, (A1) for correct substitutions.
BC = 10.0 (m) (10.0111…) (A1)(G2)
Note: If radians are used, award at most (M1)(A1)(A0).[3 marks]
Units are required in part (c) only.
\(\frac{{\sin 40^\circ }}{{10.0111…}} = \frac{{\sin {\text{D}}{\operatorname{\hat C}}{\text{B}}}}{6}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution in sine formula, (A1)(ft) for their correct substitutions. Follow through from their part (a).
\({\text{D}}{\operatorname {\hat C}}{\text{B}}\) = 22.7° (22.6589…) (A1)(ft)
Notes: Award (A2) for 22.7° seen without working. Use of radians results in unrealistic answer. Award a maximum of (M1)(A1)(ft)(A0)(ft). Follow through from their part (a).
\({\text{D}}{\operatorname {\hat C}}{\text{B}}\) = 117° (117.341…) (A1)(ft)(G3)
Notes: Do not penalize if use of radians was already penalized in part (a). Follow through from their answer to part (a).
OR
From use of cosine formula
DC = 13.8(m) (13.8346…) (A1)(ft)
Note: Follow through from their answer to part (a).
\(\frac{{\sin \alpha }}{{13.8346…}} = \frac{{\sin 40^\circ }}{{10.0111…}}\) (M1)
Note: Award (M1) for correct substitution in the correct sine formula.
α = 62.7° (62.6589) (A1)(ft)
Note: Accept 62.5° from use of 3sf.
\({\text{D}}{\operatorname {\hat B}}{\text{C}}\) = 117(117.341…) (A1)(ft)
Note: Follow through from their part (a). Use of radians results in unrealistic answer, award a maximum of (A1)(M1)(A0)(A0).[4 marks]
Units are required in part (c) only.
\({\text{ABDC}} = \frac{1}{2}(5)(7)\sin 112^\circ + \frac{1}{2}(6)(10.0111…)\sin 117.341…^\circ \) (M1)(A1)(ft)(M1)N
Note: Award (M1) for substitution in both triangle area formulae, (A1)(ft) for their correct substitutions, (M1) for seen or implied addition of their two triangle areas. Follow through from their answer to part (a) and (b).
= 42.9 m2 (42.9039…) (A1)(ft)(G3)
Notes: Answer is 42.9 m2 i.e. the units are required for the final (A1)(ft) to be awarded. Accept 43.0 m2 from using 3sf answers to parts (a) and (b). Do not penalize if use of radians was previously penalized.[4 marks]
Units are required in part (c) only.
42.9039… × 0.5 (M1)(M1)
Note: Award (M1) for 0.5 seen (or equivalent), (M1) for multiplication of their answer in part (c) with their value for depth.
= 21.5 (m3) (21.4519…) (A1)(ft)(G3)
Note: Follow through from their part (c) only if working is seen. Do not penalize if use of radians was previously penalized. Award at most (A0)(M1)(A0)(ft) for multiplying by 50.[3 marks]
Units are required in part (c) only.
(i) π(0.15)2(0.4) (M1)(A1)
OR
π × 152 × 40 (28274.3…) (M1)(A1)
Notes: Award (M1) for substitution in the correct volume formula. (A1) for correct substitutions.
= 0.0283 (m3) (0.0282743…, 0.09π)
(ii) \(\frac{{21.4519…}}{{0.0282743…}}\) (M1)
Note: Award (M1) for correct division of their volumes.
= 759 (A1)(ft)(G2)
Notes: Follow through from their parts (d) and (e)(i). Accept 760 from use of 3sf answers. Answer must be a positive integer for the final (A1)(ft) mark to be awarded.[5 marks]
Question
George leaves a cup of hot coffee to cool and measures its temperature every minute. His results are shown in the table below.
Write down the decrease in the temperature of the coffee
(i) during the first minute (between t = 0 and t =1) ;
(ii) during the second minute;
(iii) during the third minute.[3]
Assuming the pattern in the answers to part (a) continues, show that \(k = 19\).[2]
Use the seven results in the table to draw a graph that shows how the temperature of the coffee changes during the first six minutes.
Use a scale of 2 cm to represent 1 minute on the horizontal axis and 1 cm to represent 10 °C on the vertical axis.[4]
The function that models the change in temperature of the coffee is y = p (2−t )+ q.
(i) Use the values t = 0 and y = 94 to form an equation in p and q.
(ii) Use the values t =1 and y = 54 to form a second equation in p and q.[2]
Solve the equations found in part (d) to find the value of p and the value of q.[2]
The graph of this function has a horizontal asymptote.
Write down the equation of this asymptote.[2]
George decides to model the change in temperature of the coffee with a linear function using correlation and linear regression.
Use the seven results in the table to write down
(i) the correlation coefficient;
(ii) the equation of the regression line y on t.[4]
Use the equation of the regression line to estimate the temperature of the coffee at t = 3.[2]
Find the percentage error in this estimate of the temperature of the coffee at t = 3.[2]
Answer/Explanation
Markscheme
(i) 40
(ii) 20
(iii) 10 (A3)
Notes: Award (A0)(A1)(ft)(A1)(ft) for −40, −20, −10.
Award (A1)(A0)(A1)(ft) for 40, 60, 70 seen.
Award (A0)(A0)(A1)(ft) for −40, −60, −70 seen.
\(24 – k = 5\) or equivalent (A1)(M1)
Note: Award (A1) for 5 seen, (M1) for difference from 24 indicated.
\(k = 19\) (AG)
Note: If 19 is not seen award at most (A1)(M0).
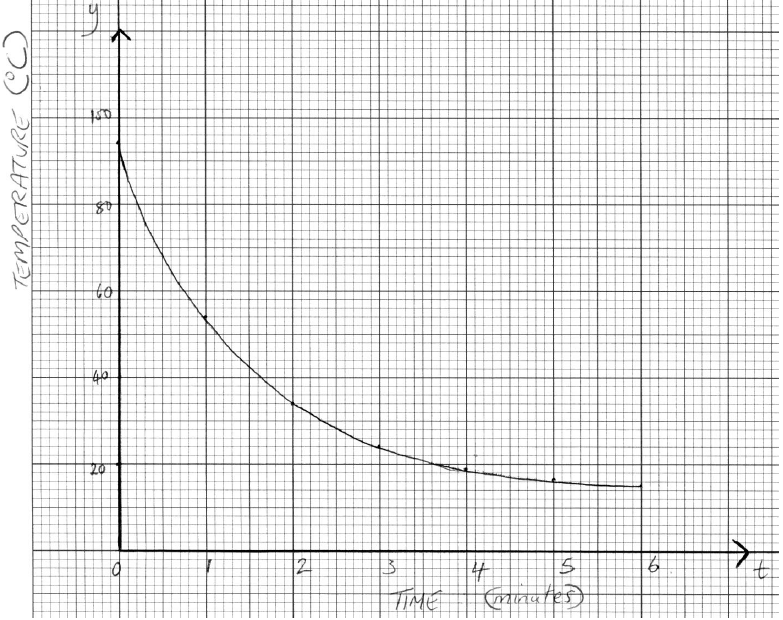(A1)(A1)(A1)(A1)
Note: Award (A1) for scales and labelled axes (t or “time” and y or “temperature”).
Accept the use of x on the horizontal axis only if “time” is also seen as the label.
Award (A2) for all seven points accurately plotted, award (A1) for 5 or 6 points accurately plotted, award (A0) for 4 points or fewer accurately plotted.
Award (A1) for smooth curve that passes through all points on domain [0, 6].
If graph paper is not used or one or more scales is missing, award a maximum of (A0)(A0)(A0)(A1).
(i) \(94 = p + q\) (A1)
(ii) \(54 = 0.5p + q\) (A1)
Note: The equations need not be simplified; accept, for example \(94 = p(2^{-0}) + q\).
p = 80, q = 14 (G1)(G1)(ft)
Note: If the equations have been incorrectly simplified, follow through even if no working is shown.
y = 14 (A1)(A1)(ft)
Note: Award (A1) for y = a constant, (A1) for their 14. Follow through from part (e) only if their q lies between 0 and 15.25 inclusive.
(i) –0.878 (–0.87787…) (G2)
Note: Award (G1) if –0.877 seen only. If negative sign omitted award a maximum of (A1)(A0).
(ii) y = –11.7t + 71.6 (y = –11.6517…t + 71.6336…) (G1)(G1)
Note: Award (G1) for –11.7t, (G1) for 71.6.
If y = is omitted award at most (G0)(G1).
If the use of x in part (c) has not been penalized (the axis has been labelled “time”) then award at most (G0)(G1).
−11.6517…(3) + 71.6339… (M1)
Note: Award (M1) for correct substitution in their part (g)(ii).
= 36.7 (36.6785…) (A1)(ft)(G2)
Note: Follow through from part (g). Accept 36.5 for use of the 3sf answers from part (g).
\(\frac{{36.6785… – 24}}{{24}} \times 100\) (M1)
Note: Award (M1) for their correct substitution in percentage error formula.
= 52.8% (52.82738…) (A1)(ft)(G2)
Note: Follow through from part (h). Accept 52.1% for use of 36.5.
Accept 52.9 % for use of 36.7. If partial working (\(\times 100\) omitted) is followed by their correct answer award (M1)(A1). If partial working is followed by an incorrect answer award (M0)(A0). The percentage sign is not required.
Question
A greenhouse ABCDPQ is constructed on a rectangular concrete base ABCD and is made of glass. Its shape is a right prism, with cross section, ABQ, an isosceles triangle. The length of BC is 50 m, the length of AB is 10 m and the size of angle QBA is 35°.
Write down the size of angle AQB.[1]
Calculate the length of AQ.[3]
Calculate the length of AC.[2]
Show that the length of CQ is 50.37 m, correct to 4 significant figures.[2]
Find the size of the angle AQC.[3]
Calculate the total area of the glass needed to construct
(i) the two rectangular faces of the greenhouse;
(ii) the two triangular faces of the greenhouse.[5]
The cost of one square metre of glass used to construct the greenhouse is 4.80 USD.
Calculate the cost of glass to make the greenhouse. Give your answer correct to the nearest 100 USD.[3]
Answer/Explanation
Answer/Explanation
Markscheme
110° (A1)
\(\frac{{AQ}}{{\sin 35^\circ }} = \frac{{10}}{{\sin 110^\circ }}\) (M1)(A1)
Note: Award (M1) for substituted sine rule formula, (A1) for their correct substitutions.
OR
\(AQ = \frac{5}{{\cos 35^\circ }}\) (A1)(M1)
Note: Award (A1) for 5 seen, (M1) for correctly substituted trigonometric ratio.
\(AQ = 6.10\) (6.10387…) (A1)(ft)(G2)
Notes: Follow through from their answer to part (a).
\(AC^2 = 10^2 + 50^2\) (M1)
Note: Award (M1) for correctly substituted Pythagoras formula.
\(AC = 51.0 (\sqrt{2600}, 50.9901…)\) (A1)(G2)
\(QC^2 = (6.10387…)^2 + (50)^2\) (M1)
Note: Award (M1) for correctly substituted Pythagoras formula.
\(QC = 50.3711…\) (A1)
\(= 50.37\) (AG)
Note: Both the unrounded and rounded answers must be seen to award (A1).
If 6.10 is used then 50.3707… is the unrounded answer.
For an incorrect follow through from part (b) award a maximum of (M1)(A0) – the given answer must be reached to award the final (A1)(AG).
\(\cos AQC = \frac{{{{(6.10387…)}^2} + {{(50.3711…)}^2} – {{(50.9901…)}^2}}}{{2(6.10387…)(50.3711…)}}\) (M1)(A1)(ft)
Note: Award (M1) for substituted cosine rule formula, (A1)(ft) for their correct substitutions.
= 92.4° (\({92.3753…^\circ }\)) (A1)(ft)(G2)
Notes: Follow through from their answers to parts (b), (c) and (d). Accept 92.2 if the 3 sf answers to parts (b), (c) and (d) are used.
Accept 92.5° (\({92.4858…^\circ }\)) if the 3 sf answers to parts (b), (c) and 4 sf answers to part (d) used.
(i) \(2(50 \times 6.10387…)\) (M1)
Note: Award (M1) for their correctly substituted rectangular area formula, the area of one rectangle is not sufficient.
= 610 m2 (610.387…) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b).
The answer is 610 m2. The units are required.
(ii) Area of triangular face \( = \frac{1}{2} \times 10 \times 6.10387… \times \sin 35^\circ \) (M1)(A1)(ft)
OR
Area of triangular face \( = \frac{1}{2} \times 6.10387… \times 6.10387… \times \sin 110^\circ \) (M1)(A1)(ft)
\(= 17.5051…\)
Note: Award (M1) for substituted triangle area formula, (A1)(ft) for correct substitutions.
OR
(Height of triangle) \( = {(6.10387…)^2} – {5^2}\)
\(= 3.50103…\)
Area of triangular face \( = \frac{1}{2} \times 10 \times their{\text{ }} height\)
\(= 17.5051…\)
Note: Award (M1) for substituted triangle area formula, (A1)(ft) for correctly substituted area formula. If 6.1 is used, the height is 3.49428… and the area of both triangular faces 34.9 m2
Area of both triangular faces = 35.0 m2 (35.0103…) (A1)(ft)(G2)
Notes: The answer is 35.0 m2. The units are required. Do not penalize if already penalized in part (f)(i). Follow through from their part (b).
(610.387… + 35.0103…) × 4.80 (M1)
= 3097.90… (A1)(ft)
Notes: Follow through from their answers to parts (f)(i) and (f)(ii).
Accept 3096 if the 3 sf answers to part (f) are used.
= 3100 (A1)(ft)(G2)
Notes: Follow through from their unrounded answer, irrespective of whether it is correct. Award (M1)(A2) if working is shown and 3100 seen without the unrounded answer being given.
Question
Give all answers in this question correct to two decimal places.
Arthur lives in London. On \({1^{{\text{st}}}}\) August 2008 Arthur paid \({\text{37}}\,{\text{500}}\) euros (\({\text{EUR}}\)) for a new car from Germany. The price of the same car in London was \({\text{34}}\,{\text{075}}\) British pounds (\({\text{GBP}}\)).
The exchange rate on \({1^{{\text{st}}}}\) August 2008 was \({\text{1}}\,{\text{EUR = 0.7234}}\,{\text{GBP}}\).
Calculate, in GBP, the price that Arthur paid for the car.[2]
Write down, in \({\text{GBP}}\), the amount of money Arthur saved by buying the car in Germany.[1]
Between \({1^{{\text{st}}}}\) August 2008 and \({1^{{\text{st}}}}\) August 2012 Arthur’s car depreciated at an annual rate of \(9\%\) of its current value.
Calculate the value, in \({\text{GBP}}\), of Arthur’s car on \({1^{{\text{st}}}}\) August 2009.[3]
Between \({1^{{\text{st}}}}\) August 2008 and \({1^{{\text{st}}}}\) August 2012 Arthur’s car depreciated at an annual rate of \(9\%\) of its current value.
Show that the value of Arthur’s car on \({1^{{\text{st}}}}\) August 2012 was \({\text{18}}\,{\text{600}}\,{\text{GBP}}\), correct to the nearest \({\text{100}}\,{\text{GBP}}\).[3]
Answer/Explanation
Markscheme
The first answer not given to two decimal places is not awarded the final (A1). Incorrect rounding is not penalized thereafter.
\(37\,500 \times 0.7234\) (M1)
\( = 27\,127.50\) (A1)(G2)[2 marks]
The first answer not given to two decimal places is not awarded the final (A1). Incorrect rounding is not penalized thereafter.
\(6947.50\) (A1)(ft)(G1)
Note: Follow through from part (a) irrespective of whether working is seen.
[1 mark]
The first answer not given to two decimal places is not awarded the final (A1). Incorrect rounding is not penalized thereafter.
\(27\,127.50 \times 0.91\) (A1)(M1)
Note: Award (A1) for \(0.91\) seen or equivalent, (M1) for their \({\text{27}}\,{\text{127.50}}\) multiplied by \(0.91\)
OR
\(27\,127.50 – 0.09 \times 27\,127.50\) (A1)(M1)
Note: Award (A1) for \(0.09 \times 27\,127.50\) seen, and (M1) for \(27\,127.50 – 0.09 \times 27\,127.50\).
\( = 24\,686.03\) (A1)(ft)(G2)
Note: Follow through from part (a).[3 marks]
The first answer not given to two decimal places is not awarded the final (A1). Incorrect rounding is not penalized thereafter.
\(27\,127.50 \times {\left( {1 – \frac{9}{{100}}} \right)^4}\) (M1)(A1)(ft)
Notes: Award (M1) for substituted compound interest formula, (A1)(ft) for correct substitution.
Follow through from part (a).
OR
\(27\,127.50 \times {(0.91)^4}\) (M1)(A1)(ft)
Notes: Award (M1) for substituted geometric sequence formula, (A1)(ft) for correct substitution.
Follow through from part (a).
OR (lists (i))
\({\text{24}}\,{\text{686.03, 22}}\,{\text{464.28…, 20}}\,{\text{442.50…, 18}}\,{\text{602.67…}}\) (M1)(A1)(ft)
Notes: Award (M1) for at least the \({{\text{2}}^{{\text{nd}}}}\) term correct (calculated from their \(({\text{a}}) \times 0.91\)). Award (A1)(ft) for four correct terms (rounded or unrounded).
Follow through from part (a).
Accept list containing the last three terms only (\({\text{24}}\,{\text{686.03}}\) may be implied).
OR (lists(ii))
\(27\,127.50 – (2441.47… + 2221.74… + 2021.79… + 1839.82…)\) (M1)(A1)(ft)
Notes: Award (M1) for subtraction of four terms from \({\text{27}}\,{\text{127.50}}\).
Award (A1) for four correct terms (rounded or unrounded).
Follow through from part (a).
\( = 18\,602.67\) (A1)
\( = 18\,600\) (AG)
Note: The final (A1) is not awarded unless both the unrounded and rounded answers are seen.[3 marks]
Question
A cross-country running course consists of a beach section and a forest section. Competitors run from \({\text{A}}\) to \({\text{B}}\), then from \({\text{B}}\) to \({\text{C}}\) and from \({\text{C}}\) back to \({\text{A}}\).
The running course from \({\text{A}}\) to \({\text{B}}\) is along the beach, while the course from \({\text{B}}\), through \({\text{C}}\) and back to \({\text{A}}\), is through the forest.
The course is shown on the following diagram.
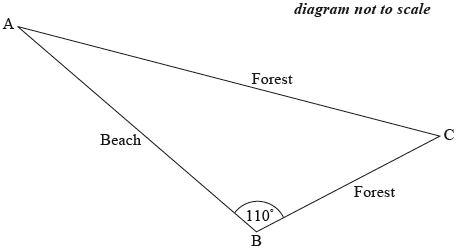
Angle \({\text{ABC}}\) is \(110^\circ\).
It takes Sarah \(5\) minutes and \(20\) seconds to run from \({\text{A}}\) to \({\text{B}}\) at a speed of \(3.8{\text{ m}}{{\text{s}}^{ – 1}}\).
Using ‘distance = speed \( \times \) time’, show that the distance from \({\text{A}}\) to \({\text{B}}\) is \(1220\) metres correct to 3 significant figures.[2]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the speed, in \({\text{m}}{{\text{s}}^{ – 1}}\), that Sarah runs from \({\text{B}}\) to \({\text{C}}\).[1]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the distance, in metres, from \({\mathbf{C}}\) to \({\mathbf{A}}\).[3]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the total distance, in metres, of the cross-country running course.[2]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Find the size of angle \({\text{BCA}}\).[3]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the area of the cross-country course bounded by the lines \({\text{AB}}\), \({\text{BC}}\) and \({\text{CA}}\).[3]
Answer/Explanation
Markscheme
\(3.8 \times 320\) (A1)
Note: Award (A1) for \(320\) or equivalent seen.
\( = 1216\) (A1)
\( = 1220{\text{ (m)}}\) (AG)
Note: Both unrounded and rounded answer must be seen for the final (A1) to be awarded.[2 marks]
\(\frac{{850}}{{303}}{\text{ (m}}{{\text{s}}^{ – 1}}){\text{ (2.81, 2.80528}} \ldots {\text{)}}\) (A1)(G1)[1 mark]
\({\text{A}}{{\text{C}}^2} = {1220^2} + {850^2} – 2(1220)(850)\cos 110^\circ \) (M1)(A1)
Note: Award (M1) for substitution into cosine rule formula, (A1) for correct substitutions.
\({\text{AC}} = 1710{\text{ (m) (1708.87}} \ldots {\text{)}}\) (A1)(G2)
Notes: Accept \(1705{\text{ }} (1705.33…)\).[3 marks]
\(1220 + 850 + {\text{1708.87}} \ldots \) (M1)
\( = {\text{3780 (m) (3778.87}} \ldots {\text{)}}\) (A1)(ft)(G1)
Notes: Award (M1) for adding the three sides. Follow through from their answer to part (c). Accept \(3771{\text{ }} (3771.33…)\).[2 marks]
\(\frac{{\sin C}}{{1220}} = \frac{{\sin 110^\circ }}{{{\text{1708.87}} \ldots }}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into sine rule formula, (A1)(ft) for correct substitutions. Follow through from their part (c).
\(C = 42.1^\circ {\text{ (42.1339}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Accept \(41.9^{\circ}, 42.0^{\circ}, 42.2^{\circ}, 42.3^{\circ}\).
OR
\(\cos C = \frac{{{\text{1708.87}}{ \ldots ^2} + {{850}^2} – {{1220}^2}}}{{2 \times {\text{1708.87}} \ldots \times 850}}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into cosine rule formula, (A1)(ft) for correct substitutions. Follow through from their part (c).
\(C = 42.1^\circ {\text{ (42.1339}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Accept \(41.2^{\circ}, 41.8^{\circ}, 42.4^{\circ}\).[3 marks]
\(\frac{1}{2} \times 1220 \times 850 \times \sin 110^\circ \) (M1)(A1)(ft)
OR
\(\frac{1}{2} \times {\text{1708.87}} \ldots \times 850 \times \sin {\text{42.1339}} \ldots ^\circ \) (M1)(A1)(ft)
OR
\(\frac{1}{2} \times 1220 \times {\text{1708.87}} \ldots \times \sin {\text{27.8661}} \ldots ^\circ \) (M1)(A1)(ft)
Note: Award (M1) for substitution into area formula, (A1)(ft) for correct substitution.
\( = 487\,000{\text{ }}{{\text{m}}^2}{\text{ (487}}\,{\text{230}} \ldots {\text{ }}{{\text{m}}^2})\) (A1)(ft)(G2)
Notes: The answer is \(487\,000{\text{ }}{{\text{m}}^2}\), units are required.
Accept \(486\,000{\text{ }}{{\text{m}}^2}{\text{ (485}}\,{\text{633}} \ldots {\text{ }}{{\text{m}}^2})\).
If workings are not shown and units omitted, award (G1) for \(487\,000{\text{ or }}486\,000\).
Follow through from parts (c) and (e).[3 marks]
Question
Give your answers to parts (a) to (e) to the nearest dollar.
On Hugh’s 18th birthday his parents gave him options of how he might receive his monthly allowance for the next two years.
Option A \(\$60\) each month for two years
Option B \(\$10\) in the first month, \(\$15\) in the second month, \(\$20\) in the third month, increasing by \(\$5\) each month for two years
Option C \(\$15\) in the first month and increasing by \(10\%\) each month for two years
Option D Investing \(\$1500\) at a bank at the beginning of the first year, with an interest rate of \(6\%\) per annum, compounded monthly.
Hugh does not spend any of his allowance during the two year period.
If Hugh chooses Option A, calculate the total value of his allowance at the end of the two year period.[2]
If Hugh chooses Option B, calculate
(i) the amount of money he will receive in the 17th month;
(ii) the total value of his allowance at the end of the two year period.[5]
If Hugh chooses Option C, calculate
(i) the amount of money Hugh would receive in the 13th month;
(ii) the total value of his allowance at the end of the two year period.[5]
If Hugh chooses Option D, calculate the total value of his allowance at the end of the two year period.[3]
State which of the options, A, B, C or D, Hugh should choose to give him the greatest total value of his allowance at the end of the two year period.[1]
Another bank guarantees Hugh an amount of \(\$1750\) after two years of investment if he invests $1500 at this bank. The interest is compounded annually.
Calculate the interest rate per annum offered by the bank.[3]
Answer/Explanation
Markscheme
The first time an answer is not given to the nearest dollar in parts (a) to (e), the final (A1) in that part is not awarded.
\(60 \times 24\) (M1)
Note: Award (M1) for correct product.
\( = 1440\) (A1)(G2)[2 marks]
The first time an answer is not given to the nearest dollar in parts (a) to (e), the final (A1) in that part is not awarded.
(i) \(10 + (17 – 1)(5)\) (M1)(A1)
Note: Award (M1) for substituted arithmetic sequence formula, (A1) for correct substitution.
\( = 90\) (A1)(G2)
(ii) \(\frac{{24}}{2}\left( {2(10) + (24 – 1)(5)} \right)\) (M1)
OR
\(\frac{{24}}{2}\left( {10 + 125} \right)\) (M1)
Note: Award (M1) for correct substitution in arithmetic series formula.
\( = 1620\) (A1)(ft)(G1)
Note: Follow through from part (b)(i).[5 marks]
The first time an answer is not given to the nearest dollar in parts (a) to (e), the final (A1) in that part is not awarded.
(i) \(15{(1.1)^{12}}\) (M1)(A1)
Note: Award (M1) for substituted geometric sequence formula, (A1) for correct substitutions.
\( = 47\) (A1)(G2)
Note: Award (M1)(A1)(A0) for \(47.08\).
Award (G1) for \(47.08\) if workings are not shown.
(ii) \(\frac{{15({{1.1}^{24}} – 1)}}{{1.1 – 1}}\) (M1)
Note: Award (M1) for correct substitution in geometric series formula.
\( = 1327\) (A1)(ft)(G1)
Note: Follow through from part (c)(i).[5 marks]
The first time an answer is not given to the nearest dollar in parts (a) to (e), the final (A1) in that part is not awarded.
\(1500{\left( {1 + \frac{6}{{100(12)}}} \right)^{12(2)}}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula, (A1) for correct substitutions.
OR
\(N = 2\)
\(I\% = 6\)
\(PV = 1500\)
\(P/Y = 1\)
\(C/Y = 12\) (A1)(M1)
Note: Award (A1) for \(C/Y = 12\) seen, (M1) for other correct entries.
OR
\(N = 24\)
\(I\% = 6\)
\(PV = 1500\)
\(P/Y = 12\)
\(C/Y = 12\) (A1)(M1)
Note: Award (A1) for \(C/Y = 12\) seen, (M1) for other correct entries.
\( = 1691\) (A1)(G2)[3 marks]
The first time an answer is not given to the nearest dollar in parts (a) to (e), the final (A1) in that part is not awarded.
Option D (A1)(ft)
Note: Follow through from their parts (a), (b), (c) and (d). Award (A1)(ft) only if values for the four options are seen and only if their answer is consistent with their parts (a), (b), (c) and (d).[1 mark]
\(1750 = 1500{\left( {1 + \frac{r}{{100}}} \right)^2}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula equated to \(1750\), (A1) for correct substitutions into formula.
OR
\(N = 2\)
\(PV = 1500\)
\(FV = – 1750\)
\(P/Y = 1\)
\(C/Y = 1\) (A1)(M1)
Note: Award (A1) for \(FV = 1750\) seen, (M1) for other correct entries.
\( = 8.01\% {\text{ (8.01234}} \ldots \% ,{\text{ }}0.0801{\text{)}}\) (A1)(G2)[3 marks]
Question
In a game, n small pumpkins are placed 1 metre apart in a straight line. Players start 3 metres before the first pumpkin.
Each player collects a single pumpkin by picking it up and bringing it back to the start. The nearest pumpkin is collected first. The player then collects the next nearest pumpkin and the game continues in this way until the signal is given for the end.
Sirma runs to get each pumpkin and brings it back to the start.
Write down the distance, \({a_1}\), in metres that she has to run in order to collect the first pumpkin.[1]
The distances she runs to collect each pumpkin form a sequence \({a_1},{\text{ }}{a_2},{\text{ }}{a_3}, \ldots \) .
(i) Find \({a_2}\).
(ii) Find \({a_3}\).[2]
Write down the common difference, \(d\), of the sequence.[1]
The final pumpkin Sirma collected was 24 metres from the start.
(i) Find the total number of pumpkins that Sirma collected.
(ii) Find the total distance that Sirma ran to collect these pumpkins.[5]
Peter also plays the game. When the signal is given for the end of the game he has run 940 metres.
Calculate the total number of pumpkins that Peter collected.[3]
Peter also plays the game. When the signal is given for the end of the game he has run 940 metres.
Calculate Peter’s distance from the start when the signal is given.[2]
Answer/Explanation
Markscheme
\(6{\text{ (m)}}\) (A1)(G1)
(i) \(8\) (A1)(ft)
(ii) \(10\) (A1)(ft)(G2)
Note: Follow through from part (a).
\(2{\text{ (m)}}\) (A1)(ft)
Note: Follow through from parts (a) and (b).
(i) \(2 \times 24 = 6 + 2(n – 1)\;\;\;\)OR\(\;\;\;24 = 3 + (n – 1)\) (M1)
Note: Award (M1) for correct substitution in arithmetic sequence formula.
\(n = 22\) (A1)(ft)(G1)
Note: Follow through from parts (a) and (c).
(ii) \(\frac{{(6 + 48)}}{2} \times 22\) (M1)(A1)(ft)
Note: Award (M1) for substitution in arithmetic series formula, (A1)(ft) for correct substitution.
\( = 594\) (A1)(ft)(G2)
Note: Follow through from parts (a) and (d)(i).
\(\frac{{\left[ {2 \times 6 + 2(n – 1)} \right] \times n}}{2} = 940\) (M1)(A1)(ft)
Notes: Award (M1) for substitution in arithmetic series formula, (A1) for their correct substituted formula equated to \(940\). Follow through from parts (a) and (c).
\({n^2} + 5n – 940 = 0\)
\(n = 28.2611 \ldots \)
\(n = 28\) (A1)(ft)(G2)
\(\frac{{\left[ {2 \times 6 + 2(28 – 1)} \right] \times 28}}{2}\) (M1)
Notes: Award (M1) for substituting their \(28\) into the arithmetic series formula.
\( = 16{\text{ (m)}}\) (A1)(ft)(G2)
Question
A boat race takes place around a triangular course, \({\text{ABC}}\), with \({\text{AB}} = 700{\text{ m}}\), \({\text{BC}} = 900{\text{ m}}\) and angle \({\text{ABC}} = 110^\circ \). The race starts and finishes at point \({\text{A}}\).
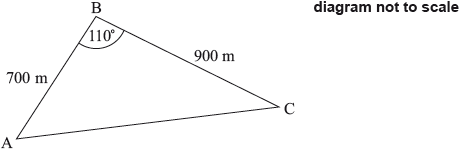
Calculate the total length of the course.[4]
It is estimated that the fastest boat in the race can travel at an average speed of \(1.5\;{\text{m}}\,{{\text{s}}^{ – 1}}\).
Calculate an estimate of the winning time of the race. Give your answer to the nearest minute.[3]
It is estimated that the fastest boat in the race can travel at an average speed of \(1.5\;{\text{m}}\,{{\text{s}}^{ – 1}}\).
Find the size of angle \({\text{ACB}}\).[3]
To comply with safety regulations, the area inside the triangular course must be kept clear of other boats, and the shortest distance from \({\text{B}}\) to \({\text{AC}}\) must be greater than \(375\) metres.
Calculate the area that must be kept clear of boats.[3]
To comply with safety regulations, the area inside the triangular course must be kept clear of other boats, and the shortest distance from \({\text{B}}\) to \({\text{AC}}\) must be greater than \(375\) metres.
Determine, giving a reason, whether the course complies with the safety regulations.[3]
The race is filmed from a helicopter, \({\text{H}}\), which is flying vertically above point \({\text{A}}\).
The angle of elevation of \({\text{H}}\) from \({\text{B}}\) is \(15^\circ\).
Calculate the vertical height, \({\text{AH}}\), of the helicopter above \({\text{A}}\).[2]
The race is filmed from a helicopter, \({\text{H}}\), which is flying vertically above point \({\text{A}}\).
The angle of elevation of \({\text{H}}\) from \({\text{B}}\) is \(15^\circ\).
Calculate the maximum possible distance from the helicopter to a boat on the course.[3]
Answer/Explanation
Markscheme
\({\text{A}}{{\text{C}}^2} = {700^2} + {900^2} – 2 \times 700 \times 900 \times \cos 110^\circ \) (M1)(A1)
\({\text{AC}} = 1315.65 \ldots \) (A1)(G2)
length of course \( = 2920{\text{ (m)}}\;\;\;(2915.65 \ldots {\text{ m)}}\) (A1)
Notes: Award (M1) for substitution into cosine rule formula, (A1) for correct substitution, (A1) for correct answer.
Award (G3) for \(2920\;\;\;(2915.65 \ldots )\) seen without working.
The final (A1) is awarded for adding \(900\) and \(700\) to their \({\text{AC}}\) irrespective of working seen.
\(\frac{{2915.65}}{{1.5}}\) (M1)
Note: Award (M1) for their length of course divided by \(1.5\).
Follow through from part (a).
\( = 1943.76 \ldots {\text{ (seconds)}}\) (A1)(ft)
\( = 32{\text{ (minutes)}}\) (A1)(ft)(G2)
Notes: Award the final (A1) for correct conversion of their answer in seconds to minutes, correct to the nearest minute.
Follow through from part (a).
\(\frac{{700}}{{\sin {\text{ACB}}}} = \frac{{1315.65 \ldots }}{{\sin 110^\circ }}\) (M1)(A1)(ft)
OR
\(\cos {\text{ACB}} = \frac{{{{900}^2} + 1315.65{ \ldots ^2} – {{700}^2}}}{{2 \times 900 \times 1315.65 \ldots }}\) (M1)(A1)(ft)
\({\text{ACB}} = 30.0^\circ \;\;\;(29.9979 \ldots ^\circ )\) (A1)(ft)(G2)
Notes: Award (M1) for substitution into sine rule or cosine rule formula, (A1) for their correct substitution, (A1) for correct answer.
Accept \(29.9^\circ\) for sine rule and \(29.8^\circ\) for cosine rule from use of correct three significant figure values. Follow through from their answer to (a).
\(\frac{1}{2} \times 700 \times 900 \times \sin 110^\circ \) (M1)(A1)
Note: Accept \(\frac{1}{2} \times {\text{their AC}} \times {\text{900}} \times {\text{sin(their ACB)}}\). Follow through from parts (a) and (c).
\( = 296000{\text{ }}{{\text{m}}^2}\;\;\;(296003{\text{ }}{{\text{m}}^2})\) (A1)(G2)
Notes: Award (M1) for substitution into area of triangle formula, (A1) for correct substitution, (A1) for correct answer.
Award (G1) if \(296000\) is seen without units or working.
\(\sin 29.9979 \ldots = \frac{{{\text{distance}}}}{{900}}\) (M1)
\({\text{(distance}} = ){\text{ }}450{\text{ (m)}}\;\;\;{\text{(449.971}} \ldots {\text{)}}\) (A1)(ft)(G2)
Note: Follow through from part (c).
OR
\(\frac{1}{2} \times {\text{distance}} \times 1315.65 \ldots = 296003\) (M1)
\(({\text{distance}} = ){\text{ }}450{\text{ (m)}}\;\;\;{\text{(449.971}} \ldots {\text{)}}\) (A1)(ft)(G2)
Note: Follow through from part (a) and part (d).
\(450\) is greater than \(375\), thus the course complies with the safety regulations (R1)
Notes: A comparison of their area from (d) and the area resulting from the use of \(375\) as the perpendicular distance is a valid approach and should be given full credit. Similarly a comparison of angle \({\text{ACB}}\) and \({\sin ^{ – 1}}\left( {\frac{{375}}{{900}}} \right)\) should be given full credit.
Award (R0) for correct answer without any working seen. Award (R1)(ft) for a justified reason consistent with their working.
Do not award (M0)(A0)(R1).
\(\tan 15^\circ = \frac{{{\text{AH}}}}{{700}}\) (M1)
Note: Award (M1) for correct substitution into trig formula.
\({\text{AH}} = 188{\text{ (m)}}\;\;\;(187.564 \ldots )\) (A1)(ft)(G2)
\({\text{H}}{{\text{C}}^2} = 187.564{ \ldots ^2} + 1315.65{ \ldots ^2}\) (M1)(A1)
Note: Award (M1) for substitution into Pythagoras, (A1) for their \(1315.65{ \ldots}\) and their \(187.564{ \ldots}\) correctly substituted in formula.
\({\text{HC}} = 1330 \ldots {\text{ (m)}}\;\;\;(1328.95 \ldots )\) (A1)(ft)(G2)
Note: Follow through from their answer to parts (a) and (f).