Question
Calculate \(\frac{{77.2 \times {3^3}}}{{3.60 \times {2^2}}}\).
Express your answer to part (a) in the form \(a \times 10^k\), where \(1 \leqslant a < 10\) and \(k \in {\mathbb{Z}}\).
Juan estimates the length of a carpet to be 12 metres and the width to be 8 metres. He then estimates the area of the carpet.
(i) Write down his estimated area of the carpet.
When the carpet is accurately measured it is found to have an area of 90 square metres.
(ii) Calculate the percentage error made by Juan.
Answer/Explanation
Markscheme
\(144.75\left( { = \frac{{579}}{4}} \right)\) (A1)
accept 145 (C1)
[1 mark]
\(1.4475 \times 10^2\) (A1)(ft)(A1)(ft)
accept \(1.45 \times 10^2\) (C2)
[2 marks]
Unit penalty (UP) is applicable in question part (c)(i) only.
(UP) (i) Area = 96 m2 (A1)
(ii) \(\% {\text{ error}} = \frac{{(96 – 90)}}{{90}} \times 100\) (M1)
\( = \frac{{6 \times 100}}{{90}}\)
\(\frac{{20}}{3}\% \) or 6.67 % (A1)(ft) (C3)
[3 marks]
Question
Calculate exactly \(\frac{{{{(3 \times 2.1)}^3}}}{{7 \times 1.2}}\).
Write the answer to part (a) correct to 2 significant figures.
Calculate the percentage error when the answer to part (a) is written correct to 2 significant figures.
Write your answer to part (c) in the form \(a \times {10^k}\) where \(1 \leqslant a < 10{\text{ and }}k \in \mathbb{Z}\).
Answer/Explanation
Markscheme
\(29.7675\) (A1) (C1)
Note: Accept exact answer only.
[1 mark]
\(30\) (A1)(ft) (C1)
[1 mark]
\(\frac{{30 – 29.7675}}{{29.7675}} \times 100\% \) (M1)
For correct formula with correct substitution.
\( = 0.781\% \) accept \(0.78\% \) only if formula seen with \(29.7675\) as denominator (A1)(ft) (C2)
[2 marks]
\(7.81 \times {10^{ – 1}}\% \) (\(7.81 \times {10^{ – 3}}\) with no percentage sign) (A1)(ft)(A1)(ft) (C2)
[2 marks]
Question
Given that \(h = \sqrt {{\ell ^2} – \frac{{{d^2}}}{4}} \) ,
Calculate the exact value of \(h\) when \(\ell = 0.03625\) and \(d = 0.05\) .
Write down the answer to part (a) correct to three decimal places.
Write down the answer to part (a) correct to three significant figures.
Write down the answer to part (a) in the form \(a \times {10^k}\) , where \(1 \leqslant a < 10{\text{, }}k \in \mathbb{Z}\).
Answer/Explanation
Markscheme
\(h = \sqrt {{{0.03625}^2} – \frac{{{{0.05}^2}}}{4}} \) (M1)
\( = 0.02625\) (A1) (C2)
Note: Award (A1) only for \(0.0263\) seen without working
[2 marks]
\(0.026\) (A1)(ft) (C1)
[1 mark]
\(0.0263\) (A1)(ft) (C1)
[1 mark]
\(2.625 \times {10^{ – 2}}\)
for \(2.625\) (ft) from unrounded (a) only (A1)(ft)
for \( \times {10^{ – 2}}\) (A1)(ft) (C2)
[2 marks]
Question
Consider the following four numbers.
\(p = 0.00314{\text{ ; }}q = 0.00314 \times {10^2}{\text{ ; }}r = \frac{\pi }{{1000}}{\text{ ; }}s = 3.14 \times {10^{ – 2}}\)
One of these numbers is written in the form \(a \times {10^k}\) where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\). Write down this number.
Write down the smallest of these numbers.
Write down the value of q + s.
Give your answer to part (c) in the form \(a \times {10^k}\) where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\).
Answer/Explanation
Markscheme
3.14 × 10–2 or s (A1) (C1)
[1 mark]
0.00314 or 3.14 × 10–3 or p (M1)(A1) (C2)
Note: Award (M1) for indication of comparing numbers where at least one of them is converted. The converted number does not have to be correct. A single converted number is sufficient for (M1) to be awarded.
[2 marks]
0.3454 (0.345) (A1) (C1)
[1 mark]
3.454 × 10–1 (3.45 × 10–1) (A1)(A1)(ft) (C2)
Notes: Follow through from their (c).
Award (A1) for 3.454 (3.45) (A1) for 10–1.
[2 marks]
Question
In a television show there is a transparent box completely filled with identical cubes. Participants have to estimate the number of cubes in the box. The box is 50 cm wide, 100 cm long and 40 cm tall.
Find the volume of the box.
Joaquin estimates the volume of one cube to be 500 cm3. He uses this value to estimate the number of cubes in the box.
Find Joaquin’s estimated number of cubes in the box.
The actual number of cubes in the box is 350.
Find the percentage error in Joaquin’s estimated number of cubes in the box.
Answer/Explanation
Markscheme
\(50 \times 100 \times 40 = 200\,000{\text{ c}}{{\text{m}}^3}\) (M1)(A1) (C2)
Note: Award (M1) for correct substitution in the volume formula.
[2 marks]
\(\frac{{200\,000}}{{500}} = 400\) (M1)(A1)(ft) (C2)
Note: Award (M1) for dividing their answer to part (a) by 500.
[2 marks]
\(\frac{{400 – 350}}{{350}} \times 100 = 14.3{\text{ }}\% \) (M1)(A1)(ft) (C2)
Notes: Award (M1) for correct substitution in the percentage error formula.
Award (A1) for answer, follow through from part (b).
Accept –14.3 %.
% sign not necessary.
[2 marks]
Question
Given \(p = x – \frac{{\sqrt y }}{z}\) , \(x = 1.775\) , \(y = 1.44\) and \(z = 48\) .
Calculate the value of \(p\).
Barry first writes \(x\) , \(y\) and \(z\) correct to one significant figure and then uses these values to estimate the value of \(p\) .
(i) Write down \(x\) , \(y\) and \(z\) each correct to one significant figure.
(ii) Write down Barry’s estimate of the value of \(p\) .
Calculate the percentage error in Barry’s estimate of the value of \(p\) .
Answer/Explanation
Markscheme
\(p = 1.775 – \frac{{\sqrt {1.44} }}{{48}}\) (M1)
Note: Award (M1) for correctly substituted equation for \(p\).
\( = 1.75\) \(\left( {1.750{\text{, }}\frac{7}{4}} \right)\) (A1)(C2)
[2 marks]
(i) \(x = 2\), \(y =1\), \(z = 50\) (A1)
(ii) \(p =1.98\) \(\left( {\frac{{99}}{{50}}} \right)\) (A1)(ft) (C2)
Note: Follow through from part (b)(i), irrespective of whether working is shown.
Note: If 2 s.f. used throughout part (b)(i) award (A1)(ft) for \(1.78\) or \(1.8\).
[2 marks]
\(\frac{{1.98 – 1.75}}{{1.75}} \times 100\) (M1)
Note: Award (M1) for correctly substituted \(\% \) error formula.
Note: Follow through from parts (a) and (b).
\( = 13.1\% \) (A1)(ft) (C2)
Notes: \(\% \) sign not required. Do not accept \( – 13.1\% \). If 100 missing and incorrect answer, award (M0)(A0). If 100 missing and answer incorrectly rounded, award (M1)(A1).
[2 marks]
Question
The table below shows the frequency distribution of the number of dental fillings for a group of \(25\) children.

Find the value of \(q\) .
Use your graphic display calculator to find
(i) the mean number of fillings;
(ii) the median number of fillings;
(iii) the standard deviation of the number of fillings.
Answer/Explanation
Markscheme
\(q = 25 – (4 + 3 + 8 + 4 +1)\) (M1)
Note: Award (M1) for subtraction from \(25\) of all values from the table.
\( = 5\) (A1) (C2)
[2 marks]
(i) \(2.2\) (A2)(ft) (C2)
Note: Award (M1) for use of mean formula with correct substitution. Follow through from part (a), irrespective of whether working is shown.
(ii) \(2\) (A1) (C1)
(iii) \(1.39\) (A1)(ft) (C1)
Note: Follow through from part (a), irrespective of whether working is shown. Award (A1) for \(1.38\).
[4 marks]
Question
Ross is a star that is 82 414 080 000 000 km away from Earth. A spacecraft, launched from Earth, travels at 48 000 kmh–1 towards Ross.
Calculate the exact time, in hours, for the spacecraft to reach the star Ross.
Give your answer to part (a) in years. (Assume 1 year = 365 days)
Give your answer to part (b) in the form a×10k, where 1 ≤ a < 10 and \(k \in \mathbb{Z}\).
Answer/Explanation
Markscheme
\(\frac{{{\text{82 414 080 000 000}}}}{{48\;000}}\) (M1)
Note: Award (M1) for correct substitution in correct formula.
1 716 960 000 (hours) (A1) (C2)
[2 marks]
\(\frac{{{\text{their (a)}}}}{{24 \times 365}}\) (M1)
196 000 (years) (A1)(ft) (C2)
Note: Award (A1)(ft) from their part (a).
[2 marks]
1.96×105 (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for 1.96 (accept 1.96000), (A1)(ft) for 105 . Follow through from their answer to part (b).
[2 marks]
Question
Consider c = 5200 and d = 0.0000037.
Write down the value of r = c × d.
Write down your value of r in the form a × 10k, where 1 ≤ a < 10 and \(k \in \mathbb{Z}\).
Consider the following statements about c, d and r. Only three of these statements are true.
Circle the true statements.

Answer/Explanation
Markscheme
r = 0.01924 (A1) (C1)
Note: Accept 0.0192 and 0.019
[1 mark]
r = 1.924 × 10−2 (A1)(ft)(A1)(ft) (C2)
Notes: Award (A1) for 1.924, (A1) for 10−2. Accept 1.92 and 1.9. Follow through from their part (a).
[2 marks]
(A1)(A1)(A1) (C3)
Notes: Award (A1) for each true statement circled. Do not follow through from part (a). Award (A1)(A1)(A0) if 1 extra term seen. Award (A1)(A0)(A0) if 2 extra terms seen. Award (A0)(A0)(A0) if all terms circled. Accept other indications of the correct statements i.e. highlighted or ticks.
[3 marks]
Question
The diagram below represents a rectangular flag with dimensions 150 cm by 92 cm. The flag is divided into three regions A, B and C.
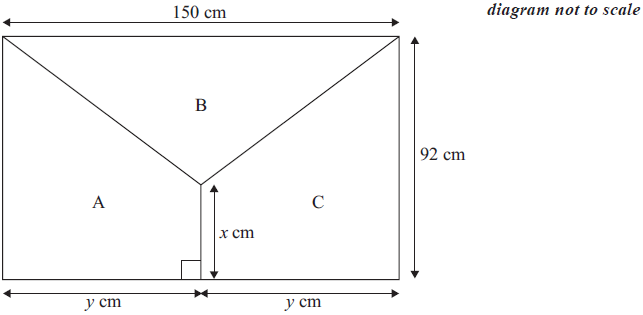
Write down the total area of the flag.
Write down the value of y.
The areas of regions A, B, and C are equal.
Write down the area of region A.
Using your answers to parts (b) and (c), find the value of x.
Answer/Explanation
Markscheme
Units are required in this question for full marks to be awarded.
13800 cm2 (A1) (C1)
75 (A1) (C1)
Units are required in this question for full marks to be awarded.
4600 cm2 (A1)(ft) (C1)
Notes: Units are required unless already penalized in part (a). Follow through from their part (a).
\(0.5(x + 92) \times 75 = 4600\) (M1)(A1)(ft)
OR
\(0.5 \times 150 \times (92 – x) = 4600\) (M1)(A1)(ft)
Note: Award (M1) for substitution into area formula, (A1)(ft) for their correct substitution.
(= 30.7 (cm)(30.6666…(cm)) (A1)(ft) (C3)
Note: Follow through from their parts (b) and (c).
Question
The average radius of the orbit of the Earth around the Sun is 150 million kilometres.
The average radius of the orbit of the Earth around the Sun is 150 million kilometres.

Write down this radius, in kilometres, in the form \(a \times {10^k}\), where \(1 \leqslant a < 10,{\text{ }}k \in \mathbb{Z}\).
The Earth travels around the Sun in one orbit. It takes one year for the Earth to complete one orbit.
Calculate the distance, in kilometres, the Earth travels around the Sun in one orbit, assuming that the orbit is a circle.
Today is Anna’s 17th birthday.
Calculate the total distance that Anna has travelled around the Sun, since she was born.
Answer/Explanation
Markscheme
\(1.5 \times {10^8}{\text{ (km)}}\) (A2) (C2)
Notes: Award (A2) for the correct answer.
Award (A1)(A0) for 1.5 and an incorrect index.
Award (A0)(A0) for answers of the form \(15 \times {10^7}\).
[2 marks]
\(2\pi 1.5 \times {10^8}\) (M1)
\( = 942\,000\,000{\text{ (km) (942}}\,{\text{477}}\,{\text{796.1}} \ldots {\text{, }}3 \times {10^8}\pi ,{\text{ }}9.42 \times {10^8})\) (A1)(ft) (C2)
Notes: Award (M1) for correct substitution into correct formula. Follow through from part (a).
Do not accept calculator notation \(9.42{\text{E}}8\).
Do not accept use of \(\frac{{22}}{7}\) or\( 3.14\) for \(\pi\).
[2 marks]
\(17 \times 942\,000\,000\) (M1)
\( = 1.60 \times {10^{10}}{\text{ (km) }}\left( {{\text{1.60221}} \ldots \times {{10}^{10}}{\text{, 1.6014}} \times {{10}^{10}},{\text{ 16}}\,{\text{022}}\,{\text{122}}\,{\text{530, }}(5.1 \times {{10}^9})\pi } \right)\) (A1)(ft) (C2)
Note: Follow through from part (b).
[2 marks]
Question
Chocolates in the shape of spheres are sold in boxes of 20.
Each chocolate has a radius of 1 cm.
Find the volume of 1 chocolate.
Write down the volume of 20 chocolates.
The diagram shows the chocolate box from above. The 20 chocolates fit perfectly in the box with each chocolate touching the ones around it or the sides of the box.
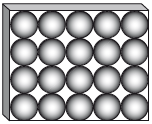
Calculate the volume of the box.
The diagram shows the chocolate box from above. The 20 chocolates fit perfectly in the box with each chocolate touching the ones around it or the sides of the box.

Calculate the volume of empty space in the box.
Answer/Explanation
Markscheme
The first time a correct answer has incorrect or missing units, the final (A1) is not awarded.
\(\frac{4}{3}\pi {(1)^3}\) (M1)
Notes: Award (M1) for correct substitution into correct formula.
\( = 4.19{\text{ }}\left( {{\text{4.18879}} \ldots ,{\text{ }}\frac{4}{3}\pi } \right){\text{ c}}{{\text{m}}^3}\) (A1) (C2)
[2 marks]
The first time a correct answer has incorrect or missing units, the final (A1) is not awarded.
\(83.8{\text{ }}\left( {{\text{83.7758}} \ldots ,{\text{ }}\frac{{80}}{3}\pi } \right){\text{ c}}{{\text{m}}^3}\) (A1)(ft) (C1)
Note: Follow through from their answer to part (a).
[1 mark]
The first time a correct answer has incorrect or missing units, the final (A1) is not awarded.
\(10 \times 8 \times 2\) (M1)
Note: Award (M1) for correct substitution into correct formula.
\( = 160{\text{ c}}{{\text{m}}^3}\) (A1) (C2)
[2 marks]
The first time a correct answer has incorrect or missing units, the final (A1) is not awarded.
\(76.2{\text{ }}\left( {{\text{76.2241}} \ldots ,{\text{ }}\left( {160 – \frac{{80}}{3}\pi } \right)} \right){\text{ c}}{{\text{m}}^3}\) (A1)(ft) (C1)
Note: Follow through from their part (b) and their part (c).
[1 mark]
Question
\(T = \frac{{\left( {\tan (2z) + 1} \right)\left( {2\cos (z) – 1} \right)}}{{{y^2} – {x^2}}}\), where \(x = 9\), \(y = 41\) and \(z = 30^\circ \).
Calculate the exact value of \(T\).
Give your answer to \(T\) correct to
(i) two significant figures;
(ii) three decimal places.
Pyotr estimates the value of \(T\) to be \(0.002\).
Calculate the percentage error in Pyotr’s estimate.
Answer/Explanation
Markscheme
\(\frac{{\left( {\tan (2 \times 30) + 1} \right)\left( {2\cos (30) – 1} \right)}}{{{{41}^2} – {9^2}}}\) (M1)
Note: Award (M1) for correct substitution into formula.
\( = 0.00125\;\;\;\left( {\frac{1}{{800}}} \right)\) (A1) (C2)
Note: Using radians the answer is \( – 0.000570502\), award at most (M1)(A0).
(i) \(0.0013\) (A1)(ft)
Note: Follow through from part (a).
(ii) \(0.001\) (A1)(ft) (C2)
Note: Follow through from part (a).
\(\left| {\frac{{0.002 – 0.00125}}{{0.00125}}} \right| \times 100\) (M1)
Notes: Award (M1) for their correct substitution into the percentage error formula. Absolute value signs are not required.
Their unrounded answer from part (a) must be used.
Do not accept use of answers from part (b).
\( = 60{\text{ (%)}}\) (A1)(ft) (C2)
Notes: The \({\text{%}}\) sign is not required.
The answer from radians is \(450.568{\text{%}}\), award (M1)(A1)(ft).
Follow through from part (a).
Question
Assume the Earth is a perfect sphere with radius 6371 km.
Calculate the volume of the Earth in \({\text{k}}{{\text{m}}^3}\). Give your answer in the form \(a \times {10^k}\), where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\).
The volume of the Moon is \(2.1958 \times {10^{10}}\;{\text{k}}{{\text{m}}^3}\).
Calculate how many times greater in volume the Earth is compared to the Moon.
Give your answer correct to the nearest integer.
Answer/Explanation
Markscheme
\(\frac{4}{3}\pi {(6371)^3}\) (M1)
Note: Award (M1) for correct substitution into volume formula.
\( = 1.08 \times {10^{12}}\;\;\;(1.08320 \ldots \times {10^{12}})\) (A2) (C3)
Notes: Award (A1)(A0) for correct mantissa between 1 and 10, with incorrect index.
Award (A1)(A0) for \(1.08\rm{E}12\)
Award (A0)(A0) for answers of the type: \(108 \times {10^{10}}\).
\(\frac{{1.08320 \ldots \times {{10}^{12}}}}{{2.1958 \times {{10}^{10}}}}\) (M1)
Note: Award (M1) for dividing their answer to part (a) by \(2.1958 \times {10^{10}}\).
\( = 49.3308 \ldots \) (A1)(ft)
Note: Accept \(49.1848…\) from use of 3 sf answer to part (a).
\( = 49\) (A1) (C3)
Notes: Follow through from part (a).
The final (A1) is awarded for their unrounded non-integer answer seen and given correct to the nearest integer.
Do not award the final (A1) for a rounded answer of 0 or if it is incorrect by a large order of magnitude.
