Question
The following diagram shows a perfume bottle made up of a cylinder and a cone.
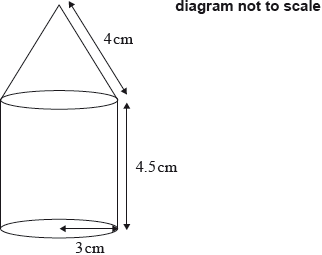
The radius of both the cylinder and the base of the cone is 3 cm.
The height of the cylinder is 4.5 cm.
The slant height of the cone is 4 cm.
(i) Show that the vertical height of the cone is \(2.65\) cm correct to three significant figures.
(ii) Calculate the volume of the perfume bottle.[6]
The bottle contains \({\text{125 c}}{{\text{m}}^{\text{3}}}\) of perfume. The bottle is not full and all of the perfume is in the cylinder part.
Find the height of the perfume in the bottle.[2]
Temi makes some crafts with perfume bottles, like the one above, once they are empty. Temi wants to know the surface area of one perfume bottle.
Find the total surface area of the perfume bottle.[4]
Temi covers the perfume bottles with a paint that costs 3 South African rand (ZAR) per millilitre. One millilitre of this paint covers an area of \({\text{7 c}}{{\text{m}}^{\text{2}}}\).
Calculate the cost, in ZAR, of painting the perfume bottle. Give your answer correct to two decimal places.[4]
Temi sells her perfume bottles in a craft fair for 325 ZAR each. Dominique from France buys one and wants to know how much she has spent, in euros (EUR). The exchange rate is 1 EUR = 13.03 ZAR.
Find the price, in EUR, that Dominique paid for the perfume bottle. Give your answer correct to two decimal places.[2]
Answer/Explanation
Markscheme
(i) \({x^2} + {3^2} = {4^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
Accept correct alternative method using trigonometric ratios.
\(x = 2.64575 \ldots \) (A1)
\(x = 2.65{\text{ }}({\text{cm}})\) (AG)
Note: The unrounded and rounded answer must be seen for the (A1) to be awarded.
OR
\(\sqrt {{4^2} – {3^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
\( = \sqrt 7 \) (A1)
\( = 2.65{\text{ (cm)}}\) (AG)
Note: The exact answer must be seen for the final (A1) to be awarded.
(ii) \(\pi \times {3^2} \times 4.5 + \frac{1}{3}\pi \times {3^2} \times 2.65\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula, (M1) for correct substitution into the volume of a cone formula, (M1) for adding both of their volumes.
\( = 152{\text{ c}}{{\text{m}}^3}\;\;\;(152.210 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}48.45\pi {\text{ c}}{{\text{m}}^3})\) (A1)(G3)
\(\pi {3^2}h = 125\) (M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula.
Accept alternative methods. Accept \(4.43\) (\(4.42913 \ldots \)) from using rounded answers in \(h = \frac{{125 \times 4.5}}{{127}}\).
\(h = 4.42{\text{ (cm)}}\;\;\;\left( {4.42097 \ldots {\text{ (cm)}}} \right)\) (A1)(G2)
\(2\pi \times 3 \times 4.5 + \pi \times 3 \times 4 + \pi \times {3^2}\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into curved surface area of a cylinder formula, (M1) for correct substitution into the curved surface area of a cone formula, (M1) for adding the area of the base of the cylinder to the other two areas.
\( = 151{\text{ c}}{{\text{m}}^2}\;\;\;(150.796 \ldots {\text{ c}}{{\text{m}}^2},{\text{ }}48\pi {\text{ c}}{{\text{m}}^2})\) (A1)(G3)
\(\frac{{150.796 \ldots }}{7} \times 3\) (M1)(M1)
Notes: Award (M1) for dividing their answer to (c) by \(7\), (M1) for multiplying by \(3\). Accept equivalent methods.
\( = 64.63{\text{ (ZAR)}}\) (A1)(ft)(G2)
Notes: The (A1) is awarded for their correct answer, correctly rounded to 2 decimal places. Follow through from their answer to part (c). If rounded answer to part (c) is used the answer is \(64.71\) (ZAR).
\(\frac{{325}}{{13.03}}\) (M1)
Note: Award (M1) for dividing \(325\) by \(13.03\).
\( = 24.94{\text{ (EUR)}}\) (A1)(G2)
Note: The (A1) is awarded for the correct answer rounded to 2 decimal places, unless already penalized in part (d).
Question
Nadia designs a wastepaper bin made in the shape of an open cylinder with a volume of \(8000{\text{ c}}{{\text{m}}^3}\).
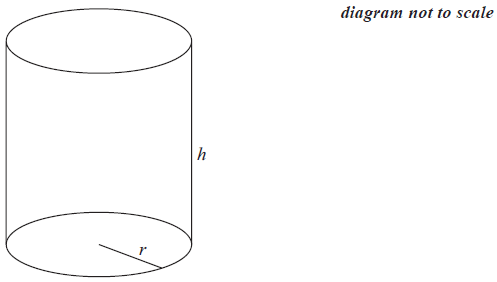
Nadia decides to make the radius, \(r\) , of the bin \(5{\text{ cm}}\).
Merryn also designs a cylindrical wastepaper bin with a volume of \(8000{\text{ c}}{{\text{m}}^3}\). She decides to fix the radius of its base so that the total external surface area of the bin is minimized.
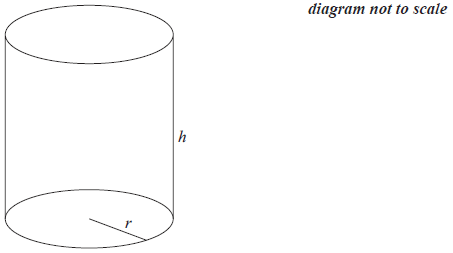
Let the radius of the base of Merryn’s wastepaper bin be \(r\) , and let its height be \(h\) .
Calculate
(i) the area of the base of the wastepaper bin;
(ii) the height, \(h\) , of Nadia’s wastepaper bin;
(iii) the total external surface area of the wastepaper bin.[7]
State whether Nadia’s design is practical. Give a reason.[2]
Write down an equation in \(h\) and \(r\) , using the given volume of the bin.[1]
Show that the total external surface area, \(A\) , of the bin is \(A = \pi {r^2} + \frac{{16000}}{r}\) .[2]
Write down \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\).[3]
(i) Find the value of \(r\) that minimizes the total external surface area of the wastepaper bin.
(ii) Calculate the value of \(h\) corresponding to this value of \(r\) .[5]
Determine whether Merryn’s design is an improvement upon Nadia’s. Give a reason.[2]
Answer/Explanation
Markscheme
(i) \({\text{Area}} = \pi {(5)^2}\) (M1)
\( = 78.5{\text{ (c}}{{\text{m}}^2}{\text{)}}\) (\(78.5398 \ldots \)) (A1)(G2)
Note: Accept \(25\pi \) .
(ii) \(8000 = 78.5398 \ldots \times h\) (M1)
\(h = 102{\text{ (cm)}}\) (\(101.859 \ldots \)) (A1)(ft)(G2)
Note: Follow through from their answer to part (a)(i).
(iii) \({\text{Area}} = \pi {(5)^2} + 2\pi (5)(101.859 \ldots )\) (M1)(M1)
Note: Award (M1) for their substitution in curved surface area formula, (M1) for addition of their two areas.
\( = 3280{\text{ (c}}{{\text{m}}^2}{\text{)}}\) (\(3278.53 \ldots \)) (A1)(ft)(G2)
Note: Follow through from their answers to parts (a)(i) and (ii).
No, it is too tall/narrow. (A1)(ft)(R1)
Note: Follow through from their value for \(h\).
\(8000 = \pi {r^2}h\) (A1)
\(A = \pi {r^2} + 2\pi r\left( {\frac{{8000}}{{\pi {r^2}}}} \right)\) (A1)(M1)
Note: Award (A1) for correct rearrangement of their part (c), (M1) for substitution of their rearrangement into area formula.
\( = \pi {r^2} + \frac{{16000}}{r}\) (AG)
\(\frac{{{\text{d}}A}}{{{\text{d}}r}} = 2\pi r – 16000{r^{ – 2}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi r\) , (A1) for \( – 16000\) (A1) for \({r^{ – 2}}\) . If an extra term is present award at most (A1)(A1)(A0).
(i) \(\frac{{{\text{d}}A}}{{{\text{d}}r}} = 0\) (M1)
\(2\pi {r^3} – 16000 = 0\) (M1)
\(r = 13.7{\text{ cm}}\) (\(13.6556 \ldots \)) (A1)(ft)
Note: Follow through from their part (e).
(ii) \(h = \frac{{8000}}{{\pi {{(13.65 \ldots )}^2}}}\) (M1)
\( = 13.7{\text{ cm}}\) (\(13.6556 \ldots \)) (A1)(ft)
Note: Accept \(13.6\) if \(13.7\) used.
Yes or No, accompanied by a consistent and sensible reason. (A1)(R1)
Note: Award (A0)(R0) if no reason is given.
