Download IITian Academy App for accessing Online Mock Tests and More..
Question
Consider the universal set \(U = \{ x \in \mathbb{N}|3 < x < 13\} \), and the subsets \(A = \{ {\text{multiples of 3}}\} \) and \(B = \{ 4,{\text{ }}6,{\text{ }}12\} \).
List the elements of the following set.
A
List the elements of the following set.
\(A \cap B’\)
Write down one element of \((A \cup B)’\).
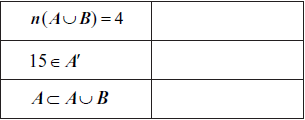
One of the statements in the table below is false. Indicate with an X which statement is false. Give a reason for your answer.
Answer/Explanation
Markscheme
6, 9, 12 (A1) (C1)
[1 mark]
9 (A1)(ft) (C1)
Note: Follow through from their part (a)(i).
[1 mark]
any element from {5, 7, 8, 10, 11} (A1)(A1)(ft) (C2)
Note: Award (A1)(ft) for finding \((A \cup B)\), follow through from their A.
Award full marks if all correct elements of \((A \cup B)’\) are listed.
[2 marks]
\(15 \notin U\) (R1)(A1) (C2)
Notes: Accept correct reason in words.
If the reason is incorrect, both marks are lost.
Do not award (R0)(A1).
[2 marks]
Question
\(U\) is the set of positive integers less than or equal to \(10\).
\(A\), \(B\) and \(C\) are subsets of \(U\).
\(A = \left\{ {{\text{even integers}}} \right\}\)
\(B = \left\{ {{\text{multiples of }}3} \right\}\)
\(C = \left\{ {6,{\text{ }}7,{\text{ }}8,{\text{ }}9} \right\}\)
List the elements of \(A\).
List the elements of \(B\).
Complete the Venn diagram with all the elements of \(U\).
Answer/Explanation
Markscheme
\(2, 4, 6, 8, 10\) (A1) (C1)
Note: Do not penalize the use of \(\left\{ {{\text{ }}} \right\}\).
[1 mark]
\(3, 6, 9\) (A1) (C1)
Note: Do not penalize the use of \(\left\{ {{\text{ }}} \right\}\).
Follow through from part (a) only if their \({\text{U}}\) is listed.
[1 mark]
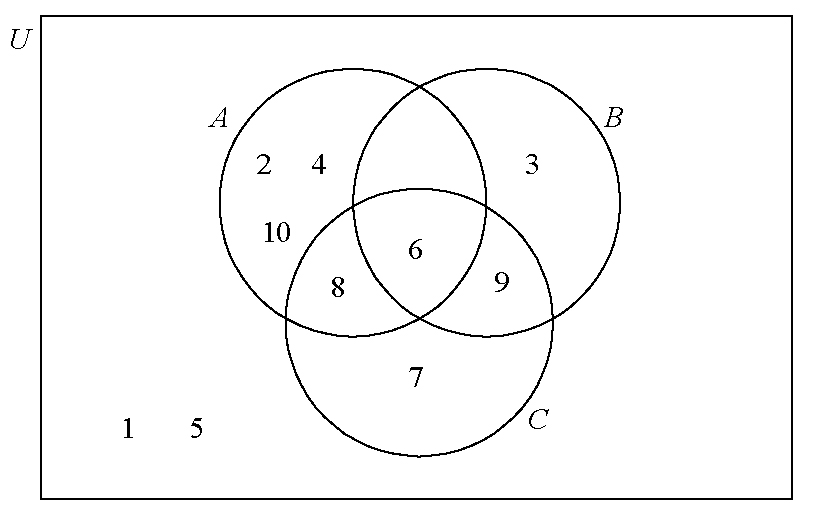(A1)(ft)(A1)(ft)(A1)(ft)(A1)(ft) (C4)
Notes: Award (A1)(ft) for the correct placement of \(6\).
Award (A1)(ft) for the correct placement of \(8\) and \(9\) and the empty region.
Award (A1)(ft) for the correct placement of \(2\), \(4\), \(3\), \(7\), and \(10\).
Award (A1)(ft) for the correct placement of \(1\) and \(5\).
If an element is in more than one region, award (A0) for that element.
Follow through from their answers to parts (a) and (b).
[4 marks]