Question
Jenny has a circular cylinder with a lid. The cylinder has height 39 cm and diameter 65 mm.
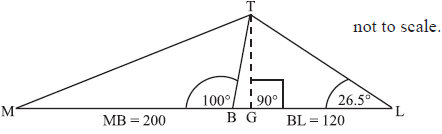
An old tower (BT) leans at 10° away from the vertical (represented by line TG).
The base of the tower is at B so that \({\text{M}}\hat {\rm B}{\text{T}} = 100^\circ \).
Leonardo stands at L on flat ground 120 m away from B in the direction of the lean.
He measures the angle between the ground and the top of the tower T to be \({\text{B}}\hat {\rm L}{\text{T}} = 26.5^\circ \).
Calculate the volume of the cylinder in cm3. Give your answer correct to two decimal places.[3]
The cylinder is used for storing tennis balls. Each ball has a radius of 3.25 cm.
Calculate how many balls Jenny can fit in the cylinder if it is filled to the top.[1]
(i) Jenny fills the cylinder with the number of balls found in part (b) and puts the lid on. Calculate the volume of air inside the cylinder in the spaces between the tennis balls.
(ii) Convert your answer to (c) (i) into cubic metres.[4]
(i) Find the value of angle \({\text{B}}\hat {\rm T}{\text{L}}\).
(ii) Use triangle BTL to calculate the sloping distance BT from the base, B to the top, T of the tower.[5]
Calculate the vertical height TG of the top of the tower.[2]
Leonardo now walks to point M, a distance 200 m from B on the opposite side of the tower. Calculate the distance from M to the top of the tower at T.[3]
Answer/Explanation
Markscheme
\(\pi \times 3.25^2 \times 39\) (M1)(A1)
(= 1294.1398)
Answer 1294.14 (cm3)(2dp) (A1)(ft)(G2)
(UP) not applicable in this part due to wording of question. (M1) is for substituting appropriate numbers from the problem into the correct formula, even if the units are mixed up. (A1) is for correct substitutions or correct answer with more than 2dp in cubic centimetres seen. Award (G1) for answer to > 2dp with no working and no attempt to correct to 2dp. Award (M1)(A0)(A1)(ft) for \(\pi \times {32.5^2} \times 39{\text{ c}}{{\text{m}}^3}\) (= 129413.9824) = 129413.98
Use of \(\pi = \frac{22}{7}\) or 3.142 etc is premature rounding and is awarded at most (M1)(A1)(A0) or (M1)(A0)(A1)(ft) depending on whether the intermediate value is seen or not. For all other incorrect substitutions, award (M1)(A0) and only follow through the 2 dp correction if the intermediate answer to more decimal places is seen. Answer given as a multiple of \(\pi\) is awarded at most (M1)(A1)(A0). As usual, an unsubstituted formula followed by correct answer only receives the G marks.[3 marks]
39/6.5 = 6 (A1)[1 mark]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) (i) Volume of one ball is \(\frac{4}{3} \pi \times 3.25^3 {\text{ cm}}^3\) (M1)
\({\text{Volume of air}} = \pi \times {3.25^2} \times 39 – 6 \times \frac{4}{3}\pi \times {3.25^3} = 431{\text{ c}}{{\text{m}}^3}\) (M1)(A1)(ft)(G2)
Award first (M1) for substituted volume of sphere formula or for numerical value of sphere volume seen (143.79… or 45.77… \( \times \pi\)). Award second (M1) for subtracting candidate’s sphere volume multiplied by their answer to (b). Follow through from parts (a) and (b) only, but negative or zero answer is always awarded (A0)(ft)
(UP) (ii) 0.000431m3 or 4.31×10−4 m3 (A1)(ft)[4 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) \({\text{Angle B}}\widehat {\text{T}}{\text{L}} = 180 – 80 – 26.5\) or \(180 – 90 – 26.5 – 10\) (M1)
\(= 73.5^\circ\) (A1)(G2)
(ii) \(\frac{{BT}}{{\sin (26.5^\circ )}} = \frac{{120}}{{\sin (73.5^\circ )}}\) (M1)(A1)(ft)
(UP) BT = 55.8 m (3sf) (A1)(ft)[5 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Unit penalty (UP) is applicable where indicated in the left hand column.
TG = 55.8sin(80°) or 55.8cos(10°) (M1)
(UP) = 55.0 m (3sf) (A1)(ft)(G2)
Apply (AP) if 0 missing[2 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Unit penalty (UP) is applicable where indicated in the left hand column.
\({\text{MT}}^2 = 200^2 + 55.8^2 – 2 \times 200 \times 55.8 \times \cos(100^\circ)\) (M1)(A1)(ft)
(UP) MT = 217 m (3sf) (A1)(ft)
Follow through only from part (ii)(a)(ii). Award marks at discretion for any valid alternative method.[3 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Question
The natural numbers: 1, 2, 3, 4, 5… form an arithmetic sequence.
A geometric progression \(G_1\) has 1 as its first term and 3 as its common ratio.
State the values of u1 and d for this sequence.[2]
Use an appropriate formula to show that the sum of the natural numbers from 1 to n is given by \(\frac{1}{2}n (n +1)\).[2]
Calculate the sum of the natural numbers from 1 to 200.[2]
The sum of the first n terms of G1 is 29 524. Find n.[3]
A second geometric progression G2 has the form \(1,\frac{1}{3},\frac{1}{9},\frac{1}{{27}}…\)[1]
Calculate the sum of the first 10 terms of G2.[2]
Explain why the sum of the first 1000 terms of G2 will give the same answer as the sum of the first 10 terms, when corrected to three significant figures.[1]
Using your results from parts (a) to (c), or otherwise, calculate the sum of the first 10 terms of the sequence \(2,3\frac{1}{3},9\frac{1}{9},27\frac{1}{{27}}…\)
Give your answer correct to one decimal place.[3]
Answer/Explanation
Markscheme
\(u_1 = d = 1\). (A1)(A1)[2 marks]
Sum is \(\frac{1}{2}n(2{u_1} + d(n – 1))\) or \(\frac{1}{2}n({u_1} + {u_n})\) (M1)
Award (M1) for either sum formula seen, even without substitution.
So sum is \(\frac{1}{2}n(2 + (n – 1)) = \frac{1}{2}n(n + 1)\) (A1)(AG)
Award (A1) for substitution of \({u_1} = 1 = d\) or \({u_1} = 1\) and \({u_n} = n\) with simplification where appropriate. \(\frac{1}{2}n(n + 1)\) must be seen to award this (A1).[2 marks]
\(\frac{1}{2}(200)(201) = 20 100\) (M1)(A1)(G2)
(M1) is for correct formula with correct numerical input. Original sum formula with u, d and n can be used.[2 marks]
\(\frac{{1 – {3^n}}}{{1 – 3}} = 29524\) (M1)(A1)
(M1) for correctly substituted formula on one side, (A1) for = 29524 on the other side.
n = 10. (A1)(G2)
Trial and error is a valid method. Award (M1) for at least \(\frac{{1 – {3^{10}}}}{{1 – 3}}\) seen and then (A1) for = 29524, (A1) for \(n = 10\). For only unproductive trials with \(n \ne 10\), award (M1) and then (A1) if the evaluation is correct.[3 marks]
Common ratio is \(\frac{1}{3}\), (0.333 (3sf) or 0.3) (A1)
Accept ‘divide by 3’.[1 mark]
\(\frac{{1 – {{\left( {\frac{1}{3}} \right)}^{10}}}}{{1 – \frac{1}{3}}}\) (M1)
= 1.50 (3sf) (A1)(ft)(G1)
1.5 and \(\frac{3}{2}\) receive (A0)(AP) if AP not yet used Incorrect formula seen in (a) or incorrect value in (b) can follow through to (c). Can award (M1) for \(1 + \left( {\frac{1}{3}} \right) + \left( {\frac{1}{9}} \right) + ……\)[2 marks]
Both \({\left( {\frac{1}{3}} \right)^{10}}\) and \({\left( {\frac{1}{3}} \right)^{1000}}\) (or those numbers divided by 2/3) are 0 when corrected to 3sf, so they make no difference to the final answer. (R1)
Accept any valid explanation but please note: statements which only convey the idea of convergence are not enough for (R1). The reason must show recognition that the convergence is adequately fast (though this might be expressed in a much less technical manner).[1 mark]
The sequence given is \(G_1 + G_2\) (M1)
The sum is 29 524 + 1.50 (A1)(ft)
= 29 525.5 (A1)(ft)(G2)
The (M1) is implied if the sum of the two numbers is seen. Award (G1) for 29 500 with no working. (M1) can be awarded for
\(2 + 3\frac{1}{3} + …\) Award final (A1) only for answer given correct to 1dp.[3 marks]
Question
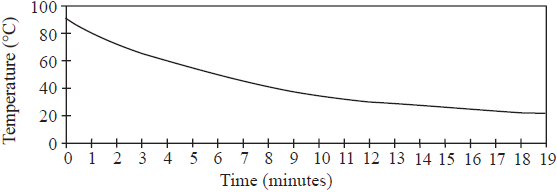
The following graph shows the temperature in degrees Celsius of Robert’s cup of coffee, \(t\) minutes after pouring it out. The equation of the cooling graph is \(f (t) = 16 + 74 \times 2.8^{−0.2t}\) where \(f (t)\) is the temperature and \(t\) is the time in minutes after pouring the coffee out.
Robert, who lives in the UK, travels to Belgium. The exchange rate is 1.37 euros to one British Pound (GBP) with a commission of 3 GBP, which is subtracted before the exchange takes place. Robert gives the bank 120 GBP.
Find the initial temperature of the coffee.[1]
Write down the equation of the horizontal asymptote.[1]
Find the room temperature.[1]
Find the temperature of the coffee after 10 minutes.[1]
Find the temperature of Robert’s coffee after being heated in the microwave for 30 seconds after it has reached the temperature in part (d).[3]
Calculate the length of time it would take a similar cup of coffee, initially at 20°C, to be heated in the microwave to reach 100°C.[4]
Calculate correct to 2 decimal places the amount of euros he receives.[3]
He buys 1 kilogram of Belgian chocolates at 1.35 euros per 100 g.
Calculate the cost of his chocolates in GBP correct to 2 decimal places.[3]
Answer/Explanation
Markscheme
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
(UP) 90°C (A1)[1 mark]
y = 16 (A1)[1 mark]
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
(UP) 16°C (ft) from answer to part (b) (A1)(ft)[1 mark]
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
(UP) 25.4°C (A1)[1 mark]
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
for seeing 20.75 or equivalent (A1)
for multiplying their (d) by their 20.75 (M1)
(UP) 42.8°C (A1)(ft)(G2)[3 marks]
Unit penalty (UP) is applicable in part (i)(a)(c)(d)(e) and (f)
for seeing \(20 \times 2^{1.5t} = 100\) (A1)
for seeing a value of t between 1.54 and 1.56 inclusive (M1)(A1)
(UP) 1.55 minutes or 92.9 seconds (A1)(G3)[4 marks]
Financial accuracy penalty (FP) is applicable in part (ii) only.
\(120 – 3 = 117\)
(FP) \(117 \times 1.37\) (A1)
= 160.29 euros (correct answer only) (M1)
first (A1) for 117 seen, (M1) for multiplying by 1.37 (A1)(G2)
[3 marks]
Financial accuracy penalty (FP) is applicable in part (ii) only.
(FP) \(\frac{{13.5}}{{1.37}}\) (A1)(M1)
9.85 GBP (answer correct to 2dp only)
first (A1) is for 13.5 seen, (M1) for dividing by 1.37 (A1)(ft)(G3)[3 marks]
Question
A random sample of 167 people who own mobile phones was used to collect data on the amount of time they spent per day using their phones. The results are displayed in the table below.
Manuel conducts a survey on a random sample of 751 people to see which television programme type they watch most from the following: Drama, Comedy, Film, News. The results are as follows.
Manuel decides to ignore the ages and to test at the 5 % level of significance whether the most watched programme type is independent of gender.
State the modal group.[1]
Use your graphic display calculator to calculate approximate values of the mean and standard deviation of the time spent per day on these mobile phones.[3]
On graph paper, draw a fully labelled histogram to represent the data.[4]
Draw a table with 2 rows and 4 columns of data so that Manuel can perform a chi-squared test.[3]
State Manuel’s null hypothesis and alternative hypothesis.[1]
Find the expected frequency for the number of females who had ‘Comedy’ as their most-watched programme type. Give your answer to the nearest whole number.[2]
Using your graphic display calculator, or otherwise, find the chi-squared statistic for Manuel’s data.[3]
(i) State the number of degrees of freedom available for this calculation.
(ii) State his conclusion.[3]
Answer/Explanation
Markscheme
\(45 \leqslant t < 60\) (A1)[1 mark]
Unit penalty (UP) is applicable in question part (i)(b) only.
(UP) 42.4 minutes (G2)
21.6 minutes (G1)[3 marks]
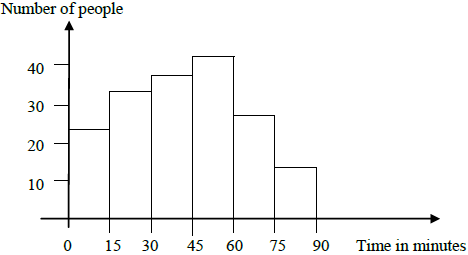(A4)[4 marks]
(M1)(M1)(A1)[3 marks]
H0: favourite TV programme is independent of gender or no association between favourite TV programme and gender
H1: favourite TV programme is dependent on gender (must have both) (A1)[1 mark]
\(\frac{{365 \times 217}}{{751}}\) (M1)
\(= 105\) (A1)(ft)(G2)[2 marks]
12.6 (accept 12.558) (G3)[3 marks]
(i) 3 (A1)
(ii) reject H0 or equivalent statement (e.g. accept H1) (A1)(ft)[3 marks]
Question
Consider the functions \(f(x) = \frac{{2x + 3}}{{x + 4}}\) and \(g(x) = x + 0.5\) .
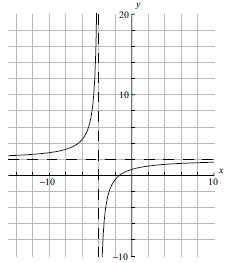
Sketch the graph of the function \(f(x)\), for \( – 10 \leqslant x \leqslant 10\) . Indicating clearly the axis intercepts and any asymptotes.[6]
Write down the equation of the vertical asymptote.[2]
On the same diagram as part (a) sketch the graph of \(g(x) = x + 0.5\) .[2]
Using your graphical display calculator write down the coordinates of one of the points of intersection on the graphs of \(f\) and \(g\), giving your answer correct to five decimal places.[3]
Write down the gradient of the line \(g(x) = x + 0.5\) .[1]
The line \(L\) passes through the point with coordinates \(( – 2{\text{, }} – 3)\) and is perpendicular to the line \(g(x)\) . Find the equation of \(L\).[3]
Answer/Explanation
Markscheme
(A6)
Notes: (A1) for labels and some idea of scale.
(A1) for \(x\)-intercept seen, (A1) for \(y\)-intercept seen in roughly the correct places (coordinates not required).
(A1) for vertical asymptote seen, (A1) for horizontal asymptote seen in roughly the correct places (equations of the lines not required).
(A1) for correct general shape.[6 marks]
\(x = – 4\) (A1)(A1)(ft)
Note: (A1) for \(x =\), (A1)(ft) for \( – 4\).[2 marks]
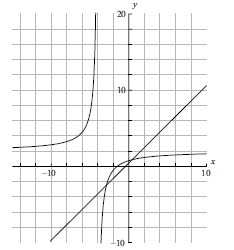(A1)(A1)
Note: (A1) for correct axis intercepts, (A1) for straight line[2 marks]
\(( – 2.85078{\text{, }} – 2.35078)\) OR \((0.35078{\text{, }}0.85078)\) (G1)(G1)(A1)(ft)
Notes: (A1) for \(x\)-coordinate, (A1) for \(y\)-coordinate, (A1)(ft) for correct accuracy. Brackets required. If brackets not used award (G1)(G0)(A1)(ft).
Accept \(x = – 2.85078\), \(y = – 2.35078\) or \(x = 0.35078\), \(y = 0.85078\).[3 marks]
\({\text{gradient}} = 1\) (A1)[1 mark]
\({\text{gradient of perpendicular}} = – 1\) (A1)(ft)
(can be implied in the next step)
\(y = mx + c\)
\( – 3 = – 1 \times – 2 + c\) (M1)
\(c = – 5\)
\(y = – x – 5\) (A1)(ft)(G2)
OR
\(y + 3 = – (x + 2)\) (M1)(A1)(ft)(G2)
Note: Award (G2) for correct answer with no working at all but (A1)(G1) if the gradient is mentioned as \( – 1\) then correct answer with no further working.[3 marks]
Question
Alex and Kris are riding their bicycles together along a bicycle trail and note the following distance markers at the given times.
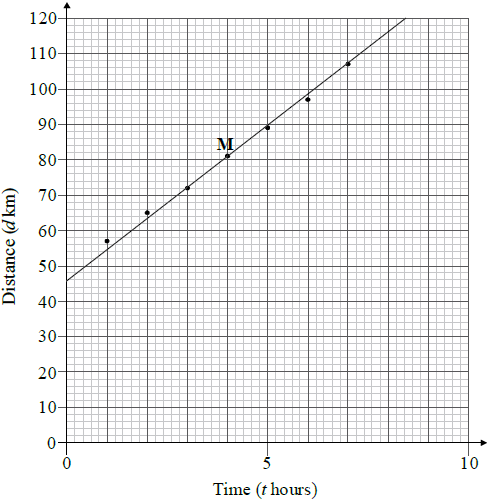
Draw a scatter diagram of the data. Use 1 cm to represent 1 hour and 1 cm to represent 10 km.[3]
Write down for this set of data the mean time, \(\bar t\).[1]
Write down for this set of data the mean distance, \(\bar d\).[1]
Mark and label the point \(M(\bar t,{\text{ }}\bar d)\) on your scatter diagram.[2]
Draw the line of best fit on your scatter diagram.[2]
Using your graph, estimate the time when Alex and Kris pass the 85 km distance marker. Give your answer correct to one decimal place.[2]
Write down the equation of the regression line for the data given.[2]
Using your equation calculate the distance marker passed by the cyclists at 10.3 hours.[2]
Is this estimate of the distance reliable? Give a reason for your answer.[2]
Answer/Explanation
Markscheme
(A1)(A2)
Notes: Award (A1) for axes labelled with d and t and correct scale, (A2) for 6 or 7 points correctly plotted, (A1) for 4 or 5 points, (A0) for 3 or less points correctly plotted. Award at most (A1)(A1) if points are joined up. If axes are reversed award at most (A0)(A2)[3 marks]
\(\bar t = 4\) (G1)[1 mark]
\(\bar d = 81.1\left( {\frac{{568}}{7}} \right)\) (G1)
Note: If answers are the wrong way around award in (i) (G0) and in (ii) (G1)(ft).[1 mark]
Point marked and labelled with M or \(\bar t\), \(\bar d\) on their graph (A1)(ft)(A1)(ft)[2 marks]
Line of best fit drawn that passes through their M and (0, 48) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for straight line that passes through their M, (A1) for line (extrapolated if necessary) that passes through (0, 48).
Accept error of ±3. If ruler not used award a maximum of (A1)(ft)(A0).[2 marks]
4.5h (their answer ±0.2) (M1)(A1)(ft)(G2)
Note: Follow through from their graph. If method shown by some indication on graph of point but answer is incorrect, award (M1)(A0).[2 marks]
d = 8.25t + 48.1 (G1)(G1)
Notes: Award (G1) for 8.25, (G1) for 48.1.
Award at most (G1)(G0) if d = (or y =) is not seen.
Accept d – 81.1 = 8.25(t – 4) or equivalent.[2 marks]
d = 8.25 × 10.3 + 48.1 (M1)
d = 133 km (A1)(ft)(G2)[2 marks]
No (A1)
Outside the set of values of t or equivalent. (R1)
Note: Do not award (A1)(R0).[2 marks]
Question
Pauline owns a piece of land ABCD in the shape of a quadrilateral. The length of BC is \(190{\text{ m}}\) , the length of CD is \(120{\text{ m}}\) , the length of AD is \(70{\text{ m}}\) , the size of angle BCD is \({75^ \circ }\) and the size of angle BAD is \({115^ \circ }\) .
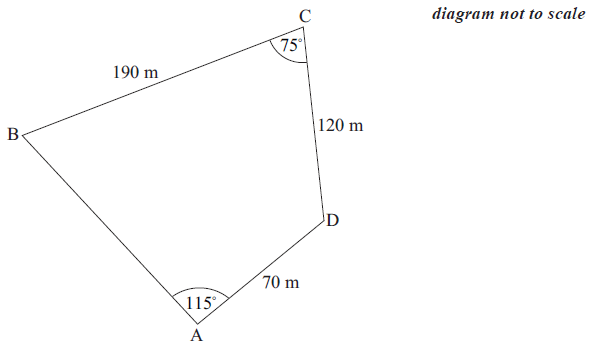
Pauline decides to sell the triangular portion of land ABD . She first builds a straight fence from B to D .
Calculate the length of the fence.[3]
The fence costs \(17\) USD per metre to build.
Calculate the cost of building the fence. Give your answer correct to the nearest USD.[2]
Show that the size of angle ABD is \({18.8^ \circ }\) , correct to three significant figures.[3]
Calculate the area of triangle ABD .[4]
She sells the land for \(120\) USD per square metre.
Calculate the value of the land that Pauline sells. Give your answer correct to the nearest USD.[2]
Pauline invests \(300 000\) USD from the sale of the land in a bank that pays compound interest compounded annually.
Find the interest rate that the bank pays so that the investment will double in value in 15 years.[4]
Answer/Explanation
Markscheme
\({\text{B}}{{\text{D}}^2} = {190^2} + {120^2} – 2(190)(120)\cos {75^ \circ }\) (M1)(A1)
Note: Award (M1) for substituted cosine formula, (A1) for correct substitution.
\(= 197\) m (A1)(G2)
Note: If radians are used award a maximum of (M1)(A1)(A0).[3 marks]
\({\text{cost}} = 196.717 \ldots \times 17\) (M1)
\( = 3344{\text{ USD}}\) (A1)(ft)(G2)
Note: Accept \(3349\) from \(197\).[2 marks]
\(\frac{{\sin ({\text{ABD}})}}{{70}} = \frac{{\sin ({{115}^ \circ })}}{{196.7}}\) (M1)(A1)
Note: Award (M1) for substituted sine formula, (A1) for correct substitution.
\( = {18.81^ \circ } \ldots \) (A1)(ft)
\( = {18.8^ \circ } \) (AG)
Notes: Both the unrounded and rounded answers must be seen for the final (A1) to be awarded. Follow through from their (a). If 197 is used the unrounded answer is \( = {18.78^ \circ } \ldots \)[3 marks]
\({\text{angle BDA}} = {46.2^ \circ }\) (A1)
\({\text{Area}} = \frac{{70 \times (196.717 \ldots ) \times \sin ({{46.2}^ \circ })}}{2}\) (M1)(A1)
Note: Award (M1) for substituted area formula, (A1) for correct substitution.
\({\text{Area ABD}} = 4970{\text{ }}{{\text{m}}^2}\) (A1)(ft)(G2)
Notes: If \(197\) used answer is \(4980\).
Notes: Follow through from (a) only. Award (G2) if there is no working shown and \({46.2^ \circ }\) not seen. If \({46.2^ \circ }\) seen without subsequent working, award (A1)(G2).[4 marks]
\(4969.38 \ldots \times 120\) (M1)
\( = 596 327{\text{ USD}}\) (A1)(ft)(G2)
Notes: Follow through from their (d).[2 marks]
\(300000{\left( {1 + \frac{r}{{100}}} \right)^{15}} = 600000\) or equivalent (A1)(M1)(A1)
Notes: Award (A1) for \(600 000\) seen or implied by alternative formula, (M1) for substituted CI formula, (A1) for correct substitutions.
\(r = 4.73\) (A1)(ft)(G3)
Notes: Award (G3) for \(4.73\) with no working. Award (G2) for \(4.7\) with no working.[4 marks]
Question
A solid metal cylinder has a base radius of 4 cm and a height of 8 cm.
Find the area of the base of the cylinder.[2]
Show that the volume of the metal used in the cylinder is 402 cm3, given correct to three significant figures.[2]
Find the total surface area of the cylinder.[3]
The cylinder was melted and recast into a solid cone, shown in the following diagram. The base radius OB is 6 cm.
Find the height, OC, of the cone.[3]
The cylinder was melted and recast into a solid cone, shown in the following diagram. The base radius OB is 6 cm.
Find the size of angle BCO.[2]
The cylinder was melted and recast into a solid cone, shown in the following diagram. The base radius OB is 6 cm.
Find the slant height, CB.[2]
The cylinder was melted and recast into a solid cone, shown in the following diagram. The base radius OB is 6 cm.
Find the total surface area of the cone.[4]
Answer/Explanation
Markscheme
\( \pi \times 4^2\) (M1)
= 50.3 (16\(\pi\)) cm2 (50.2654…) (A1)(G2)
Note: Award (M1) for correct substitution in area formula. The answer is 50.3 cm2, the units are required.[2 marks]
50.265…× 8 (M1)
Note: Award (M1) for correct substitution in the volume formula.
= 402.123… (A1)
= 402 (cm3) (AG)
Note: Both the unrounded and the rounded answer must be seen for the (A1) to be awarded. The units are not required[2 marks]
\(2 \times \pi \times 4 \times 8 + 2 \times \pi \times 4^2\) (M1)(M1)
Note: Award (M1) for correct substitution in the curved surface area formula, (M1) for adding the area of their two bases.
= 302 cm2 (96π cm2) (301.592…) (A1)(ft)(G2)
Notes: The answer is 302 cm2, the units are required. Do not penalise for missing or incorrect units if penalised in part (a). Follow through from their answer to part (a).[3 marks]
\(\frac{1}{3} \pi \times 6^2 \times \text{OC} = 402\) (M1)(M1)
Note: Award (M1) for correctly substituted volume formula, (M1) for equating to 402 (402.123…).
\({\text{OC}} = 10.7{\text{ (cm)}}\left( {{\text{10}}\frac{2}{3},{\text{ }}10.6666…} \right)\) (A1)(G2)[3 marks]
\(\tan \text{BCO} = \frac{6}{10.66…}\) (M1)
Note: Award (M1) for use of correct tangent ratio.
\({\text{B}}{\operatorname{\hat C}}{\text{O}} = 29.4^\circ \) (29.3577…) (A1)(ft)(G2)
Notes: Accept 29.3° (29.2814…) if 10.7 is used. An acceptable alternative method is to calculate CB first and then angle BCO. Allow follow through from parts (d) and (f). Answers range from 29.2° to 29.5°.[2 marks]
\(\text{CB} = \sqrt{{6^2} + {(10.66…)^2}}\) (M1)
OR
\(\sin 29.35…^\circ = \frac{6}{\text{CB}}\) (M1)
OR
\(\cos 29.35…^\circ = \frac{10.66…}{\text{CB}}\) (M1)
CB = 12.2 (cm) (12.2383…) (A1)(ft)(G2)
Note: Accept 12.3 (12.2674…) if 10.7 (and/or 29.3) used. Follow through from part (d) or part (e) as appropriate.[2 marks]
\(\pi \times 6 \times 12.2383… + \pi \times 6^2\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution in curved surface area formula, (M1) for correct substitution in area of circle formula, (M1) for addition of the two areas.
= 344 cm2 (343.785…) (A1)(ft)(G3)
Note: The answer is 344 cm2, the units are required. Do not penalise for missing or incorrect units if already penalised in either part (a) or (c). Accept 345 cm2 if 12.3 is used and 343 cm2 if 12.2 is used. Follow through from their part (f).[4 marks]
Question
A greenhouse ABCDPQ is constructed on a rectangular concrete base ABCD and is made of glass. Its shape is a right prism, with cross section, ABQ, an isosceles triangle. The length of BC is 50 m, the length of AB is 10 m and the size of angle QBA is 35°.
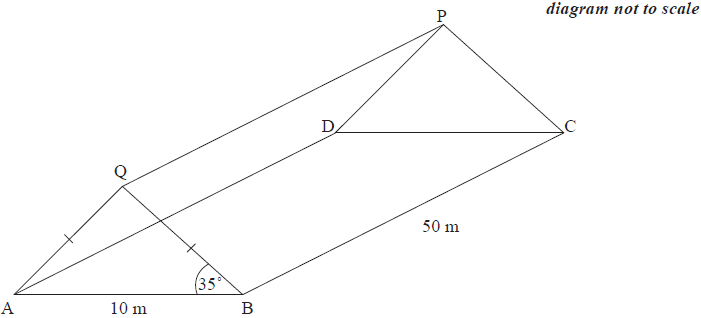
Write down the size of angle AQB.[1]
Calculate the length of AQ.[3]
Calculate the length of AC.[2]
Show that the length of CQ is 50.37 m, correct to 4 significant figures.[2]
Find the size of the angle AQC.[3]
Calculate the total area of the glass needed to construct
(i) the two rectangular faces of the greenhouse;
(ii) the two triangular faces of the greenhouse.[5]
The cost of one square metre of glass used to construct the greenhouse is 4.80 USD.
Calculate the cost of glass to make the greenhouse. Give your answer correct to the nearest 100 USD.[3]
Answer/Explanation
Markscheme
110° (A1)
\(\frac{{AQ}}{{\sin 35^\circ }} = \frac{{10}}{{\sin 110^\circ }}\) (M1)(A1)
Note: Award (M1) for substituted sine rule formula, (A1) for their correct substitutions.
OR
\(AQ = \frac{5}{{\cos 35^\circ }}\) (A1)(M1)
Note: Award (A1) for 5 seen, (M1) for correctly substituted trigonometric ratio.
\(AQ = 6.10\) (6.10387…) (A1)(ft)(G2)
Notes: Follow through from their answer to part (a).
\(AC^2 = 10^2 + 50^2\) (M1)
Note: Award (M1) for correctly substituted Pythagoras formula.
\(AC = 51.0 (\sqrt{2600}, 50.9901…)\) (A1)(G2)
\(QC^2 = (6.10387…)^2 + (50)^2\) (M1)
Note: Award (M1) for correctly substituted Pythagoras formula.
\(QC = 50.3711…\) (A1)
\(= 50.37\) (AG)
Note: Both the unrounded and rounded answers must be seen to award (A1).
If 6.10 is used then 50.3707… is the unrounded answer.
For an incorrect follow through from part (b) award a maximum of (M1)(A0) – the given answer must be reached to award the final (A1)(AG).
\(\cos AQC = \frac{{{{(6.10387…)}^2} + {{(50.3711…)}^2} – {{(50.9901…)}^2}}}{{2(6.10387…)(50.3711…)}}\) (M1)(A1)(ft)
Note: Award (M1) for substituted cosine rule formula, (A1)(ft) for their correct substitutions.
= 92.4° (\({92.3753…^\circ }\)) (A1)(ft)(G2)
Notes: Follow through from their answers to parts (b), (c) and (d). Accept 92.2 if the 3 sf answers to parts (b), (c) and (d) are used.
Accept 92.5° (\({92.4858…^\circ }\)) if the 3 sf answers to parts (b), (c) and 4 sf answers to part (d) used.
(i) \(2(50 \times 6.10387…)\) (M1)
Note: Award (M1) for their correctly substituted rectangular area formula, the area of one rectangle is not sufficient.
= 610 m2 (610.387…) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b).
The answer is 610 m2. The units are required.
(ii) Area of triangular face \( = \frac{1}{2} \times 10 \times 6.10387… \times \sin 35^\circ \) (M1)(A1)(ft)
OR
Area of triangular face \( = \frac{1}{2} \times 6.10387… \times 6.10387… \times \sin 110^\circ \) (M1)(A1)(ft)
\(= 17.5051…\)
Note: Award (M1) for substituted triangle area formula, (A1)(ft) for correct substitutions.
OR
(Height of triangle) \( = {(6.10387…)^2} – {5^2}\)
\(= 3.50103…\)
Area of triangular face \( = \frac{1}{2} \times 10 \times their{\text{ }} height\)
\(= 17.5051…\)
Note: Award (M1) for substituted triangle area formula, (A1)(ft) for correctly substituted area formula. If 6.1 is used, the height is 3.49428… and the area of both triangular faces 34.9 m2
Area of both triangular faces = 35.0 m2 (35.0103…) (A1)(ft)(G2)
Notes: The answer is 35.0 m2. The units are required. Do not penalize if already penalized in part (f)(i). Follow through from their part (b).
(610.387… + 35.0103…) × 4.80 (M1)
= 3097.90… (A1)(ft)
Notes: Follow through from their answers to parts (f)(i) and (f)(ii).
Accept 3096 if the 3 sf answers to part (f) are used.
= 3100 (A1)(ft)(G2)
Notes: Follow through from their unrounded answer, irrespective of whether it is correct. Award (M1)(A2) if working is shown and 3100 seen without the unrounded answer being given.
Question
A cross-country running course consists of a beach section and a forest section. Competitors run from \({\text{A}}\) to \({\text{B}}\), then from \({\text{B}}\) to \({\text{C}}\) and from \({\text{C}}\) back to \({\text{A}}\).
The running course from \({\text{A}}\) to \({\text{B}}\) is along the beach, while the course from \({\text{B}}\), through \({\text{C}}\) and back to \({\text{A}}\), is through the forest.
The course is shown on the following diagram.
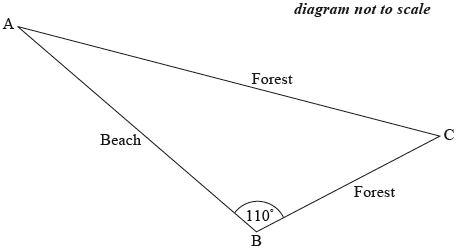
Angle \({\text{ABC}}\) is \(110^\circ\).
It takes Sarah \(5\) minutes and \(20\) seconds to run from \({\text{A}}\) to \({\text{B}}\) at a speed of \(3.8{\text{ m}}{{\text{s}}^{ – 1}}\).
Using ‘distance = speed \( \times \) time’, show that the distance from \({\text{A}}\) to \({\text{B}}\) is \(1220\) metres correct to 3 significant figures.[2]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the speed, in \({\text{m}}{{\text{s}}^{ – 1}}\), that Sarah runs from \({\text{B}}\) to \({\text{C}}\).[1]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the distance, in metres, from \({\mathbf{C}}\) to \({\mathbf{A}}\).[3]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the total distance, in metres, of the cross-country running course.[2]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Find the size of angle \({\text{BCA}}\).[3]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the area of the cross-country course bounded by the lines \({\text{AB}}\), \({\text{BC}}\) and \({\text{CA}}\).[3]
Answer/Explanation
Markscheme
\(3.8 \times 320\) (A1)
Note: Award (A1) for \(320\) or equivalent seen.
\( = 1216\) (A1)
\( = 1220{\text{ (m)}}\) (AG)
Note: Both unrounded and rounded answer must be seen for the final (A1) to be awarded.[2 marks]
\(\frac{{850}}{{303}}{\text{ (m}}{{\text{s}}^{ – 1}}){\text{ (2.81, 2.80528}} \ldots {\text{)}}\) (A1)(G1)[1 mark]
\({\text{A}}{{\text{C}}^2} = {1220^2} + {850^2} – 2(1220)(850)\cos 110^\circ \) (M1)(A1)
Note: Award (M1) for substitution into cosine rule formula, (A1) for correct substitutions.
\({\text{AC}} = 1710{\text{ (m) (1708.87}} \ldots {\text{)}}\) (A1)(G2)
Notes: Accept \(1705{\text{ }} (1705.33…)\).[3 marks]
\(1220 + 850 + {\text{1708.87}} \ldots \) (M1)
\( = {\text{3780 (m) (3778.87}} \ldots {\text{)}}\) (A1)(ft)(G1)
Notes: Award (M1) for adding the three sides. Follow through from their answer to part (c). Accept \(3771{\text{ }} (3771.33…)\).[2 marks]
\(\frac{{\sin C}}{{1220}} = \frac{{\sin 110^\circ }}{{{\text{1708.87}} \ldots }}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into sine rule formula, (A1)(ft) for correct substitutions. Follow through from their part (c).
\(C = 42.1^\circ {\text{ (42.1339}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Accept \(41.9^{\circ}, 42.0^{\circ}, 42.2^{\circ}, 42.3^{\circ}\).
OR
\(\cos C = \frac{{{\text{1708.87}}{ \ldots ^2} + {{850}^2} – {{1220}^2}}}{{2 \times {\text{1708.87}} \ldots \times 850}}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into cosine rule formula, (A1)(ft) for correct substitutions. Follow through from their part (c).
\(C = 42.1^\circ {\text{ (42.1339}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Accept \(41.2^{\circ}, 41.8^{\circ}, 42.4^{\circ}\).[3 marks]
\(\frac{1}{2} \times 1220 \times 850 \times \sin 110^\circ \) (M1)(A1)(ft)
OR
\(\frac{1}{2} \times {\text{1708.87}} \ldots \times 850 \times \sin {\text{42.1339}} \ldots ^\circ \) (M1)(A1)(ft)
OR
\(\frac{1}{2} \times 1220 \times {\text{1708.87}} \ldots \times \sin {\text{27.8661}} \ldots ^\circ \) (M1)(A1)(ft)
Note: Award (M1) for substitution into area formula, (A1)(ft) for correct substitution.
\( = 487\,000{\text{ }}{{\text{m}}^2}{\text{ (487}}\,{\text{230}} \ldots {\text{ }}{{\text{m}}^2})\) (A1)(ft)(G2)
Notes: The answer is \(487\,000{\text{ }}{{\text{m}}^2}\), units are required.
Accept \(486\,000{\text{ }}{{\text{m}}^2}{\text{ (485}}\,{\text{633}} \ldots {\text{ }}{{\text{m}}^2})\).
If workings are not shown and units omitted, award (G1) for \(487\,000{\text{ or }}486\,000\).
Follow through from parts (c) and (e).[3 marks]
Question
A surveyor has to calculate the area of a triangular piece of land, DCE.
The lengths of CE and DE cannot be directly measured because they go through a swamp.
AB, DE, BD and AE are straight paths. Paths AE and DB intersect at point C.
The length of AB is 15 km, BC is 10 km, AC is 12 km, and DC is 9 km.
The following diagram shows the surveyor’s information.
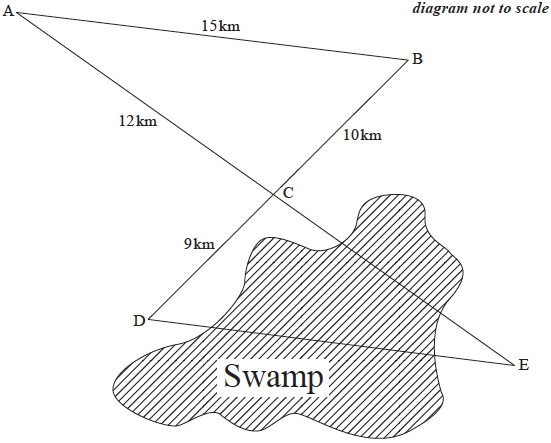
(i) Find the size of angle \({\rm{ACB}}\).
(ii) Show that the size of angle \({\rm{DCE}}\) is \(85.5^\circ\), correct to one decimal place.[4]
The surveyor measures the size of angle \({\text{CDE}}\) to be twice that of angle \({\text{DEC}}\).
(i) Using angle \({\text{DCE}} = 85.5^\circ \), find the size of angle \({\text{DEC}}\).
(ii) Find the length of \({\text{DE}}\).[5]
Calculate the area of triangle \({\text{DEC}}\).[4]
Answer/Explanation
Markscheme
(i) \(\cos {\rm{A\hat CB}} = \frac{{{{10}^2} + {{12}^2} – {{15}^2}}}{{2 \times 10 \times 12}}\) (M1)(A1)
Note: Award (M1) for substituted cosine rule,
(A1) for correct substitution.
\({\rm{A\hat CB}} = 85.5^\circ \;\;\;({\text{85.4593}} \ldots {\text{)}}\) (A1)(G2)
(ii) \({\rm{D\hat CE}} = {\rm{A\hat CB}}\;\;\;{\text{and}}\;\;\;{\rm{A\hat CB}} = 85.5^\circ \;\;\;({\text{85.4593}} \ldots ^\circ {\text{)}}\) (A1)
OR
\({\rm{B\hat CE}} = 180^\circ – 85.5^\circ = 94.5^\circ \;\;\;{\text{and}}\;\;\;{\rm{D\hat CE}} = 180^\circ – 94.5^\circ = 85.5^\circ \) (A1)
Notes: Both reasons must be seen for the (A1) to be awarded.
\({\rm{D\hat CE}} = 85.5^\circ \) (AG)
(i) \({\rm{D\hat EC}} = \frac{{180^\circ – 85.5^\circ }}{3}\) (M1)
\({\rm{D\hat EC}} = 31.5^\circ \) (A1)(G2)
(ii) \(\frac{{\sin (31.5^\circ )}}{9} = \frac{{\sin (85.5^\circ )}}{{{\text{DE}}}}\) (M1)(A1)(ft)
Note: Award (M1) for substituted sine rule, (A1) for correct substitution.
\({\text{DE}} = 17.2{\text{ (km)}}(17.1718 \ldots )\). (A1)(ft)(G2)
\(0.5 \times 17.1718 \ldots \times 9 \times \sin (63^\circ )\) (A1)(ft)(M1)(A1)(ft)
Note: Award (A1)(ft) for \(63\) seen, (M1) for substituted triangle area formula, (A1)(ft) for \(0.5 \times 17.1718 \ldots \times 9 \times \sin ({\text{their angle CDE}})\).
OR
\({\text{(triangle height}} = ){\text{ }}9 \times \sin (63^\circ )\) (A1)(ft)(A1)(ft)
\({\text{0.5}} \times {\text{17.1718}} \ldots \times {\text{9}} \times {\text{sin(their angle CDE)}}\) (M1)
Note: Award (A1)(ft) for \(63\) seen, (A1)(ft) for correct triangle height with their angle \({\text{CDE}}\), (M1) for \({\text{0.5}} \times {\text{17.1718}} \ldots \times {\text{9}} \times {\text{sin(their angle CDE)}}\).
\( = 68.9{\text{ k}}{{\text{m}}^2}\;\;\;(68.8509 \ldots )\) (A1)(ft)(G3)
Notes: Units are required for the last (A1)(ft) mark to be awarded.
Follow through from parts (b)(i) and (b)(ii).
Follow through from their angle \({\text{CDE}}\) within this part of the question.
Question
The following diagram shows a perfume bottle made up of a cylinder and a cone.
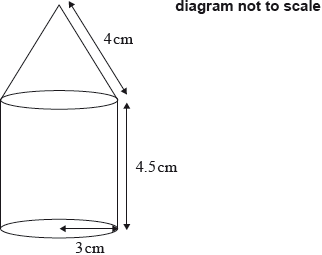
The radius of both the cylinder and the base of the cone is 3 cm.
The height of the cylinder is 4.5 cm.
The slant height of the cone is 4 cm.
(i) Show that the vertical height of the cone is \(2.65\) cm correct to three significant figures.
(ii) Calculate the volume of the perfume bottle.[6]
The bottle contains \({\text{125 c}}{{\text{m}}^{\text{3}}}\) of perfume. The bottle is not full and all of the perfume is in the cylinder part.
Find the height of the perfume in the bottle.[2]
Temi makes some crafts with perfume bottles, like the one above, once they are empty. Temi wants to know the surface area of one perfume bottle.
Find the total surface area of the perfume bottle.[4]
Temi covers the perfume bottles with a paint that costs 3 South African rand (ZAR) per millilitre. One millilitre of this paint covers an area of \({\text{7 c}}{{\text{m}}^{\text{2}}}\).
Calculate the cost, in ZAR, of painting the perfume bottle. Give your answer correct to two decimal places.[4]
Temi sells her perfume bottles in a craft fair for 325 ZAR each. Dominique from France buys one and wants to know how much she has spent, in euros (EUR). The exchange rate is 1 EUR = 13.03 ZAR.
Find the price, in EUR, that Dominique paid for the perfume bottle. Give your answer correct to two decimal places.[2]
Answer/Explanation
Markscheme
(i) \({x^2} + {3^2} = {4^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
Accept correct alternative method using trigonometric ratios.
\(x = 2.64575 \ldots \) (A1)
\(x = 2.65{\text{ }}({\text{cm}})\) (AG)
Note: The unrounded and rounded answer must be seen for the (A1) to be awarded.
OR
\(\sqrt {{4^2} – {3^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
\( = \sqrt 7 \) (A1)
\( = 2.65{\text{ (cm)}}\) (AG)
Note: The exact answer must be seen for the final (A1) to be awarded.
(ii) \(\pi \times {3^2} \times 4.5 + \frac{1}{3}\pi \times {3^2} \times 2.65\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula, (M1) for correct substitution into the volume of a cone formula, (M1) for adding both of their volumes.
\( = 152{\text{ c}}{{\text{m}}^3}\;\;\;(152.210 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}48.45\pi {\text{ c}}{{\text{m}}^3})\) (A1)(G3)
\(\pi {3^2}h = 125\) (M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula.
Accept alternative methods. Accept \(4.43\) (\(4.42913 \ldots \)) from using rounded answers in \(h = \frac{{125 \times 4.5}}{{127}}\).
\(h = 4.42{\text{ (cm)}}\;\;\;\left( {4.42097 \ldots {\text{ (cm)}}} \right)\) (A1)(G2)
\(2\pi \times 3 \times 4.5 + \pi \times 3 \times 4 + \pi \times {3^2}\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into curved surface area of a cylinder formula, (M1) for correct substitution into the curved surface area of a cone formula, (M1) for adding the area of the base of the cylinder to the other two areas.
\( = 151{\text{ c}}{{\text{m}}^2}\;\;\;(150.796 \ldots {\text{ c}}{{\text{m}}^2},{\text{ }}48\pi {\text{ c}}{{\text{m}}^2})\) (A1)(G3)
\(\frac{{150.796 \ldots }}{7} \times 3\) (M1)(M1)
Notes: Award (M1) for dividing their answer to (c) by \(7\), (M1) for multiplying by \(3\). Accept equivalent methods.
\( = 64.63{\text{ (ZAR)}}\) (A1)(ft)(G2)
Notes: The (A1) is awarded for their correct answer, correctly rounded to 2 decimal places. Follow through from their answer to part (c). If rounded answer to part (c) is used the answer is \(64.71\) (ZAR).
\(\frac{{325}}{{13.03}}\) (M1)
Note: Award (M1) for dividing \(325\) by \(13.03\).
\( = 24.94{\text{ (EUR)}}\) (A1)(G2)
Note: The (A1) is awarded for the correct answer rounded to 2 decimal places, unless already penalized in part (d).
Question
The following table shows the number of bicycles, \(x\), produced daily by a factory and their total production cost, \(y\), in US dollars (USD). The table shows data recorded over seven days.
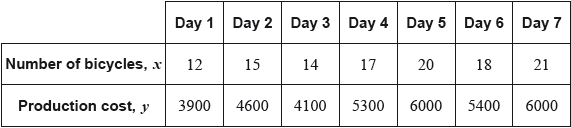
(i) Write down the Pearson’s product–moment correlation coefficient, \(r\), for these data.
(ii) Hence comment on the result.[4]
Write down the equation of the regression line \(y\) on \(x\) for these data, in the form \(y = ax + b\).[2]
Estimate the total cost, to the nearest USD, of producing \(13\) bicycles on a particular day.[3]
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
Explain why the factory does not make a profit when producing \(13\) bicycles on a particular day.[2]
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
(i) Write down an expression for the total selling price of \(x\) bicycles.
(ii) Write down an expression for the profit the factory makes when producing \(x\) bicycles on a particular day.
(iii) Find the least number of bicycles that the factory should produce, on a particular day, in order to make a profit.[5]
Answer/Explanation
Markscheme
(i) \(r = 0.985\;\;\;(0.984905 \ldots )\) (G2)
Notes: If unrounded answer is not seen, award (G1)(G0) for \(0.99\) or \(0.984\). Award (G2) for \(0.98\).
(ii) strong, positive (A1)(A1)
\(y = 259.909 \ldots x + 698.648 \ldots \;\;\;(y = 260x + 699)\) (G1)(G1)
Notes: Award (G1) for \(260x\) and (G1) for \(699\). If the answer is not an equation award a maximum of (G1)(G0).
\(y = 259.909 \ldots \times 13 + 698.648 \ldots \) (M1)
Note: Award (M1) for substitution of \(13\) into their regression line equation from part (b).
\(y = 4077.47 \ldots \) (A1)(ft)(G2)
\(y = 4077{\text{ (USD)}}\) (A1)(ft)
Notes: Follow through from their answer to part (b). If rounded values from part (b) used, answer is \(4079\). Award the final (A1)(ft) for a correct rounding to the nearest USD of their answer. The unrounded answer may not be seen.
If answer is \(4077\) and no working is seen, award (G2).
\(13 \times 304 – (4077.47) = – 125.477 \ldots \;\;\;( – 125)\;\;\;\)OR
\(4077.47 – (13 \times 304) = 125.477 \ldots \;\;\;(125)\) (M1)
Notes: Award (M1) for calculating the difference between \(13 \times 304\) and their answer to part (c).
If rounded values are used in equation, answer is \( – 127\).
profit is negative\(\;\;\;\)OR\(\;\;\;{\text{cost}} > {\text{sales}}\) (A1)
OR
\(13 \times 304 = 3952\) (M1)
Note: Award (M1) for calculating the price of \(13\) bikes.
\(3952 < 4077.47\) (A1)(ft)
Note: Award (A1) for showing \(3952\) is less than their part (c). This may be communicated in words. Follow through from part (c), but only if value is greater than \(3952\).
OR
\(\frac{{4077}}{{13}} = 313.62\) (M1)
Note: Award (M1) for calculating the cost of \(1\) bicycle.
\(313.62 > 304\) (A1)(ft)
Note: Award (A1) for showing \(313.62\) is greater than \(304\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(304\).
OR
\(\frac{{4077}}{{304}} = 13.41\) (M1)
Note: Award (M1) for calculating the number of bicycles that should have been be sold to cover total cost.
\(13.41 > 13\) (A1)(ft)
Note: Award (A1) for showing \(13.41\) is greater than \(13\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(13\).
(i) \(304x\) (A1)
(ii) \(304x – (259.909 \ldots x + 698.648 \ldots )\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for difference between their answers to parts (b) and (e)(i), (A1)(ft) for correct expression.
(iii) \(304x – (259.909 \ldots x + 698.648 \ldots ) > 0\) (M1)
Notes: Award (M1) for comparing their expression in part (e)(ii) to \(0\). Accept an equation. Accept \(3040x – y > 0\) or equivalent.
\(x = 16{\text{ bicycles}}\) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b). Answer must be a positive integer greater than \(13\) for the (A1)(ft) to be awarded.
Award (G1) for an answer of \(15.84\).
Question
The line \({L_1}\) has equation \(2y – x – 7 = 0\) and is shown on the diagram.
The point A has coordinates \((1,{\text{ }}4)\).
The point C has coordinates \((5,{\text{ }}12)\). M is the midpoint of AC.
The straight line, \({L_2}\), is perpendicular to AC and passes through M.
The point D is the intersection of \({L_1}\) and \({L_2}\).
The length of MD is \(\frac{{\sqrt {45} }}{2}\).
The point B is such that ABCD is a rhombus.
Show that A lies on \({L_1}\).[2]
Find the coordinates of M.[2]
Find the length of AC.[2]
Show that the equation of \({L_2}\) is \(2y + x – 19 = 0\).[5]
Find the coordinates of D.[2]
Write down the length of MD correct to five significant figures.[1]
Find the area of ABCD.[3]
Answer/Explanation
Markscheme
\(2 \times 4 – 1 – 7 = 0\) (or equivalent) (R1)
Note: For (R1) accept substitution of \(x = 1\) or \(y = 4\) into the equation followed by a confirmation that \(y = 4\) or \(x = 1\).
(since the point satisfies the equation of the line,) A lies on \({L_1}\) (A1)
Note: Do not award (A1)(R0).[2 marks]
\(\frac{{1 + 5}}{2}\) OR \(\frac{{4 + 12}}{2}\) seen (M1)
Note: Award (M1) for at least one correct substitution into the midpoint formula.
\((3,{\text{ }}8)\) (A1)(G2)
Notes: Accept \(x = 3,{\text{ }}y = 8\).
Award (M1)(A0) for \(\left( {\frac{{1 + 5}}{2},{\text{ }}\frac{{4 + 12}}{2}} \right)\).
Award (G1) for each correct coordinate seen without working.[2 marks]
\(\sqrt {{{(5 – 1)}^2} + {{(12 – 4)}^2}} \) (M1)
Note: Award (M1) for a correct substitution into distance between two points formula.
\( = 8.94{\text{ }}\left( {4\sqrt 5 ,{\text{ }}\sqrt {80} ,{\text{ }}8.94427 \ldots } \right)\) (A1)(G2)[2 marks]
gradient of \({\text{AC}} = \frac{{12 – 4}}{{5 – 1}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = 2\) (A1)
Note: Award (M1)(A1) for gradient of \({\text{AC}} = 2\) with or without working
gradient of the normal \( = – \frac{1}{2}\) (M1)
Note: Award (M1) for the negative reciprocal of their gradient of AC.
\(y – 8 = – \frac{1}{2}(x – 3)\) OR \(8 = – \frac{1}{2}(3) + c\) (M1)
Note: Award (M1) for substitution of their point and gradient into straight line formula. This (M1) can only be awarded where \( – \frac{1}{2}\) (gradient) is correctly determined as the gradient of the normal to AC.
\(2y – 16 = – (x – 3)\) OR \( – 2y + 16 = x – 3\) OR \(2y = – x + 19\) (A1)
Note: Award (A1) for correctly removing fractions, but only if their equation is equivalent to the given equation.
\(2y + x – 19 = 0\) (AG)
Note: The conclusion \(2y + x – 19 = 0\) must be seen for the (A1) to be awarded.
Where the candidate has shown the gradient of the normal to \({\text{AC}} = – 0.5\), award (M1) for \(2(8) + 3 – 19 = 0\) and (A1) for (therefore) \(2y + x – 19 = 0\).
Simply substituting \((3,{\text{ }}8)\) into the equation of \({L_2}\) with no other prior working, earns no marks.[5 marks]
\((6,{\text{ }}6.5)\) (A1)(A1)(G2)
Note: Award (A1) for 6, (A1) for 6.5. Award a maximum of (A1)(A0) if answers are not given as a coordinate pair. Accept \(x = 6,{\text{ }}y = 6.5\).
Award (M1)(A0) for an attempt to solve the two simultaneous equations \(2y – x – 7 = 0\) and \(2y + x – 19 = 0\) algebraically, leading to at least one incorrect or missing coordinate.[2 marks]
3.3541 (A1)
Note: Answer must be to 5 significant figures.[1 mark]
\(2 \times \frac{1}{2} \times \sqrt {80} \times \frac{{\sqrt {45} }}{2}\) (M1)(M1)
Notes: Award (M1) for correct substitution into area of triangle formula.
If their triangle is a quarter of the rhombus then award (M1) for multiplying their triangle by 4.
If their triangle is a half of the rhombus then award (M1) for multiplying their triangle by 2.
OR
\(\frac{1}{2} \times \sqrt {80} \times \sqrt {45} \) (M1)(M1)
Notes: Award (M1) for doubling MD to get the diagonal BD, (M1) for correct substitution into the area of a rhombus formula.
Award (M1)(M1) for \(\sqrt {80} \times \) their (f).
\( = 30\) (A1)(ft)(G3)
Notes: Follow through from parts (c) and (f).
\(8.94 \times 3.3541 = 29.9856 \ldots \)[3 marks]
Question
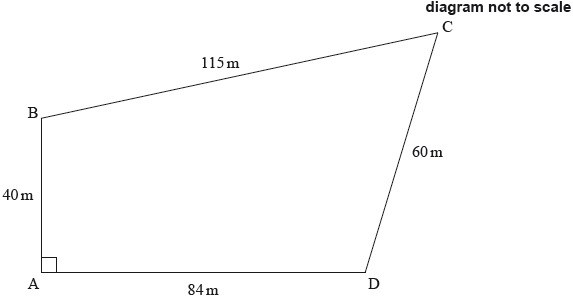
Abdallah owns a plot of land, near the river Nile, in the form of a quadrilateral ABCD.
The lengths of the sides are \({\text{AB}} = {\text{40 m, BC}} = {\text{115 m, CD}} = {\text{60 m, AD}} = {\text{84 m}}\) and angle \({\rm{B\hat AD}} = 90^\circ \).
This information is shown on the diagram.
The formula that the ancient Egyptians used to estimate the area of a quadrilateral ABCD is
\({\text{area}} = \frac{{({\text{AB}} + {\text{CD}})({\text{AD}} + {\text{BC}})}}{4}\).
Abdallah uses this formula to estimate the area of his plot of land.
Show that \({\text{BD}} = 93{\text{ m}}\) correct to the nearest metre.[2]
Calculate angle \({\rm{B\hat CD}}\).[3]
Find the area of ABCD.[4]
Calculate Abdallah’s estimate for the area.[2]
Find the percentage error in Abdallah’s estimate.[2]
Answer/Explanation
Markscheme
\({\text{B}}{{\text{D}}^2} = {40^2} + {84^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras.
Accept correct substitution into cosine rule.
\({\text{BD}} = 93.0376 \ldots \) (A1)
\( = 93\) (AG)
Note: Both the rounded and unrounded value must be seen for the (A1) to be awarded.[2 marks]
\(\cos C = \frac{{{{115}^2} + {{60}^2} – {{93}^2}}}{{2 \times 115 \times 60}}{\text{ }}({93^2} = {115^2} + {60^2} – 2 \times 115 \times 60 \times \cos C)\) (M1)(A1)
Note: Award (M1) for substitution into cosine formula, (A1) for correct substitutions.
\( = 53.7^\circ {\text{ }}(53.6679 \ldots ^\circ )\) (A1)(G2)[3 marks]
\(\frac{1}{2}(40)(84) + \frac{1}{2}(115)(60)\sin (53.6679 \ldots )\) (M1)(M1)(A1)(ft)
Note: Award (M1) for correct substitution into right-angle triangle area. Award (M1) for substitution into area of triangle formula and (A1)(ft) for correct substitution.
\( = 4460{\text{ }}{{\text{m}}^2}{\text{ }}(4459.30 \ldots {\text{ }}{{\text{m}}^2})\) (A1)(ft)(G3)
Notes: Follow through from part (b).[4 marks]
\(\frac{{(40 + 60)(84 + 115)}}{4}\) (M1)
Note: Award (M1) for correct substitution in the area formula used by ‘Ancient Egyptians’.
\( = 4980{\text{ }}{{\text{m}}^2}{\text{ }}(4975{\text{ }}{{\text{m}}^2})\) (A1)(G2)[2 marks]
\(\left| {\frac{{4975 – 4459.30 \ldots }}{{4459.30 \ldots }}} \right| \times 100\) (M1)
Notes: Award (M1) for correct substitution into percentage error formula.
\( = 11.6{\text{ }}(\% ){\text{ }}(11.5645 \ldots )\) (A1)(ft)(G2)
Notes: Follow through from parts (c) and (d)(i).[2 marks]
Question
The Tower of Pisa is well known worldwide for how it leans.
Giovanni visits the Tower and wants to investigate how much it is leaning. He draws a diagram showing a non-right triangle, ABC.
On Giovanni’s diagram the length of AB is 56 m, the length of BC is 37 m, and angle ACB is 60°. AX is the perpendicular height from A to BC.
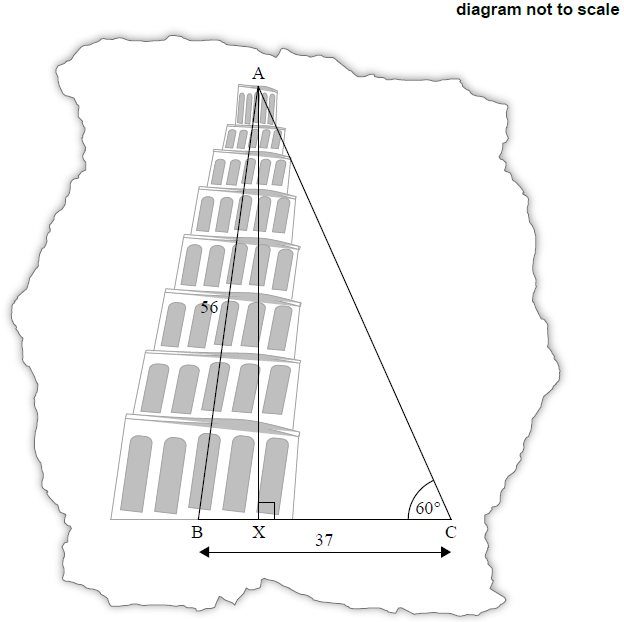
Giovanni’s tourist guidebook says that the actual horizontal displacement of the Tower, BX, is 3.9 metres.
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree.[5]
Use Giovanni’s diagram to calculate the length of AX.[2]
Use Giovanni’s diagram to find the length of BX, the horizontal displacement of the Tower.[2]
Find the percentage error on Giovanni’s diagram.[2]
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.
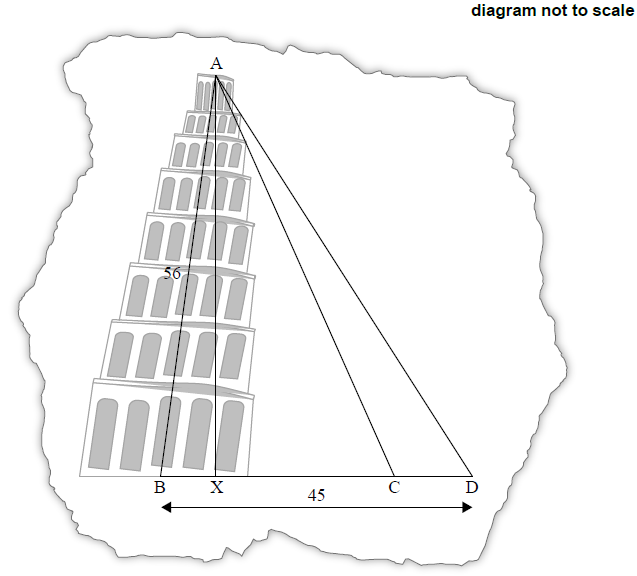
Find the angle of elevation of A from D.[3]
Answer/Explanation
Markscheme
\(\frac{{{\text{sin BAC}}}}{{37}} = \frac{{{\text{sin 60}}}}{{56}}\) (M1)(A1)
Note: Award (M1) for substituting the sine rule formula, (A1) for correct substitution.
angle \({\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}\) = 34.9034…° (A1)
Note: Award (A0) if unrounded answer does not round to 35. Award (G2) if 34.9034… seen without working.
angle \({\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}\) = 180 − (34.9034… + 60) (M1)
Note: Award (M1) for subtracting their angle BAC + 60 from 180.
85.0965…° (A1)
85° (AG)
Note: Both the unrounded and rounded value must be seen for the final (A1) to be awarded. If the candidate rounds 34.9034…° to 35° while substituting to find angle \({\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}\), the final (A1) can be awarded but only if both 34.9034…° and 35° are seen.
If 85 is used as part of the workings, award at most (M1)(A0)(A0)(M0)(A0)(AG). This is the reverse process and not accepted.
sin 85… × 56 (M1)
= 55.8 (55.7869…) (m) (A1)(G2)
Note: Award (M1) for correct substitution in trigonometric ratio.
\(\sqrt {{{56}^2} – 55.7869{ \ldots ^2}} \) (M1)
Note: Award (M1) for correct substitution in the Pythagoras theorem formula. Follow through from part (a)(ii).
OR
cos(85) × 56 (M1)
Note: Award (M1) for correct substitution in trigonometric ratio.
= 4.88 (4.88072…) (m) (A1)(ft)(G2)
Note: Accept 4.73 (4.72863…) (m) from using their 3 s.f answer. Accept equivalent methods.[2 marks]
\(\left| {\frac{{4.88 – 3.9}}{{3.9}}} \right| \times 100\) (M1)
Note: Award (M1) for correct substitution into the percentage error formula.
= 25.1 (25.1282) (%) (A1)(ft)(G2)
Note: Follow through from part (a)(iii).[2 marks]
\({\text{ta}}{{\text{n}}^{ – 1}}\left( {\frac{{55.7869 \ldots }}{{40.11927 \ldots }}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their 40.11927… seen. Award (M1) for correct substitution into trigonometric ratio.
OR
(37 − 4.88072…)2 + 55.7869…2
(AC =) 64.3725…
64.3726…2 + 82 − 2 × 8 × 64.3726… × cos120
(AD =) 68.7226…
\(\frac{{{\text{sin 120}}}}{{68.7226 \ldots }} = \frac{{{\text{sin A}}\mathop {\text{D}}\limits^ \wedge {\text{C}}}}{{64.3725 \ldots }}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their correct values seen, (M1) for correct substitution into the sine formula.
= 54.3° (54.2781…°) (A1)(ft)(G2)
Note: Follow through from part (a). Accept equivalent methods.[3 marks]
Question
The Brahma chicken produces eggs with weights in grams that are normally distributed about a mean of \(55{\text{ g}}\) with a standard deviation of \(7{\text{ g}}\). The eggs are classified as small, medium, large or extra large according to their weight, as shown in the table below.
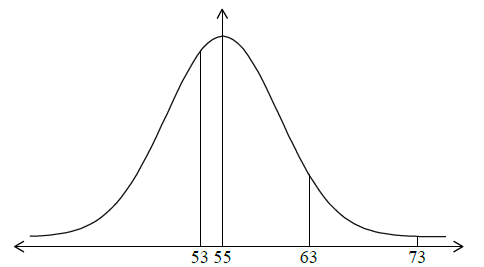
Sketch a diagram of the distribution of the weight of Brahma chicken eggs. On your diagram, show clearly the boundaries for the classification of the eggs.[3]
An egg is chosen at random. Find the probability that the egg is
(i) medium;
(ii) extra large.[4]
There is a probability of \(0.3\) that a randomly chosen egg weighs more than \(w\) grams.
Find \(w\) .[2]
The probability that a Brahma chicken produces a large size egg is \(0.121\). Frank’s Brahma chickens produce \(2000\) eggs each month.
Calculate an estimate of the number of large size eggs produced by Frank’s chickens each month.[2]
The selling price, in US dollars (USD), of each size is shown in the table below.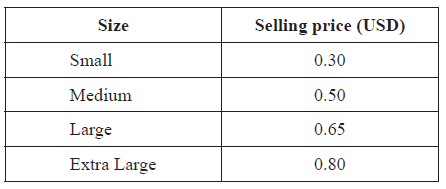
The probability that a Brahma chicken produces a small size egg is \(0.388\).
Estimate the monthly income, in USD, earned by selling the \(2000\) eggs. Give your answer correct to two decimal places.[3]
Answer/Explanation
Markscheme
(A1) for normal curve with mean of \(55\) indicated
(A1) for three lines in approximately the correct position
(A1) for labels on the three lines (A1)(A1)(A1)
(i) \({\text{P}}(53 \leqslant {\text{Weight}} < 63) = 0.486\) (\(0.485902 \ldots \)) (M1)(A1)(G2)
Note: Award (M1) for correct region indicated on labelled diagram.
(ii) \({\text{P}}({\text{Weight}} > 73) = 0.00506\) (\(0.00506402\)) (M1)(A1)(G2)
Note: Award (M1) for correct region indicated on labelled diagram.
\({\text{P}}({\text{Weight}} > w) = 0.3\) (M1)
\(w = 58.7\) (\(58.6708 \ldots \)) (A1)(G2)
Note: Award (M1) for correct region indicated on labelled diagram.
Expected number of large size eggs
\( = 2000(0.121)\) (M1)
\( = 242\) (A1)(G2)
Expected income
\( = 2000 \times 0.30 \times 0.388 + 2000 \times 0.50 \times 0.486 + 2000 \times 0.65 \times 0.121 + 2000 \times 0.80 \times 0.00506\) (M1)(M1)
Note: Award (M1) for their correct products, (M1) for addition of 4 terms.
\( = 884.20{\text{ USD}}\) (A1)(ft)(G3)
Note: Follow through from part (b).