Question
Five pipes labelled, “6 metres in length”, were delivered to a building site. The contractor measured each pipe to check its length (in metres) and recorded the following;
5.96, 5.95, 6.02, 5.95, 5.99.
(i) Find the mean of the contractor’s measurements.
(ii) Calculate the percentage error between the mean and the stated, approximate length of 6 metres.[3]
Calculate \(\sqrt {{{3.87}^5} – {{8.73}^{ – 0.5}}} \), giving your answer
(i) correct to the nearest integer,
(ii) in the form \(a \times 10^k\), where 1 ≤ a < 10, \(k \in {\mathbb{Z}}\) .[3]
Answer/Explanation
Markscheme
(i) Mean = (5.96 + 5.95 + 6.02 + 5.95 + 5.99) / 5 = 5.974 (5.97) (A1)
(ii) \({\text{% error}} = \frac{{error}}{{actualvalue}} \times 100\% \)
\( = \frac{{6 – 5.974}}{{5.974}} \times 100\% = 0.435\% \) (M1)(A1)(ft)
(M1) for correctly substituted formula.
Allow 0.503% as follow through from 5.97
Note: An answer of 0.433% is incorrect. (C3)
[3 marks]
number is 29.45728613
(i) Nearest integer = 29 (A1)
(ii) Standard form = 2.95 × 101 (accept 2.9 × 101) (A1)(ft)(A1)
Award (A1) for each correct term
Award (A1)(A0) for 2.95 × 10 (C3)
[3 marks]
Question
Calculate \(\frac{{77.2 \times {3^3}}}{{3.60 \times {2^2}}}\).[1]
Express your answer to part (a) in the form \(a \times 10^k\), where \(1 \leqslant a < 10\) and \(k \in {\mathbb{Z}}\).[2]
Juan estimates the length of a carpet to be 12 metres and the width to be 8 metres. He then estimates the area of the carpet.
(i) Write down his estimated area of the carpet.
When the carpet is accurately measured it is found to have an area of 90 square metres.
(ii) Calculate the percentage error made by Juan.[3]
Answer/Explanation
Markscheme
\(144.75\left( { = \frac{{579}}{4}} \right)\) (A1)
accept 145 (C1)
[1 mark]
\(1.4475 \times 10^2\) (A1)(ft)(A1)(ft)
accept \(1.45 \times 10^2\) (C2)
[2 marks]
Unit penalty (UP) is applicable in question part (c)(i) only.
(UP) (i) Area = 96 m2 (A1)
(ii) \(\% {\text{ error}} = \frac{{(96 – 90)}}{{90}} \times 100\) (M1)
\( = \frac{{6 \times 100}}{{90}}\)
\(\frac{{20}}{3}\% \) or 6.67 % (A1)(ft) (C3)
[3 marks]
Question
Calculate exactly \(\frac{{{{(3 \times 2.1)}^3}}}{{7 \times 1.2}}\).[1]
Write the answer to part (a) correct to 2 significant figures.[1]
Calculate the percentage error when the answer to part (a) is written correct to 2 significant figures.[2]
Write your answer to part (c) in the form \(a \times {10^k}\) where \(1 \leqslant a < 10{\text{ and }}k \in \mathbb{Z}\).[2]
Answer/Explanation
Markscheme
\(29.7675\) (A1) (C1)
Note: Accept exact answer only.
[1 mark]
\(30\) (A1)(ft) (C1)
[1 mark]
\(\frac{{30 – 29.7675}}{{29.7675}} \times 100\% \) (M1)
For correct formula with correct substitution.
\( = 0.781\% \) accept \(0.78\% \) only if formula seen with \(29.7675\) as denominator (A1)(ft) (C2)
[2 marks]
\(7.81 \times {10^{ – 1}}\% \) (\(7.81 \times {10^{ – 3}}\) with no percentage sign) (A1)(ft)(A1)(ft) (C2)
[2 marks]
Question
The diagram shows triangle ABC in which angle BAC \( = 30^\circ \), BC \( = 6.7\) cm and AC \( = 13.4\) cm.
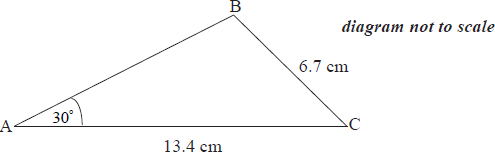
Calculate the size of angle ACB.[4]
Nadia makes an accurate drawing of triangle ABC. She measures angle BAC and finds it to be 29°.
Calculate the percentage error in Nadia’s measurement of angle BAC.[2]
Answer/Explanation
Markscheme
\(\frac{{\sin {\text{A}}{\operatorname{\hat B}}{\text{C}}}}{{13.4}} = \frac{{\sin 30^\circ }}{{6.7}}\) (M1)(A1)
Note: Award (M1) for correct substituted formula, (A1) for correct substitution.
\({\text{A}}{\operatorname{\hat B}}{\text{C}}\) = 90° (A1)
\({\text{A}}{\operatorname{\hat C}}{\text{B}}\) = 60° (A1)(ft) (C4)
Note: Radians give no solution, award maximum (M1)(A1)(A0).
[4 marks]
\(\frac{{29 – 30}}{{30}} \times 100\) (M1)
Note: Award (M1) for correct substitution into correct formula.
% error = −33.3 % (A1) (C2)
Notes: Percentage symbol not required. Accept positive answer.
[2 marks]
Question
The following diagram shows a rectangle with sides of length 9.5 ×102 m and 1.6 ×103 m.
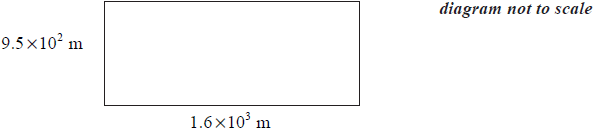
Write down the area of the rectangle in the form a × 10k, where 1 ≤ a < 10, k ∈ \(\mathbb{Z}\).[3]
Helen’s estimate of the area of the rectangle is \(1\,600\,000{\text{ }}{{\text{m}}^2}\).
Find the percentage error in Helen’s estimate.[3]
Answer/Explanation
Markscheme
UP applies in part (a).
\(9.5 \times 10^2 \times 1.6 \times 10^3\) (M1)
(UP) \( = 1.52 \times {10^6}{\text{ }}{{\text{m}}^2}\) (A1)(A1) (C3)
Notes: Award (M1) for multiplication of the two numbers.
Award (A1) for \(1.52\), (A1) for \(10^6\).
[3 marks]
\(\frac{{1600000 – 1520000}}{{1520000}} \times 100\) (M1)(A1)(ft)
Note: Award (M1) for substitution in formula, (A1)(ft) for their correct substitution.
= 5.26 % (percent sign not required). (A1)(ft) (C3)
Note: Accept positive or negative answer.
[3 marks]
Question
A shipping container is a cuboid with dimensions \({\text{16 m}}\), \({\text{1}}\frac{{\text{3}}}{{\text{4}}}{\text{ m}}\) and \({\text{2}}\frac{{\text{2}}}{{\text{3}}}{\text{ m}}\).
Calculate the exact volume of the container. Give your answer as a fraction.[3]
Jim estimates the dimensions of the container as 15 m, 2 m and 3 m and uses these to estimate the volume of the container.
Calculate the percentage error in Jim’s estimated volume of the container.[3]
Answer/Explanation
Markscheme
\(V = 16 \times 1\frac{3}{4} \times 2\frac{2}{3}\) (M1)
Note: Award (M1) for correct substitution in volume formula. Accept decimal substitution of \(2.66\) or better.
\( = 74.6666{\text{ }} \ldots \) (A1)
\( = {\text{74}}\frac{{\text{2}}}{{\text{3}}}{\text{ }}{{\text{m}}^{\text{3}}}{\text{ }}\left( {\frac{{{\text{224}}}}{{\text{3}}}{\text{ }}{{\text{m}}^{\text{3}}}} \right)\) (A1) (C3)
Note: Correct answer only.
[3 marks]
\({\text{% error}} = \frac{{\left( {90 – 74\frac{2}{3}} \right) \times 100}}{{74\frac{2}{3}}}\) (A1)(M1)
Note: Award (A1) for \(90\) seen, or inferred in numerator, (M1) for correct substitution into percentage error formula.
\( = 20.5\) (A1)(ft) (C3)
Note: Accept \( – 20.5\).
[3 marks]
Question
José stands 1.38 kilometres from a vertical cliff.
Express this distance in metres.[1]
José estimates the angle between the horizontal and the top of the cliff as 28.3° and uses it to find the height of the cliff.
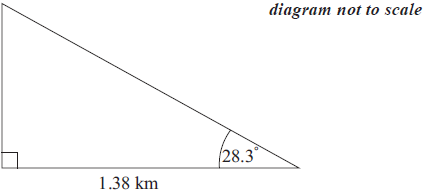
Find the height of the cliff according to José’s calculation. Express your answer in metres, to the nearest whole metre.[3]
José estimates the angle between the horizontal and the top of the cliff as 28.3° and uses it to find the height of the cliff.
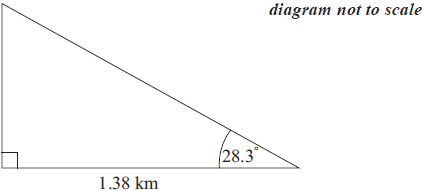
The actual height of the cliff is 718 metres. Calculate the percentage error made by José when calculating the height of the cliff.[2]
Answer/Explanation
Markscheme
1380 (m) (A1) (C1)[1 mark]
\(1380\tan 28.3\) (M1)
\( = 743.05 \ldots \) . (A1)(ft)
\( = 743\) (m) (A1)(ft) (C3)
Notes: Award (M1) for correct substitution in tan formula or equivalent, (A1)(ft) for their 743.05 seen, (A1)(ft) for their answer correct to the nearest m.[3 marks]
\({\text{percentage error}} = \frac{{743.05 \ldots – 718}}{{718}} \times 100\) (M1)
Note: Award (M1) for correct substitution in formula.
= 3.49 % (% symbol not required) (A1)(ft) (C2)
Notes: Accept 3.48 % for use of 743.
Accept negative answer.[2 marks]
Question
In a television show there is a transparent box completely filled with identical cubes. Participants have to estimate the number of cubes in the box. The box is 50 cm wide, 100 cm long and 40 cm tall.
Find the volume of the box.[2]
Joaquin estimates the volume of one cube to be 500 cm3. He uses this value to estimate the number of cubes in the box.
Find Joaquin’s estimated number of cubes in the box.[2]
The actual number of cubes in the box is 350.
Find the percentage error in Joaquin’s estimated number of cubes in the box.[2]
Answer/Explanation
Markscheme
\(50 \times 100 \times 40 = 200\,000{\text{ c}}{{\text{m}}^3}\) (M1)(A1) (C2)
Note: Award (M1) for correct substitution in the volume formula.
[2 marks]
\(\frac{{200\,000}}{{500}} = 400\) (M1)(A1)(ft) (C2)
Note: Award (M1) for dividing their answer to part (a) by 500.
[2 marks]
\(\frac{{400 – 350}}{{350}} \times 100 = 14.3{\text{ }}\% \) (M1)(A1)(ft) (C2)
Notes: Award (M1) for correct substitution in the percentage error formula.
Award (A1) for answer, follow through from part (b).
Accept –14.3 %.
% sign not necessary.
[2 marks]
Question
Given \(p = x – \frac{{\sqrt y }}{z}\) , \(x = 1.775\) , \(y = 1.44\) and \(z = 48\) .
Calculate the value of \(p\).[2]
Barry first writes \(x\) , \(y\) and \(z\) correct to one significant figure and then uses these values to estimate the value of \(p\) .
(i) Write down \(x\) , \(y\) and \(z\) each correct to one significant figure.
(ii) Write down Barry’s estimate of the value of \(p\) .[2]
Calculate the percentage error in Barry’s estimate of the value of \(p\) .[2]
Answer/Explanation
Markscheme
\(p = 1.775 – \frac{{\sqrt {1.44} }}{{48}}\) (M1)
Note: Award (M1) for correctly substituted equation for \(p\).
\( = 1.75\) \(\left( {1.750{\text{, }}\frac{7}{4}} \right)\) (A1)(C2)
[2 marks]
(i) \(x = 2\), \(y =1\), \(z = 50\) (A1)
(ii) \(p =1.98\) \(\left( {\frac{{99}}{{50}}} \right)\) (A1)(ft) (C2)
Note: Follow through from part (b)(i), irrespective of whether working is shown.
Note: If 2 s.f. used throughout part (b)(i) award (A1)(ft) for \(1.78\) or \(1.8\).
[2 marks]
\(\frac{{1.98 – 1.75}}{{1.75}} \times 100\) (M1)
Note: Award (M1) for correctly substituted \(\% \) error formula.
Note: Follow through from parts (a) and (b).
\( = 13.1\% \) (A1)(ft) (C2)
Notes: \(\% \) sign not required. Do not accept \( – 13.1\% \). If 100 missing and incorrect answer, award (M0)(A0). If 100 missing and answer incorrectly rounded, award (M1)(A1).
[2 marks]
Question
\(80\) matches were played in a football tournament. The following table shows the number of goals scored in all matches.
Find the mean number of goals scored per match.[2]
Find the median number of goals scored per match.[2]
A local newspaper claims that the mean number of goals scored per match is two. Calculate the percentage error in the local newspaper’s claim.[2]
Answer/Explanation
Markscheme
\(\frac{{0 \times 16 + 1 \times 22 + 2 \times 19 \ldots }}{{80}}\) (M1)
Note: Award (M1) for substituting correct values into mean formula.
1.75 (A1) (C2)[2 marks]
An attempt to enumerate the number of goals scored. (M1)
\(2\) (A1) (C2)[2 marks]
\(\frac{{2 – 1.75}}{{1.75}} \times 100\) (M1)
\(14.3 \% \) (A1)(ft) (C2)
Notes: Award (M1) for correctly substituted \(\% \) error formula. \(\% \) sign not required. Follow through from their answer to part (a). If \(100\) is missing and answer incorrect award (M0)(A0). If \(100\) is missing and answer incorrectly rounded award (M1)(A1)(ft)(AP).[2 marks]
Question
The length, in cm, of six baseball bats was measured. The lengths are given below.
104.5, 105.1, 104.8, 105.2, 104.9, 104.9
Calculate the exact value of the mean length.[2]
Write your answer to part (a) in the form a × 10k where 1 ≤ a < 10 and \(k \in \mathbb{Z}\).[2]
Marian calculates the mean length and finds it to be 105 cm.
Calculate the percentage error made by Marian.[2]
Answer/Explanation
Markscheme
\(\left( {\frac{{104.5 + 105.1 + …}}{6}} \right)\) (M1)
Note: Award (M1) for use of mean formula.
= 104.9 (cm) (A1) (C2)[2 marks]
1.049 × 102 (A1)(ft)(A1)(ft) (C2)
Notes: Award (A1)(ft) for 1.049, (A1)(ft) for 102. Follow through from their part (a).[2 marks]
\(\frac{{105 – 104.9}}{{104.9}} \times 100\) (%) (M1)
Notes: Award (M1) for their correctly substituted % error formula.
% error = 0.0953 (%) (0.0953288…) (A1)(ft) (C2)
Notes: A 2sf answer of 0.095 following \(\frac{{105 – 104.9}}{{105}} \times 100\) working is awarded no marks. Follow through from their part (a), provided it is not 105. Do not accept a negative answer. % sign not required.[2 marks]
Question
Ludmila takes a loan of 320 000 Brazilian Real (BRL) from a bank for two years at a nominal annual interest rate of 10%, compounded half yearly.
Write down the number of times interest is added to the loan in the two years.[1]
Calculate the exact amount of money that Ludmila must repay at the end of the two years.[3]
Ludmila estimates that she will have to repay \({\text{360}}\,{\text{000}}\) BRL at the end of the two years.
Calculate the percentage error in her estimate.[2]
Answer/Explanation
Markscheme
4 (A1) (C1)[1 mark]
\(320\,000{\left( {1 + \frac{{10}}{{2 \times 100}}} \right)^{2 \times 2}}\) (M1)(A1)
Note: Award (M1) for substituted compound interest formula, (A1) for correct substitutions.
OR
\({\text{N}} = 2\)
\({\text{I}}\% = 10\)
\({\text{PV}} = – 320000\)
\({\text{P }}/{\text{ Y}} = 1\)
\({\text{C }}/{\text{ Y}} = 2\) (A1)(M1)
Note: Award (A1) for \({\text{C }}/{\text{ Y}} = 2\) seen, (M1) for correctly substituted values from the question into the finance application.
OR
\({\text{N}} = 4\)
\({\text{I}}\% = 10\)
\({\text{PV}} = – 320000\)
\({\text{P }}/{\text{ Y}} = 2\)
\({\text{C }}/{\text{ Y}} = 2\) (A1)(M1)
Note: Award (A1) for \({\text{C }}/{\text{ Y}} = 2\) seen, (M1) for correctly substituted values from the question into the finance application.
amount to repay \( = 388962\) (A1) (C3)
Note: Award (C2) for final answer \(389000\) if \(388962\) not seen previously.[3 marks]
\(\left| {\frac{{360\,000 – 388\,962}}{{388\,962}}} \right| \times 100\) (M1)
Note: Award (M1) for correctly substituted percentage error formula.
\( = 7.45{\text{ (% ) }}(7.44597 \ldots )\) (A1)(ft) (C2)
Notes: Follow through from their answer to part (b).[2 marks]
Question
\(T = \frac{{\left( {\tan (2z) + 1} \right)\left( {2\cos (z) – 1} \right)}}{{{y^2} – {x^2}}}\), where \(x = 9\), \(y = 41\) and \(z = 30^\circ \).
Calculate the exact value of \(T\).[2]
Give your answer to \(T\) correct to
(i) two significant figures;
(ii) three decimal places.[2]
Pyotr estimates the value of \(T\) to be \(0.002\).
Calculate the percentage error in Pyotr’s estimate.[2]
Answer/Explanation
Markscheme
\(\frac{{\left( {\tan (2 \times 30) + 1} \right)\left( {2\cos (30) – 1} \right)}}{{{{41}^2} – {9^2}}}\) (M1)
Note: Award (M1) for correct substitution into formula.
\( = 0.00125\;\;\;\left( {\frac{1}{{800}}} \right)\) (A1) (C2)
Note: Using radians the answer is \( – 0.000570502\), award at most (M1)(A0).
(i) \(0.0013\) (A1)(ft)
Note: Follow through from part (a).
(ii) \(0.001\) (A1)(ft) (C2)
Note: Follow through from part (a).
\(\left| {\frac{{0.002 – 0.00125}}{{0.00125}}} \right| \times 100\) (M1)
Notes: Award (M1) for their correct substitution into the percentage error formula. Absolute value signs are not required.
Their unrounded answer from part (a) must be used.
Do not accept use of answers from part (b).
\( = 60{\text{ (%)}}\) (A1)(ft) (C2)
Notes: The \({\text{%}}\) sign is not required.
The answer from radians is \(450.568{\text{%}}\), award (M1)(A1)(ft).
Follow through from part (a).
Question
Fabián stands on top of a building, T, which is on a horizontal street.
He observes a car, C, on the street, at an angle of depression of 30°. The base of the building is at B. The height of the building is 80 metres.
The following diagram indicates the positions of T, B and C.
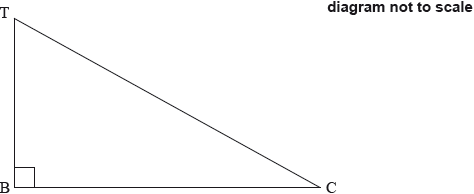
Show, in the appropriate place on the diagram, the values of
(i) the height of the building;
(ii) the angle of depression.[2]
Find the distance, BC, from the base of the building to the car.[2]
Fabián estimates that the distance from the base of the building to the car is 150 metres. Calculate the percentage error of Fabián’s estimate.[2]
Answer/Explanation
Markscheme
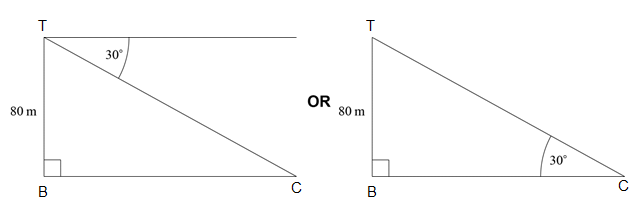(A1)(A1) (C2)
Notes: Award (A1) for 80 m in the correct position on diagram.
Award (A1) for 30° in a correct position on diagram.
\(\tan 30^\circ = \frac{{80}}{{{\text{BC}}}}\;\;\;\)OR\(\;\;\;\tan 60^\circ = \frac{{{\text{BC}}}}{{80}}\;\;\;\)OR\(\;\;\;\frac{{80}}{{\sin 30^\circ }} = \frac{{{\text{BC}}}}{{\sin 60^\circ }}\) (M1)
Note: Award (M1) for a correct trigonometric or Pythagorean equation for BC with correctly substituted values.
\(({\text{BC}} = ){\text{ 139 (m)}}\;\;\;\left( {138.564 \ldots {\text{ (m)}}} \right)\) (A1)(ft) (C2)
Notes: Accept an answer of \(80\sqrt 3 \) which is the exact answer.
Follow through from part (a).
Do not penalize use of radians unless it leads to a negative answer.
\(\left| {\frac{{150 – 138.564 \ldots }}{{138.564 \ldots }}} \right| \times 100\) (M1)
Notes: Award (M1) for their correct substitution into the percentage error formula.
\( = 8.25(\% )\;\;\;(8.25317 \ldots \% )\) (A1)(ft) (C2)
Notes: Accept \(7.91(\%)\) (\(7.91366…\) if \(139\) is used.
Accept \(8.23(\%)\) (\(8.22510…\) if \(138.6\) is used.
Follow through from their answer to part (b).
If answer to part (b) is \(46.2\), answer to part (c) is \(225\%\), award (M1)(A1)(ft) with or without working seen. If answer to part (b) is negative, award at most (M1)(A0).