Download IITian Academy App for accessing Online Mock Tests and More..
Question
Consider the statement \(p \Rightarrow q\).
If I break my arm, then it will hurt.
Write down in words, the inverse of \(p \Rightarrow q\).[2]
Complete the following truth table.
[2]
State whether the converse and the inverse of an implication are logically equivalent.
Justify your answer.[2]
Answer/Explanation
Markscheme
If I do not break my arm, then it will not hurt (A1)(A1) (C2)
Note: Award (A1) for “if… then…”
For Spanish candidates, only accept “Si” and “entonces”.
Award (A1) for “not break my arm” and “not hurt” in correct order.
(A1)(A1) (C2)
Notes: Award (A1) for each correct column.
logically equivalent (A1)(ft)
last two columns of the truth table are identical (R1)(ft) (C2)
Notes: Do not award (A1)(ft)(R0).
Follow through from the last two columns of the table in part (a).
Question
Consider the propositions \(r\), \(p\) and \(q\).
Complete the following truth table.
[4]
Determine whether the compound proposition \(\neg \left( {(r \wedge p) \vee \neg q)} \right) \Leftrightarrow \neg (r \wedge p) \wedge q\) is a tautology, a contradiction or neither.
Give a reason.[2]
Answer/Explanation
Markscheme
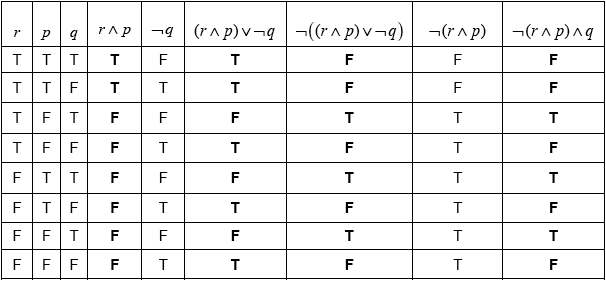(A1)(A1)(ft)(A1)(ft)(A1) (C4)
Notes: Award (A1) for each correct column.
For the “\({(r \wedge p) \vee \neg q}\)” follow through from the “\(r \wedge p\)” column.
For the “\(\neg \left( {(r \wedge p) \vee \neg q)} \right)\)” column, follow through from the preceding column.
tautology (A1)(ft)
columns \(\neg \left( {(r \wedge p) \vee \neg q)} \right)\) and \(\neg (r \wedge p) \wedge q\) are identical (R1)(C2)
Notes: Do not award (R0)(A1)(ft). Follow through from their table in part (a).
Award the (R1) for an additional column representing \(\neg \left( {(r \wedge p) \vee \neg q)} \right) \Leftrightarrow \neg (r \wedge p) \wedge q\) that is consistent with their table.
Question
\(p:x\) is a multiple of \(12\)
\(q:x\) is a multiple of \(6\).
Write down in words \(\neg p\).[1]
Write down in symbolic form the compound statement
\(r:\) If \(x\) is a multiple of \(12\), then \(x\) is a multiple of \(6\).[2]
Consider the compound statement
\(s:\) If \(x\) is a multiple of \(6\), then \(x\) is a multiple of \(12\).
Identify whether \(s:\) is the inverse, the converse or the contrapositive of \(r\).[1]
Consider the compound statement
\(s:\) If \(x\) is a multiple of \(6\), then \(x\) is a multiple of \(12\).
Determine the validity of \(s\). Justify your decision.[2]
Answer/Explanation
Markscheme
\(x\) is not a multiple of \(12\) (A1) (C1)
\(p \Rightarrow q\) (A1)(A1)(C2)
Note: Award (A1) for \( \Rightarrow \), (A1) for \(p\) and \(q\) in the correct order.
Accept \(q \Leftarrow p\).
Converse (A1) (C1)
not valid (A1)
for example \(18\) is a multiple of \(6\) and not a multiple of \(12\) (R1) (C2)
Notes: Do not award (A1)(R0). Any multiple of 6 that is not a multiple of \(12\) can be accepted as a counterexample.
Question
Consider the following statements
\(z\,:\,x\) is an integer
\(q\,:\,x\) is a rational number
\(r\,:\,x\) is a real number.
i) Write down, in words, \(\neg q\).
ii) Write down a value for \(x\) such that the statement \(\neg q\) is true.[2]
Write the following argument in symbolic form:
“If \(x\) is a real number and \(x\) is not a rational number, then \(x\) is not an integer”.[3]
Phoebe states that the argument in part (b) can be shown to be valid, without the need of a truth table.
Justify Phoebe’s statement.[1]
Answer/Explanation
Markscheme
i) \(x\) is not a rational number (A1)
Note: Accept “\(x\) is an irrational number”.
ii) any non-rational number (for example: \(\pi ,\,\sqrt 2 \), …) (A1) (C2)
\((r \wedge \neg q) \Rightarrow \neg z\) (A1)(A1)(A1) (C3)
Note: Award (A1) for “\( \Rightarrow \)” seen, (A1) for “\(\neg z\)” as the consequent and (A1) for “\((r \wedge \neg q)\)” or “\((\neg q \wedge r)\)” as the antecedent (the parentheses are required).
all integers are rational numbers (and therefore \(x\) cannot be an integer if it is not a rational number) (R1)
Note: Accept equivalent expressions.
OR
if \(x\) is an integer, then \(x\) is a rational number, therefore if \(x\) is not a rational number, then \(x\) is not an integer (contrapositive) (R1) (C1)
Note: Accept “If \(x\) is not in \(\mathbb{Q}\), then \(x\) is not in \(\mathbb{Z}\)” with a Venn diagram showing \(\mathbb{R}\), \(\mathbb{Q}\) and \(\mathbb{Z}\) correctly.
Question
Consider the following propositions:
\(p:\) The lesson is cancelled
\(q:\) The teacher is absent
\(r:\) The students are in the library.
Write, in words, the compound proposition \(q \Rightarrow (p \wedge r).\)[3]
Complete the following truth table.
[2]
Hence, justify why \(q \Rightarrow \neg r\) is not a tautology.[1]
Answer/Explanation
Markscheme
if the teacher is absent then the lesson is cancelled and the students are in the library (A1)(A1)(A1) (C3)
Note: Award (A1) for If…then.
For Spanish candidates, only accept “Si” and “entonces”.
For French candidates, only accept “Si” and “alors”.
For all three languages these words are from the subject guide.
Award (A1) for “and”,
Award (A1) for correct propositions in correct order.
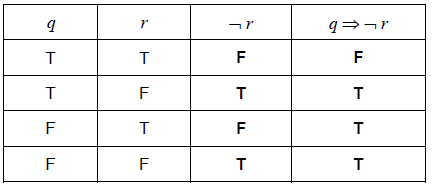
(A1)(A1)(ft) (C2)
Note: Award (A1) for \(\neg r\) column correct and (A1) for \(q \Rightarrow \neg r\) column correct.
Award (A0)(A1)(ft) for a \(q \Rightarrow \neg r\) column that correctly follows from an incorrect \(\neg r\) column.
not all of the entries are true (or equivalent) (R1) (C1)
Note: Accept “One entry is false”.
Question
Consider the following logic propositions.
\(p\): Sandi gets up before eight o’clock
\(q\): Sandi goes for a run
\(r\): Sandi goes for a swim
Write down in words the compound proposition
[3]
Complete the following truth table.
[2]
On a morning when Sandi does not get up before eight o’clock, use your truth table to determine whether \(p \Rightarrow (q{\text{ }}\underline \vee {\text{ }}r)\) is a tautology, contradiction or neither.[1]
Answer/Explanation
Markscheme
If Sandi gets up before eight o’clock then Sandi (either) goes for a run or goes for a swim, but not both. (A1)(A1)(A1) (C3)
Note: Award (A1) for If …… then ……, (A1) for all propositions in the correct order, (A1) for “… or … but not both” (do not accept “either” as a replacement for “but not both”).[3 marks]
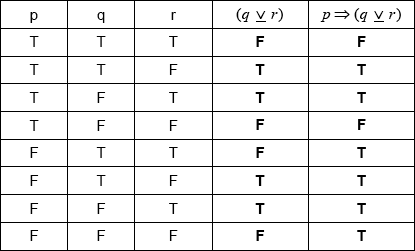(A1)(A1)(ft) (C2)
Note: Award (A1) for correct \((q{\text{ }}\underline \vee {\text{ }}r)\) column, and (A1)(ft) for their correct \(p \Rightarrow (q{\text{ }}\underline \vee {\text{ }}r)\) column. Follow through from their \((q{\text{ }}\underline \vee {\text{ }}r)\) column.[2 marks]
tautology (A1)(ft) (C1)
Note: Follow through from part (b).[1 mark]
Question
Consider the following propositions.
\[\begin{array}{*{20}{l}} {p{\text{: I completed the task}}} \\ {q{\text{: I was paid}}} \end{array}\]
Write down in words \(\neg q\).[1]
Write down in symbolic form the compound statement:
If I was paid then I completed the task.[1]
Complete the following truth table.
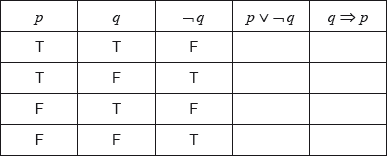[2]
State whether the statements \(p \vee \neg q\) and \(q \Rightarrow p\) are logically equivalent. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
I was not paid (A1) (C1)[1 mark]
\(q \Rightarrow p\) (A1) (C1)[1 mark]
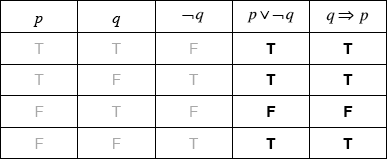(A1)(A1) (C2)
Note: Award (A1) for each correct column.[2 marks]
yes (A1)(ft)
as the last two columns of the truth table are the same (R1)(ft) (C2)
Note: Do not award (A1)(R0). Follow through from part (c)(i).[2 marks]
Question
Consider the following propositions.
\[\begin{array}{*{20}{l}} {p{\text{: The car is under warranty}}} \\ {q{\text{: The car is less than 2 years old}}} \\ {r{\text{ : The car has been driven more than 20}}\,{\text{000 km}}} \end{array}\]
Write down in words \((q \vee \neg r) \Rightarrow p\).[3]
Complete the truth table.
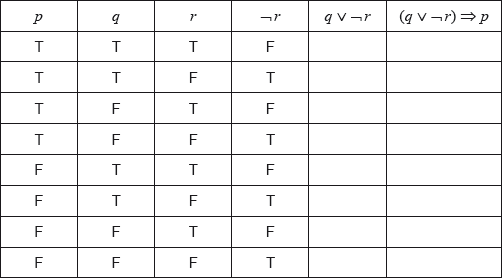[2]
State whether the statement \(\neg p \Rightarrow \neg (q \vee \neg r)\) is the inverse, the converse or the contrapositive of the statement in part (a).[1]
Answer/Explanation
Markscheme
if the car is less than 2 years old or the car has not been driven more than \(20\,000{\text{ km}}\), then the car is under warranty (A1)(A1)(A1) (C3)
Note: Award (A1) for if …, then …, (A1) for “or”, (A1) for correct statements in correct order. Accept “If the car has not been driven more than \(20\,000{\text{ km}}\) or the car is less than 2 years old, then the car is under warranty”. Accept logical equivalent wording for each proposition, eg “less than \(20\,000{\text{ km}}\)”.[3 marks]
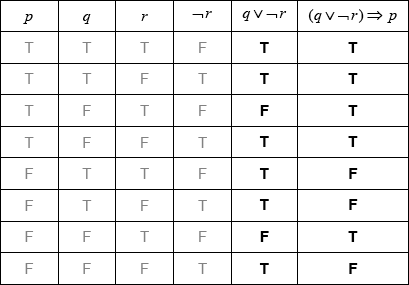(A1)(A1)(ft) (C2)
Note: Award (A1) for \(q \vee \neg r\) column correct and (A1)(ft) for \((q \vee \neg r) \Rightarrow p\) column correct. Follow through from their \(q \vee \neg r\) column.[2 marks]
contrapositive (A1) (C1)[1 mark]
Question
Consider the following propositions.
p: my Mathematical Studies homework is due tomorrow
q: today is Wednesday
Write down in words the compound proposition ¬\(p \Rightarrow q\).[2]
Complete the truth table.
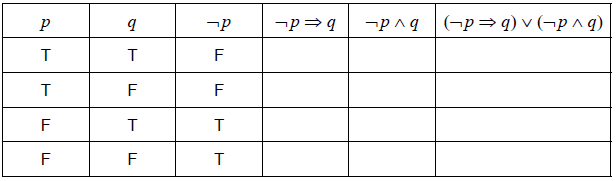[3]
State whether the compound proposition (\(\neg p \Rightarrow q\)) ∨ (\(\neg p \wedge q\)) is a tautology, contradiction or neither.[1]
Answer/Explanation
Markscheme
If my Mathematical Studies homework is not due in tomorrow then today is Wednesday. (A1)(A1) (C2)
Note: Award (A1) for If… then…
Award (A1) for correct propositions, my Mathematical Studies homework is not due in tomorrow and today is Wednesday, in the correct order.
Award (A1)(A0) for “If ¬p then q”.[2 marks]
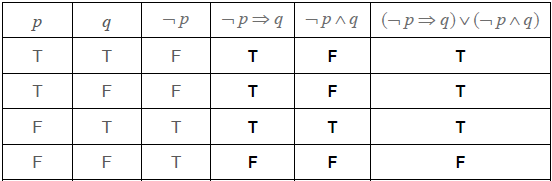(A1)(A1)(A1)(ft) (C3)[3 marks]
neither (A1)(ft) (C1)
Note: Follow through from the final column of their truth table.[1 mark]
Question
Consider the following propositions.
p : the baby cries
q : the baby is happy
r : the baby wants to play
Write down, in words, \(\left( {q \wedge r} \right) \Rightarrow \neg p\).[3]
Complete the following truth table.
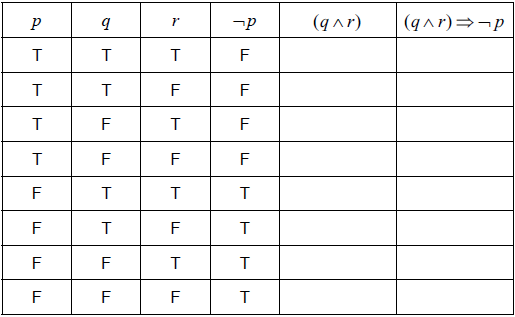[2]
State whether \(\left( {q \wedge r} \right) \Rightarrow \neg p\) is a tautology, contradiction or neither.[1]
Answer/Explanation
Markscheme
if the baby is happy and wants to play then the baby does not cry (A1)(A1)(A1) (C3)
Note: Award (A1) for “If… then…”; (A1) for “the baby is happy and wants to play”, (A1) for “the baby does not cry”. Crying must be negated.[3 marks]
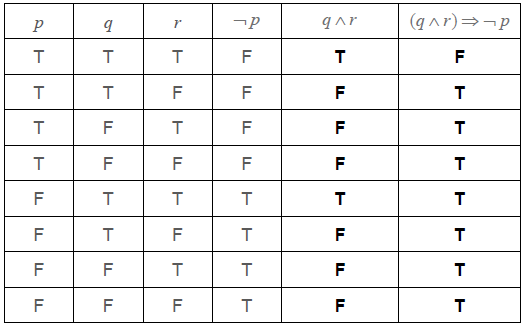(A1)(A1) (C2)
Note: Award (A1) for each correct column.[2 marks]
Neither (A1)(ft) (C1)
Note: Follow through from the last column in their part (b).[1 mark]