Question
The truth table below shows the truth-values for the proposition
\(p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q \Rightarrow \neg {\text{ }}p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } \neg q\)
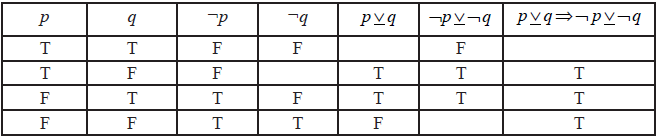
Explain the distinction between the compound propositions, \(p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q\) and \(p \vee q\).[1]
Fill in the four missing truth-values on the table.[4]
State whether the proposition \(p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q \Rightarrow \neg p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } \neg q\) is a tautology, a contradiction or neither.[1]
Answer/Explanation
Markscheme
Both are ‘p or q’, the first is ‘but not both’ (A1)
Note: Award mark for clear understanding if wording is poor. (C1)[1 mark]
 (A1)(A1)(ft)(A1)(A1)
(A1)(A1)(ft)(A1)(A1)
Note: Follow through is for final column. (C4)[4 marks]
Tautology. (A1)(ft) (C1)[1 mark]
Question
B and C are subsets of a universal set U such that
\(U = \left\{ {x:x \in \mathbb{Z},0 \leqslant x < 10} \right\},{\text{ }}B = \left\{ {{\text{prime numbers}} < 10} \right\},{\text{ }}C = \left\{ {x:x \in \mathbb{Z},1 < x \leqslant 6} \right\}.\)
List the members of sets
(i) \(B\)
(ii) \(C \cap B\)
(iii) \(B \cup C′\)[4]
Consider the propositions:
p : x is a prime number less than 10.
q : x is a positive integer between 1 and 7.
Write down, in words, the contrapositive of the statement, “If x is a prime number less than 10, then x is a positive integer between 1 and 7.”[2]
Answer/Explanation
Markscheme
(i) \(B = 2, 3, 5, 7\) (A1)
Brackets not required
(ii) \(C \cap B = 2, 3, 5\) (A1)(ft)
Follow through only from incorrect B
(iii) \(C’ = 0, 1, 7, 8, 9\) (A1)(ft)
\(B \cup C’ = 0, 1, 2, 3, 5, 7, 8, 9\) (A1)(ft)
Note: Award (A1) for correct \(C’\) seen. The first (A1)(ft) in (iii) can be awarded only if C was listed incorrectly and a mark was lost as a result in (a)(ii). If C was not listed and \(C’\) is wrong, the first mark is lost. The second mark can (ft) within part (iii) as well as from (i). (C4)[4 marks]
“If x is not a positive integer between 1 and 7, then x is not a prime number less than 10.” (A1)(A1)
Award (A1) for both (not) statements, (A1) for correct order. (C2)[2 marks]
Question
You may choose from three courses on a lunchtime menu at a restaurant.
s: you choose a salad,
m: you choose a meat dish (main course),
d: you choose a dessert.
You choose a two course meal which must include a main course and either a salad or a dessert, but not both.
Write the sentence above using logic symbols.[2]
Write in words \(s \Rightarrow \neg d\) .[2]
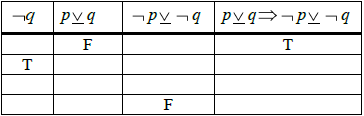
Complete the following truth table.
 [2]
[2]
Answer/Explanation
Markscheme
\(m \wedge (s \underline{\vee} d)\) (A2)
(A1) for \(m \wedge \)
(A1) for \((s\underline{ \vee } d)\)
(A1)(A0) if brackets are missing.
OR
\((m \wedge s) \underline{\vee} (m \wedge d)\) (A2)
(A1) for both brackets correct, (A1) for disjunctive “or” (A1)(A0) if brackets are missing. (C2)[2 marks]
If you choose a salad then you do not choose a dessert. (A2)
(A1) for “if …then…” (A1) for salad and no dessert in the correct order.
OR
If you choose a salad you do not choose a dessert. (A2) (C2)[2 marks]
(A1) for each correct column (A1)(A1)(ft) (C2)[2 marks]
Question
Consider the following logic propositions:
\(p:{\text{ Sean is at school}}\)
\(q:{\text{ Sean is playing a game on his computer}}{\text{.}}\)
Write in words, \(p \underline { \vee } q\).[2]
Write in words, the converse of \(p \Rightarrow \neg q\).[2]
Complete the following truth table for \(p \Rightarrow \neg q\).
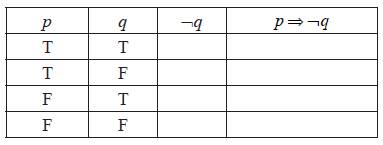 [2]
[2]
Answer/Explanation
Markscheme
Either Sean is at school or Sean is playing a game on his computer but not both. (A1)(A1) (C2)
Note: (A1) for ‘either … or but not both’ (A1) for correct statements. ‘Either’ can be omitted.[2 marks]
If Sean is not playing a game on his computer then Sean is at school. (A1)(A1) (C2)
Note: (A1) for ‘If … then’ (A1) for correct propositions in the correct order.[2 marks]
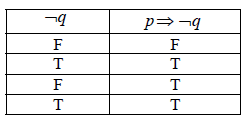 (A1)(A1)(ft) (C2)
(A1)(A1)(ft) (C2)
Note: (A1) for each correct column.[2 marks]
Question
(i) Complete the truth table below.
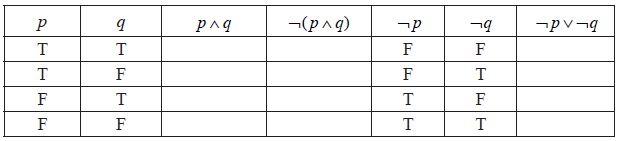
(ii) State whether the compound propositions \(\neg (p \wedge q)\) and \(\neg p \vee \neg q\) are equivalent.[4]
Consider the following propositions.
\(p:{\text{ Amy eats sweets}}\)
\(q:{\text{ Amy goes swimming.}}\)
Write, in symbolic form, the following proposition.
Amy either eats sweets or goes swimming, but not both.[2]
Answer/Explanation
Markscheme
(i)
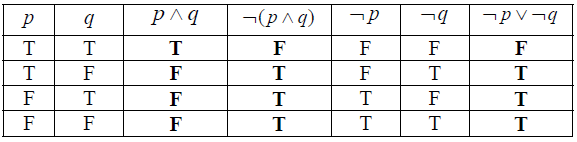 (A3)
(A3)
Note: Award (A1) for \(p \wedge q\) column correct, (A1)(ft) for \(\neg (p \wedge q)\) column correct, (A1) for last column correct.
(ii) Yes. (R1)(ft) (C4)
Note: (ft) from their second and the last columns. Must be correct from their table.[4 marks]
\(p {\underline \vee} q\). (A1)(A1) (C2)
Note: Award (A1) for \(p \ldots q\), (A1) for \({\underline \vee} \). Accept \((p \vee q) \wedge \neg (p \wedge q)\) or \((p \vee q) \wedge (\neg p \vee \neg q)\).[2 marks]
Question
Let \(p\) and \(q\) represent the propositions
\(p\): food may be taken into the cinema
\(q\): drinks may be taken into the cinema
Complete the truth table below for the symbolic statement \(\neg (p \vee q)\) .
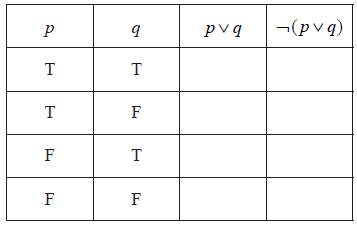 [2]
[2]
Write down in words the meaning of the symbolic statement \(\neg (p \vee q)\).[2]
Write in symbolic form the compound statement:
“no food and no drinks may be taken into the cinema”.[2]
Answer/Explanation
Markscheme
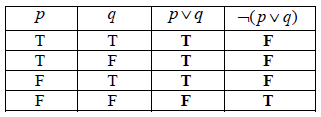 (A1)(A1)(ft) (C2)
(A1)(A1)(ft) (C2)
Note: (A1) for each correct column.[2 marks]
It is not true that food or drinks may be taken into the cinema.
Note: (A1) for “it is not true”. (A1) for “food or drinks”.
OR
Neither food nor drinks may be taken into the cinema.
Note: (A1) for “neither”. (A1) for “nor”.
OR
No food and no drinks may be taken into the cinema.
Note: (A1) for “no food”, “no drinks”. (A1) for “and”.
OR
No food or drink may be brought into the cinema. (A2) (C2)
Note: (A1) for “no”, (A1) for “food or drink”. Do not penalize for use of plural/singular.
Note: the following answers are incorrect:
No food and drink may be brought into the cinema. Award (A1) (A0)
Food and drink may not be brought into the cinema. Award (A1) (A0)
No food or no drink may be brought into the cinema. Award (A1) (A0)[2 marks]
\(\neg p \wedge \neg q\)
Note: (A1) for both negations, (A1) for conjunction.
OR
\(\neg (p \vee q)\) (A1)(A1) (C2)
Note: (A1) for negation, (A1) for \(p \vee q\) in parentheses.[2 marks]
Question
Consider the two propositions p and q.
p: The sun is shining q: I will go swimming
Write in words the compound proposition
\(p \Rightarrow q\) ;[2]
Write in words the compound proposition
\(\neg p \vee q\).[2]
The truth table for these compound propositions is given below.

Complete the column for \( \neg p\).[1]
The truth table for these compound propositions is given below.

State the relationship between the compound propositions \(p \Rightarrow q\) and \(\neg p \vee q\) .[1]
Answer/Explanation
Markscheme
If the sun is shining then I will go swimming. (A1)(A1) (C2)
Note: Award (A1) for “if…then” and (A1) for correct order.[2 marks]
Either the sun is not shining or I will go swimming. (A1)(A1) (C2)
Note: Award (A1) for both correct statements and (A1) for “either” “…or”.[2 marks]
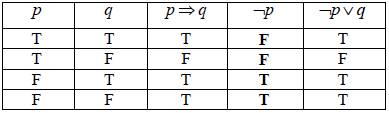 (A1) (C1)[1 mark]
(A1) (C1)[1 mark]
They are (logically) equivalent. (A1) (C1)
Note: Do not accept any other answers.[1 mark]
Question
Consider two propositions p and q.
Complete the truth table below.
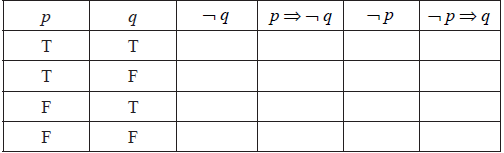 [4]
[4]
Decide whether the compound proposition
\[\left( {{\text{ }}p \Rightarrow \neg q} \right) \Leftrightarrow \left( {\neg p \Rightarrow q} \right)\]
is a tautology. State the reason for your decision.[2]
Answer/Explanation
Markscheme
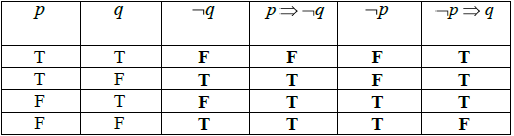 (A1)(A1)(ft)(A1)(A1)(ft) (C4)
(A1)(A1)(ft)(A1)(A1)(ft) (C4)
Note: Award (A1) for each correct column (second column (ft) from first, fourth (ft) from third). Follow through from second column to fourth column for a consistent mistake in implication.[4 marks]
Since second and fourth columns are not identical (R1)(ft)
\( \Rightarrow \) Not a tautology (A1)(ft) (C2)
Note: (R0)(A1) may not be awarded.[2 marks]
Question
Complete the truth table below.
 [4]
[4]
State whether the statement \((p \wedge q) \Rightarrow (\neg p \underline \vee q)\) is a logical contradiction, a tautology or neither.[1]
Give a reason for your answer to part (b)(i).[1]
Answer/Explanation
Markscheme
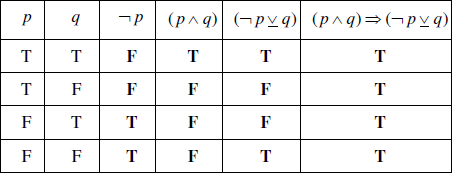 (A1)(A1)(A1)(ft)(A1)(ft) (C4)
(A1)(A1)(A1)(ft)(A1)(ft) (C4)
Notes: Award (A1) for each correct column.
Award first (A1)(ft) from their third column in the table.
Award second (A1)(ft) from their fourth and fifth column in the table.[4 marks]
Tautology (A1)(ft) (C1)
Note: Answer must be consistent with last column in table.[1 mark]
All entries (in the final column) are true. (R1)(ft) (C1)
Note: Answer must be consistent with their answer to part (b)(i).
Note: Special case (A1)(R0) may be awarded.[1 mark]
Question
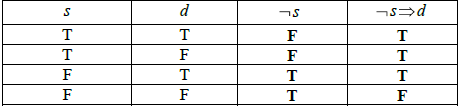
Consider the statement \(p \Rightarrow q\).
If I break my arm, then it will hurt.
Write down in words, the inverse of \(p \Rightarrow q\).[2]
Complete the following truth table.
 [2]
[2]
State whether the converse and the inverse of an implication are logically equivalent.
Justify your answer.[2]
Answer/Explanation
Markscheme
If I do not break my arm, then it will not hurt (A1)(A1) (C2)
Note: Award (A1) for “if… then…”
For Spanish candidates, only accept “Si” and “entonces”.
Award (A1) for “not break my arm” and “not hurt” in correct order.

(A1)(A1) (C2)
Notes: Award (A1) for each correct column.
logically equivalent (A1)(ft)
last two columns of the truth table are identical (R1)(ft) (C2)
Notes: Do not award (A1)(ft)(R0).
Follow through from the last two columns of the table in part (a).
Question
Consider the propositions \(r\), \(p\) and \(q\).
Complete the following truth table.
 [4]
[4]
Determine whether the compound proposition \(\neg \left( {(r \wedge p) \vee \neg q)} \right) \Leftrightarrow \neg (r \wedge p) \wedge q\) is a tautology, a contradiction or neither.
Give a reason.[2]
Answer/Explanation
Markscheme
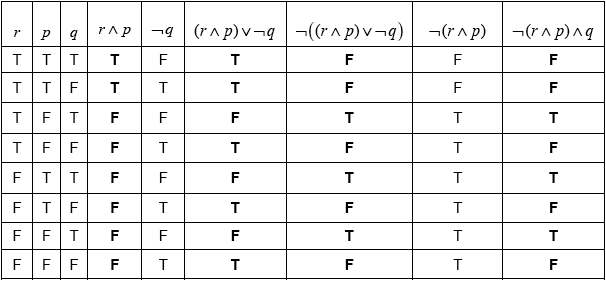 (A1)(A1)(ft)(A1)(ft)(A1) (C4)
(A1)(A1)(ft)(A1)(ft)(A1) (C4)
Notes: Award (A1) for each correct column.
For the “\({(r \wedge p) \vee \neg q}\)” follow through from the “\(r \wedge p\)” column.
For the “\(\neg \left( {(r \wedge p) \vee \neg q)} \right)\)” column, follow through from the preceding column.
tautology (A1)(ft)
columns \(\neg \left( {(r \wedge p) \vee \neg q)} \right)\) and \(\neg (r \wedge p) \wedge q\) are identical (R1)(C2)
Notes: Do not award (R0)(A1)(ft). Follow through from their table in part (a).
Award the (R1) for an additional column representing \(\neg \left( {(r \wedge p) \vee \neg q)} \right) \Leftrightarrow \neg (r \wedge p) \wedge q\) that is consistent with their table.
Question
\(p:x\) is a multiple of \(12\)
\(q:x\) is a multiple of \(6\).
Write down in words \(\neg p\).[1]
Write down in symbolic form the compound statement
\(r:\) If \(x\) is a multiple of \(12\), then \(x\) is a multiple of \(6\).[2]
Consider the compound statement
\(s:\) If \(x\) is a multiple of \(6\), then \(x\) is a multiple of \(12\).
Identify whether \(s:\) is the inverse, the converse or the contrapositive of \(r\).[1]
Consider the compound statement
\(s:\) If \(x\) is a multiple of \(6\), then \(x\) is a multiple of \(12\).
Determine the validity of \(s\). Justify your decision.[2]
Answer/Explanation
Markscheme
\(x\) is not a multiple of \(12\) (A1) (C1)
\(p \Rightarrow q\) (A1)(A1)(C2)
Note: Award (A1) for \( \Rightarrow \), (A1) for \(p\) and \(q\) in the correct order.
Accept \(q \Leftarrow p\).
Converse (A1) (C1)
not valid (A1)
for example \(18\) is a multiple of \(6\) and not a multiple of \(12\) (R1) (C2)
Notes: Do not award (A1)(R0). Any multiple of 6 that is not a multiple of \(12\) can be accepted as a counterexample.
Question
Consider the following propositions.
\[\begin{array}{*{20}{l}} {p{\text{: The car is under warranty}}} \\ {q{\text{: The car is less than 2 years old}}} \\ {r{\text{ : The car has been driven more than 20}}\,{\text{000 km}}} \end{array}\]
Write down in words \((q \vee \neg r) \Rightarrow p\).[3]
Complete the truth table.
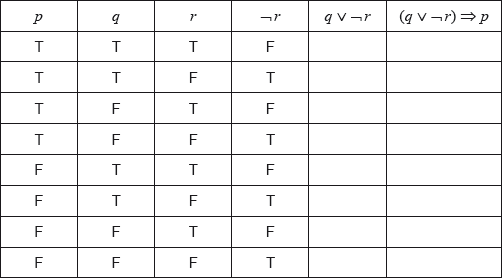 [2]
[2]
State whether the statement \(\neg p \Rightarrow \neg (q \vee \neg r)\) is the inverse, the converse or the contrapositive of the statement in part (a).[1]
Answer/Explanation
Markscheme
if the car is less than 2 years old or the car has not been driven more than \(20\,000{\text{ km}}\), then the car is under warranty (A1)(A1)(A1) (C3)
Note: Award (A1) for if …, then …, (A1) for “or”, (A1) for correct statements in correct order. Accept “If the car has not been driven more than \(20\,000{\text{ km}}\) or the car is less than 2 years old, then the car is under warranty”. Accept logical equivalent wording for each proposition, eg “less than \(20\,000{\text{ km}}\)”.[3 marks]
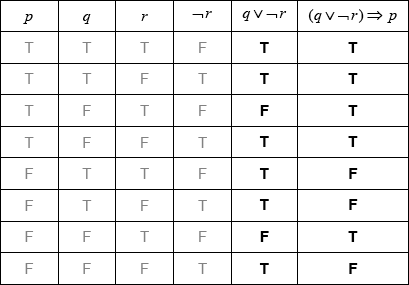 (A1)(A1)(ft) (C2)
(A1)(A1)(ft) (C2)
Note: Award (A1) for \(q \vee \neg r\) column correct and (A1)(ft) for \((q \vee \neg r) \Rightarrow p\) column correct. Follow through from their \(q \vee \neg r\) column.[2 marks]
contrapositive (A1) (C1)[1 mark]
Question
Consider the following propositions.
p : the baby cries
q : the baby is happy
r : the baby wants to play
Write down, in words, \(\left( {q \wedge r} \right) \Rightarrow \neg p\).[3]
Complete the following truth table.
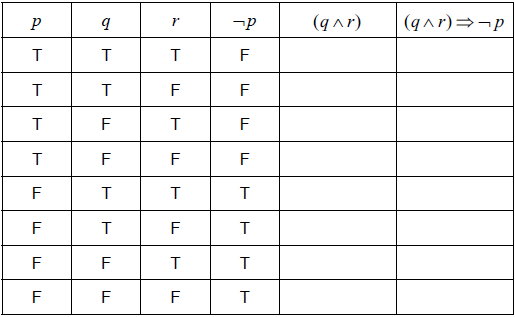 [2]
[2]
State whether \(\left( {q \wedge r} \right) \Rightarrow \neg p\) is a tautology, contradiction or neither.[1]
Answer/Explanation
Markscheme
if the baby is happy and wants to play then the baby does not cry (A1)(A1)(A1) (C3)
Note: Award (A1) for “If… then…”; (A1) for “the baby is happy and wants to play”, (A1) for “the baby does not cry”. Crying must be negated.[3 marks]
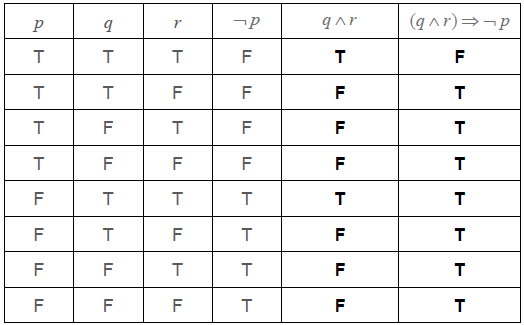 (A1)(A1) (C2)
(A1)(A1) (C2)
Note: Award (A1) for each correct column.[2 marks]
Neither (A1)(ft) (C1)
Note: Follow through from the last column in their part (b).[1 mark]
Question
Consider the following statements about the quadrilateral ABCD
\(q:\) ABCD has four equal sides \(s:\) ABCD is a square
Express in words the statement, \(s \Rightarrow q\) .[2]
Write down in words, the inverse of the statement, \(s \Rightarrow q\) .[2]
Determine the validity of the argument in (b). Give a reason for your decision.[2]
Answer/Explanation
Markscheme
If ABCD is a square, then ABCD has four equal sides. (A1)(A1) (C2)
Note: Award (A1) for if… then, (A1) for propositions in the correct order.
If ABCD is not a square, then ABCD does not have four equal sides. (A1)(A1) (C2)
Note: Award (A1) for if… then, (A1) for propositions in the correct order.
Not a valid argument. ABCD may have 4 equal sides but will not necessarily be a square. (It may be a rhombus) (A1)(R1) (C2)
Note: Award (R1) for correct reasoning, award (A1) for a consistent conclusion with their answer in part (b).
It is therefore possible that (R1)(A0) may be awarded, but (R0)(A1) can never be awarded.
Note: Simple examples of determining the validity of an argument without the use of a truth table may be tested.

