Download IITian Academy App for accessing Online Mock Tests and More..
Question
(i) Complete the truth table below.
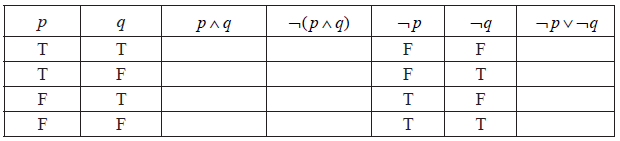
(ii) State whether the compound propositions \(\neg (p \wedge q)\) and \(\neg p \vee \neg q\) are equivalent.[4]
Consider the following propositions.
\(p:{\text{ Amy eats sweets}}\)
\(q:{\text{ Amy goes swimming.}}\)
Write, in symbolic form, the following proposition.
Amy either eats sweets or goes swimming, but not both.[2]
Answer/Explanation
Markscheme
(i)
(A3)
Note: Award (A1) for \(p \wedge q\) column correct, (A1)(ft) for \(\neg (p \wedge q)\) column correct, (A1) for last column correct.
(ii) Yes. (R1)(ft) (C4)
Note: (ft) from their second and the last columns. Must be correct from their table.[4 marks]
\(p {\underline \vee} q\). (A1)(A1) (C2)
Note: Award (A1) for \(p \ldots q\), (A1) for \({\underline \vee} \). Accept \((p \vee q) \wedge \neg (p \wedge q)\) or \((p \vee q) \wedge (\neg p \vee \neg q)\).[2 marks]
Question
Consider the two propositions p and q.
p: The sun is shining q: I will go swimming
Write in words the compound proposition
\(p \Rightarrow q\) ;[2]
Write in words the compound proposition
\(\neg p \vee q\).[2]
The truth table for these compound propositions is given below.
Complete the column for \( \neg p\).[1]
The truth table for these compound propositions is given below.
State the relationship between the compound propositions \(p \Rightarrow q\) and \(\neg p \vee q\) .[1]
Answer/Explanation
Markscheme
If the sun is shining then I will go swimming. (A1)(A1) (C2)
Note: Award (A1) for “if…then” and (A1) for correct order.[2 marks]
Either the sun is not shining or I will go swimming. (A1)(A1) (C2)
Note: Award (A1) for both correct statements and (A1) for “either” “…or”.[2 marks]
(A1) (C1)[1 mark]
They are (logically) equivalent. (A1) (C1)
Note: Do not accept any other answers.[1 mark]
Question
Consider the statement p:
“If a quadrilateral is a square then the four sides of the quadrilateral are equal”.
Write down the inverse of statement p in words.[2]
Write down the converse of statement p in words.[2]
Determine whether the converse of statement p is always true. Give an example to justify your answer.[2]
Answer/Explanation
Markscheme
If a quadrilateral is not a square (then) the four sides of the quadrilateral are not equal. (A1)(A1) (C2)
Note: Award (A1) for “if…(then)”, (A1) for the correct phrases in the correct order.[2 marks]
If the four sides of the quadrilateral are equal (then) the quadrilateral is a square. (A1)(A1)(ft) (C2)
Note: Award (A1) for “if…(then)”, (A1)(ft) for the correct phrases in the correct order.
Note: Follow through in (b) if the inverse and converse in (a) and (b) are correct and reversed.[2 marks]
The converse is not always true, for example a rhombus (diamond) is a quadrilateral with four equal sides, but it is not a square. (A1)(R1) (C2)
Note: Do not award (A1)(R0).[2 marks]
Question
Complete the following truth table.
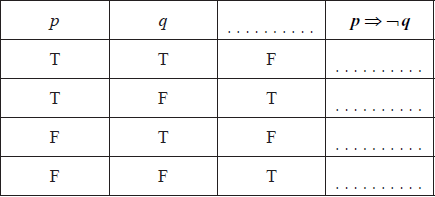[2]
Consider the propositions
p: Cristina understands logic
q: Cristina will do well on the logic test.
Write down the following compound proposition in symbolic form.
“If Cristina understands logic then she will do well on the logic test”[2]
Write down in words the contrapositive of the proposition given in part (b).[2]
Answer/Explanation
Markscheme
(A1)(A1) (C2)
Note: Award (A1) for ¬q , (A1) for last column.[2 marks]
\(p \Rightarrow q\) (A1)(A1) (C2)
Note: Award (A1) for \(\Rightarrow\) , (A1) for p and q in the correct order.[2 marks]
If Cristina does not do well on the logic test then she does not understand logic. (A1)(A1) (C2)
Note: Award (A1) for If…(then), must be an implication, (A1) for the correct propositions in the correct order.[2 marks]
Question
Consider the statements
p : The numbers x and y are both even.
q : The sum of x and y is an even number.
Write down, in words, the statement p \(\Rightarrow\) q.[2]
Write down, in words, the inverse of the statement p \(\Rightarrow\) q.[2]
State whether the inverse of the statement p \( \Rightarrow \) q is always true. Justify your answer.[2]
Answer/Explanation
Markscheme
If (both) the numbers x and y are even (then) the sum of x and y is an even number. (A1)(A1) (C2)
Note: Award (A1) for If…(then), (A1) for the correct statements in the correct order.[2 marks]
If (both) the numbers x and y are not even (then) the sum of x and y is not an even number. (A1)(A1) (C2)
Notes: Award (A1) for If…(then), (A1) for the correct not p, and not q in the correct order. Accept the word odd for the phrase “not even”.[2 marks]
The inverse of a statement is not (necessarily) true, because two odd (not even) numbers, always have an even sum. (A1)(R1)(ft) (C2)
Notes: Award (A1)(R1) if a specific counter example given instead of a reason stated in general terms, e.g. the inverse is not true because, 5 and 7 have an even sum. Do not award (A1)(R0). Follow through from their statement in part (b).[2 marks]
Question
Consider the following logic statements.
p: Carlos is playing the guitar
q: Carlos is studying for his IB exams
Write in words the compound statement \(\neg p \wedge q\) .[2]
Write the following statement in symbolic form.
“Either Carlos is playing the guitar or he is studying for his IB exams but not both.”[1]
Write the converse of the following statement in symbolic form.
“If Carlos is playing the guitar then he is not studying for his IB exams.”[3]
Answer/Explanation
Markscheme
Carlos is not playing the guitar and he is studying for his IB exams. (A1)(A1) (C2)
Note: Award (A1) for “and”, (A1) for correct statements.[2 marks]
\(p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q\) (A1) (C1)[1 mark]
\(\neg q \Rightarrow p\) (A1)(A1)(A1) (C3)
Notes: Award (A1) for implication, (A1) for the \(\neg q\), (A1) for both \(\neg q\) and \(p\) in the correct order. If correct converse seen in words only award (A1)(A1)(A0). Accept \(p \Leftarrow \neg q\). Accept \( – q\) for \(\neg q\).[3 marks]
Question
Consider the following logic propositions:
p : Yuiko is studying French.
q : Yuiko is studying Chinese.
Write down the following compound propositions in symbolic form.
(i) Yuiko is studying French but not Chinese.
(ii) Yuiko is studying French or Chinese, but not both.[3]
Write down in words the inverse of the following compound proposition.
If Yuiko is studying Chinese, then she is not studying French.[3]
Answer/Explanation
Markscheme
(i) \(p \wedge \neg q\) (A1)(A1)
Note: Award (A1) for conjunction, (A1) for negation of q.
(ii) \(p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q\) OR \((p \vee q)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } (p \wedge q)\) (A1) (C3)
If Yuiko is not studying Chinese, (then) she is studying French. (A1)(A1)(A1) (C3)
Notes: Award (A1) for “if … (then)” seen, award (A1) for “not studying Chinese” seen, (A1) for correct propositions in correct order.
Question
Complete the truth table.
[2]
Consider the propositions p and q:
p: x is a number less than 10.
q: x2 is a number greater than 100.
Write in words the compound proposition \(\neg p \vee q\).[2]
Using part (a), determine whether \(\neg p \vee q\) is true or false, for the case where \(x\) is a number less than 10 and \(x^2\) is a number greater than 100.[1]
Write down a value of \(x\) for which \(\neg p \vee q\) is false.[1]
Answer/Explanation
Markscheme
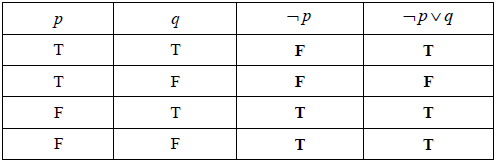
(A1) for third column and (A1)(ft) for fourth column (A1)(A1)(ft) (C2)
\(x\) is greater than or equal to (not less than) 10 or \(x^2\) is greater than 100. (A1)(A1) (C2)
Note: Award (A1) for “greater than or equal to (not less than) 10”, (A1) for “or \(x^2\) is greater than 100”.
True (A1)(ft) (C1)
Note: Follow through from their answer to part (a).
Any value of \(x\) such that \( – 10 \leqslant x < 10\). (A1)(ft) (C1)
Note: Follow through from their answer to part (a).
Question
Consider the propositions
\(p\): I have a bowl of soup.
\(q\): I have an ice cream.
Write down, in words, the compound proposition \(\neg p \Rightarrow q\).[2]
Complete the truth table.
[2]
Write down, in symbolic form, the converse of \(\neg p \Rightarrow q\).[2]
Answer/Explanation
Markscheme
If I do not have a bowl of soup then I have an ice cream. (A1)(A1) (C2)
Notes: Award (A1) for If… then…
Award (A1) for correct statements in correct order.[2 marks]
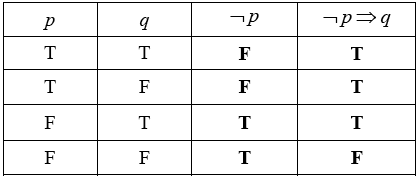(A1)(A1)(ft) (C2)
Note: Follow through from third column to fourth column.[2 marks]
\(q \Rightarrow \neg p\) (A1)(A1) (C2)
Notes: Award (A1) for \( \Rightarrow \).
Award (A1) for \(q\) and \(\neg p\) in correct order.
Accept \(\neg p \Leftarrow q\).[2 marks]
Question
Two propositions are defined as follows:
\(p:\) Quadrilateral ABCD has two diagonals that are equal in length.
\(q:\) Quadrilateral ABCD is a rectangle.
Express the following in symbolic form.
“A rectangle always has two diagonals that are equal in length.”[2]
Write down in symbolic form the converse of the statement in (a).[1]
Determine, without using a truth table, whether the statements in (a) and (b) are logically equivalent.[2]
Write down the name of the statement that is logically equivalent to the converse.[1]
Answer/Explanation
Markscheme
\(q \Rightarrow p\) (A1)(A1) (C2)
Note: Award the first (A1) for seeing the implication sign, the second (A1) is for a correct answer only. Not using the implication earns no marks.[2 marks]
\(p \Rightarrow q\) (A1)(ft) (C1)
Note: Award (A1)(ft) where the propositions in the implication in part (a) are exchanged.[1 mark]
Not equivalent; a kite or an isosceles trapezium (for example) can have diagonals that are equal in length. (A1)(R1) (C2)
Notes: Accept a valid sketch as reasoning.
If the reason given is that a square has diagonals of equal length, but is not a rectangle, then award (R1)(A0).
Do not award (A1)(R0).
Do not accept solutions based on truth tables.[2 marks]
Inverse (A1) (C1)
Note: Do not accept symbolic notation.[1 mark]
Question
Two propositions \(p\) and \(q\) are defined as follows
\(p\): Eva is on a diet
\(q\): Eva is losing weight.
Write down the following statement in words.
\[q \Rightarrow p\][2]
Write down, in words, the contrapositive statement of \(q \Rightarrow p\).[2]
Determine whether your statement in part (a) is logically equivalent to your statement in part (b). Justify your answer.[2]
Answer/Explanation
Markscheme
If Eva is losing weight then Eva is on a diet (A1)(A1) (C2)
Notes: Award (A1) for If… then…
For Spanish candidates, only accept “Si” and “entonces”.
For French candidates, only accept “Si” and “alors”.
For all 3 languages these words are from the subject guide.
Award (A1) for correct propositions in correct order.[2 marks]
If Eva is not on a diet then she is not losing weight (A1)(A1) (C2)
Notes: Award (A1) for “not on a diet” and “not losing weight” seen, (A1) for complete correct answer.
No follow through from part (a).[2 marks]
The statements are logically equivalent (A1)(ft)
The contrapositive is always logically equivalent to the original statement (R1)(ft)
OR
A correct truth table showing the equivalence (R1)(ft) (C2)
Note: Follow through from their answers to part (a) and part (b).[2 marks]
Question
Consider the statement \(p \Rightarrow q\).
If I break my arm, then it will hurt.
Write down in words, the inverse of \(p \Rightarrow q\).[2]
Complete the following truth table.
[2]
State whether the converse and the inverse of an implication are logically equivalent.
Justify your answer.[2]
Answer/Explanation
Markscheme
If I do not break my arm, then it will not hurt (A1)(A1) (C2)
Note: Award (A1) for “if… then…”
For Spanish candidates, only accept “Si” and “entonces”.
Award (A1) for “not break my arm” and “not hurt” in correct order.
(A1)(A1) (C2)
Notes: Award (A1) for each correct column.
logically equivalent (A1)(ft)
last two columns of the truth table are identical (R1)(ft) (C2)
Notes: Do not award (A1)(ft)(R0).
Follow through from the last two columns of the table in part (a).
Question
\(p:x\) is a multiple of \(12\)
\(q:x\) is a multiple of \(6\).
Write down in words \(\neg p\).[1]
Write down in symbolic form the compound statement
\(r:\) If \(x\) is a multiple of \(12\), then \(x\) is a multiple of \(6\).[2]
Consider the compound statement
\(s:\) If \(x\) is a multiple of \(6\), then \(x\) is a multiple of \(12\).
Identify whether \(s:\) is the inverse, the converse or the contrapositive of \(r\).[1]
Consider the compound statement
\(s:\) If \(x\) is a multiple of \(6\), then \(x\) is a multiple of \(12\).
Determine the validity of \(s\). Justify your decision.[2]
Answer/Explanation
Markscheme
\(x\) is not a multiple of \(12\) (A1) (C1)
\(p \Rightarrow q\) (A1)(A1)(C2)
Note: Award (A1) for \( \Rightarrow \), (A1) for \(p\) and \(q\) in the correct order.
Accept \(q \Leftarrow p\).
Converse (A1) (C1)
not valid (A1)
for example \(18\) is a multiple of \(6\) and not a multiple of \(12\) (R1) (C2)
Notes: Do not award (A1)(R0). Any multiple of 6 that is not a multiple of \(12\) can be accepted as a counterexample.
Question
Consider the following logic propositions.
\(p\): Sandi gets up before eight o’clock
\(q\): Sandi goes for a run
\(r\): Sandi goes for a swim
Write down in words the compound proposition
[3]
Complete the following truth table.
[2]
On a morning when Sandi does not get up before eight o’clock, use your truth table to determine whether \(p \Rightarrow (q{\text{ }}\underline \vee {\text{ }}r)\) is a tautology, contradiction or neither.[1]
Answer/Explanation
Markscheme
If Sandi gets up before eight o’clock then Sandi (either) goes for a run or goes for a swim, but not both. (A1)(A1)(A1) (C3)
Note: Award (A1) for If …… then ……, (A1) for all propositions in the correct order, (A1) for “… or … but not both” (do not accept “either” as a replacement for “but not both”).[3 marks]
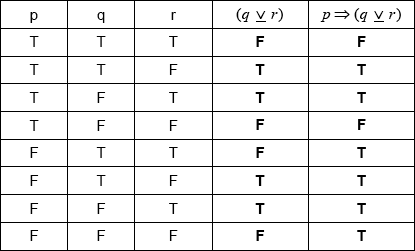(A1)(A1)(ft) (C2)
Note: Award (A1) for correct \((q{\text{ }}\underline \vee {\text{ }}r)\) column, and (A1)(ft) for their correct \(p \Rightarrow (q{\text{ }}\underline \vee {\text{ }}r)\) column. Follow through from their \((q{\text{ }}\underline \vee {\text{ }}r)\) column.[2 marks]
tautology (A1)(ft) (C1)
Note: Follow through from part (b).[1 mark]
Question
Consider the following propositions.
\[\begin{array}{*{20}{l}} {p{\text{: I completed the task}}} \\ {q{\text{: I was paid}}} \end{array}\]
Write down in words \(\neg q\).[1]
Write down in symbolic form the compound statement:
If I was paid then I completed the task.[1]
Complete the following truth table.
[2]
State whether the statements \(p \vee \neg q\) and \(q \Rightarrow p\) are logically equivalent. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
I was not paid (A1) (C1)[1 mark]
\(q \Rightarrow p\) (A1) (C1)[1 mark]
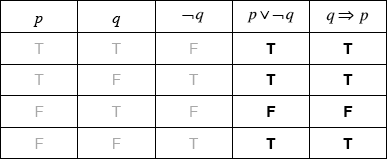(A1)(A1) (C2)
Note: Award (A1) for each correct column.[2 marks]
yes (A1)(ft)
as the last two columns of the truth table are the same (R1)(ft) (C2)
Note: Do not award (A1)(R0). Follow through from part (c)(i).[2 marks]
Question
Consider the following propositions.
\[\begin{array}{*{20}{l}} {p{\text{: The car is under warranty}}} \\ {q{\text{: The car is less than 2 years old}}} \\ {r{\text{ : The car has been driven more than 20}}\,{\text{000 km}}} \end{array}\]
Write down in words \((q \vee \neg r) \Rightarrow p\).[3]
Complete the truth table.
[2]
State whether the statement \(\neg p \Rightarrow \neg (q \vee \neg r)\) is the inverse, the converse or the contrapositive of the statement in part (a).[1]
Answer/Explanation
Markscheme
if the car is less than 2 years old or the car has not been driven more than \(20\,000{\text{ km}}\), then the car is under warranty (A1)(A1)(A1) (C3)
Note: Award (A1) for if …, then …, (A1) for “or”, (A1) for correct statements in correct order. Accept “If the car has not been driven more than \(20\,000{\text{ km}}\) or the car is less than 2 years old, then the car is under warranty”. Accept logical equivalent wording for each proposition, eg “less than \(20\,000{\text{ km}}\)”.[3 marks]
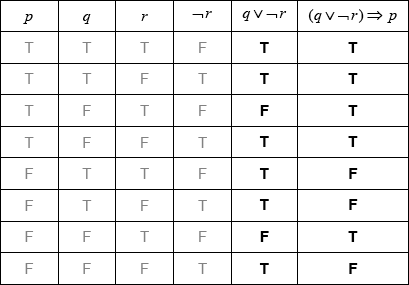(A1)(A1)(ft) (C2)
Note: Award (A1) for \(q \vee \neg r\) column correct and (A1)(ft) for \((q \vee \neg r) \Rightarrow p\) column correct. Follow through from their \(q \vee \neg r\) column.[2 marks]
contrapositive (A1) (C1)[1 mark]
Question
Consider each of the following statements
\[p:Alex{\text{ }}is{\text{ }}from{\text{ }}Uruguay\]\[q:Alex{\text{ }}is{\text{ }}a{\text{ }}scientist\]\[r:Alex{\text{ }}plays{\text{ }}the{\text{ }}flute\]
Write the following argument in words
\[\neg r \Rightarrow (q \vee p)\][3]
Complete the truth table for the argument in part (a) using the values below for \(p\) , \(q\) , \(r\) and \(\neg r\).
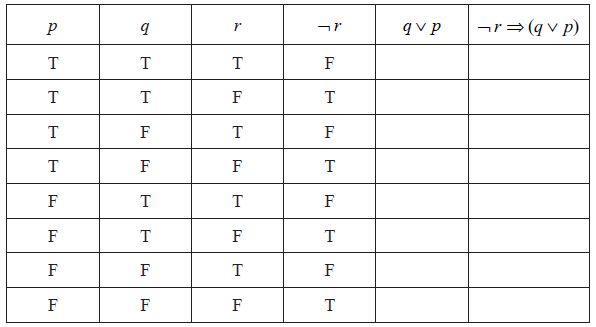[2]
The argument \(\neg r \Rightarrow (q \vee p)\) is invalid. State the reason for this.[1]
Answer/Explanation
Markscheme
If Alex does not play the flute then he is either a scientist or from Uruguay. (A1)(A1)(A1) (C3)
Note: Award (A1) if… then, correct (A1) antecedent, (A1) correct consequent.
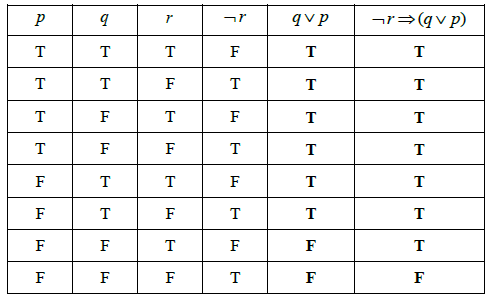(A1)(A1) (C2)
Not all entries in the final column are T. (R1) (C1)
Question
Consider the following statements about the quadrilateral ABCD
\(q:\) ABCD has four equal sides \(s:\) ABCD is a square
Express in words the statement, \(s \Rightarrow q\) .[2]
Write down in words, the inverse of the statement, \(s \Rightarrow q\) .[2]
Determine the validity of the argument in (b). Give a reason for your decision.[2]
Answer/Explanation
Markscheme
If ABCD is a square, then ABCD has four equal sides. (A1)(A1) (C2)
Note: Award (A1) for if… then, (A1) for propositions in the correct order.
If ABCD is not a square, then ABCD does not have four equal sides. (A1)(A1) (C2)
Note: Award (A1) for if… then, (A1) for propositions in the correct order.
Not a valid argument. ABCD may have 4 equal sides but will not necessarily be a square. (It may be a rhombus) (A1)(R1) (C2)
Note: Award (R1) for correct reasoning, award (A1) for a consistent conclusion with their answer in part (b).
It is therefore possible that (R1)(A0) may be awarded, but (R0)(A1) can never be awarded.
Note: Simple examples of determining the validity of an argument without the use of a truth table may be tested.