Question
When Andy plays tennis, \(65\% \) of his first serves go into the correct area of the court.
If the first serve goes into the correct area, his chance of winning the point is \(90\% \).
If his first serve does not go into the correct area, Andy is allowed a second serve and, of these, \(80\% \) go into the correct area.
If the second serve goes into the correct area, his chance of winning the point is \(60\% \).
If neither serve goes into the correct area, Andy loses the point.
Complete the tree diagram below.
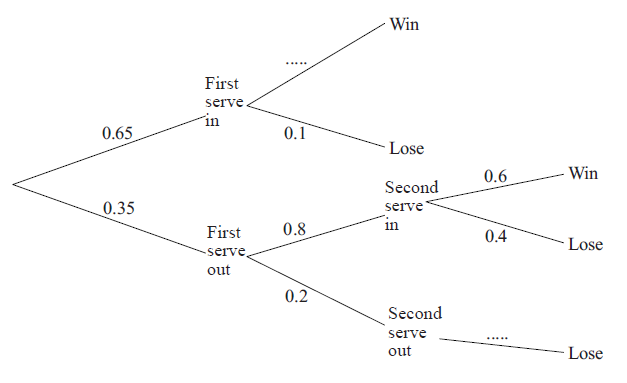[2]
Find the probability that Andy loses the point.[4]
Answer/Explanation
Markscheme
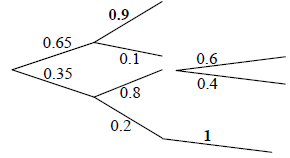(A1)(A1) (C2)[2 marks]
\(0.65 \times 0.1\) (\( = 0.065\)) (A1)
\(0.35 \times 0.8 \times 0.4\) (\( = 0.112\)) (A1)
\(0.35 \times 0.2 \times 1\) the 1 can be implied (\( = 0.07\)) (A1)(ft)
0.247 (A1)(ft) (C4)
Note: No (ft) for any probabilities greater than 1.[4 marks]
Question
The probability that it will snow tomorrow is 0.3.
If it snows tomorrow the probability that Chuck will be late for school is 0.8.
If it does not snow tomorrow the probability that Chuck will be late for school is 0.1.
Complete the tree diagram below.
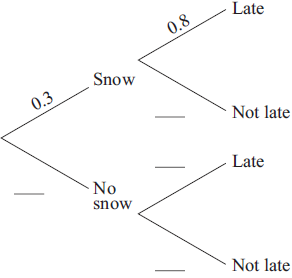[3]
Find the probability that it does not snow tomorrow and Chuck is late for school.[1]
Find the probability that Chuck is late for school.[2]
Answer/Explanation
Markscheme
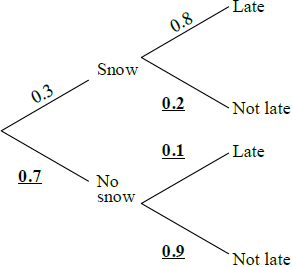(A1)(A1)(A1) (C3)
Note: Award (A1) for each correct pair.[3 marks]
\(0.7 \times 0.1\)
\( = 0.07(\frac{7}{{100}},{\text{ }}7\% )\) (A1)(ft) (C1)[1 mark]
\(0.3 \times 0.8 + 0.07\) (M1)
\( = 0.31(\frac{{31}}{{100}},{\text{ }}31\% )\) (A1)(ft)
Note: In (b) and (c) follow through from sensible answers only i.e. not a probability greater than one. (C2)[2 marks]
Question
Maria travels to school either by walking or by bicycle. The probability she cycles to school is 0.75.
If she walks, the probability that she is late for school is 0.1.
If she cycles, the probability that she is late for school is 0.05.
Complete the tree diagram below, showing the appropriate probabilities.
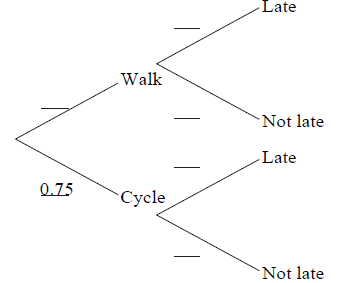[3]
Find the probability that Maria is late for school.[3]
Answer/Explanation
Markscheme
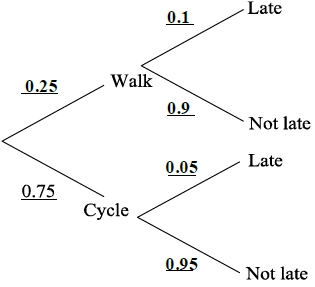(A1)(A1)(A1) (C3)
Note: Award (A1) for 0.25, (A1) for 0.1 and 0.9, (A1) for 0.05 and 0.95[3 marks]
\({\text{P}}({\text{late}}) = 0.25 \times 0.1 + 0.75 \times 0.05\) (A1)(ft)(M1)
Note: Award (A1)(ft) for two correct products from their diagram and award (M1) for addition of their two products.
\( = 0.0625\left( {\frac{1}{{16}},{\text{ }}6.25\% } \right)\) (A1)(ft) (C3)[3 marks]
Question
A survey was carried out in a group of 200 people. They were asked whether they smoke or not. The collected information was organized in the following table.
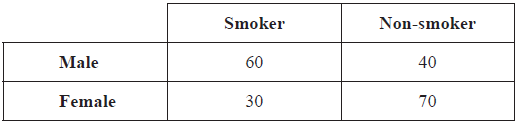
One person from this group is chosen at random.
Write down the probability that this person is a smoker.[2]
Write down the probability that this person is male given that they are a smoker.[2]
Find the probability that this person is a smoker or is male.[2]
Answer/Explanation
Markscheme
\(\frac{{90}}{{200}}(0.45,{\text{ }}45{\text{ }}\% )\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{{60}}{{90}}(0.\bar 6,{\text{ }}0.667,{\text{ }}66.\bar 6{\text{ }}\% ,{\text{ }}66.6 \ldots {\text{ }}\% ,{\text{ }}66.7{\text{ }}\% )\) (A1)(A1)(ft) (C2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator, follow through from their numerator in part (a). Last mark is lost if answer is not a probability.[2 marks]
\(\frac{{90}}{{200}} + \frac{{100}}{{200}} – \frac{{60}}{{200}}\) (M1)
Note: Award (M1) for correct substitution in the combined events formula. Follow through from their answer to part (a).
\( = \frac{{130}}{{200}}(0.65,{\text{ }}65{\text{ }}\% )\) (A1)(ft)
OR
\(\frac{{60}}{{200}} + \frac{{40}}{{200}} + \frac{{30}}{{200}}\) (M1)
Note: Award (M1) for adding the correct fractions.
\( = \frac{{130}}{{200}}(0.65,{\text{ }}65{\text{ }}\% )\) (A1)
OR
\(1 – \frac{{70}}{{200}}\) (M1)
Note: Award (M1) for subtraction of correct fraction from 1.
\( = \frac{{130}}{{200}}(0.65,{\text{ }}65{\text{ }}\% )\) (A1) (C2)[2 marks]
Question
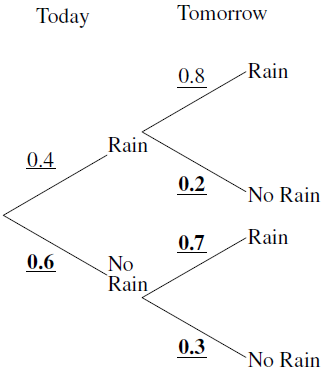
The probability that it rains today is \(0.4\) . If it rains today, the probability that it will rain tomorrow is \(0.8\) . If it does not rain today, the probability that it will rain tomorrow is \(0.7\) .
Complete the tree diagram below.
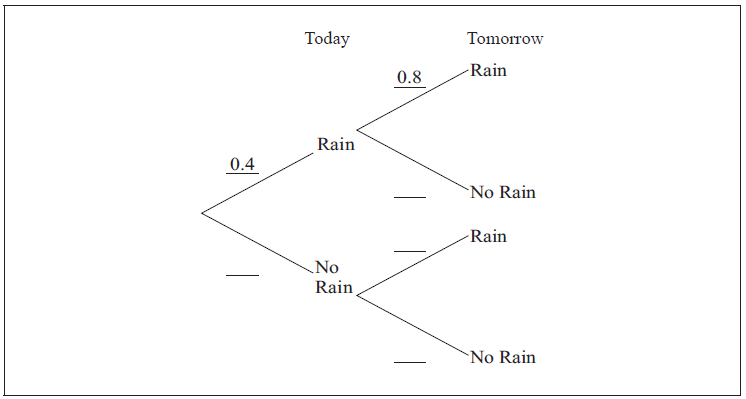[3]
Calculate the probability of rain tomorrow.[3]
Answer/Explanation
Markscheme
(A1)(A1)(A1) (C3)
Note: Award (A1) for each correct pair.[3 marks]
\(0.4 \times 0.8 + 0.6 \times 0.7\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for two consistent products from tree diagram, (M1) for addition of their products. Follow through from their tree diagram provided all probabilities are between 0 and 1.
\( = 0.74\) (A1)(ft) (C3)[3 marks]
Question
A survey was carried out at an international airport. A number of travellers were interviewed and asked for their flight destinations. The results are shown in the table below.
One traveller is to be chosen at random from all those interviewed.
Find the probability that this traveller was going to Africa.[2]
One female traveller is to be chosen at random from all those interviewed.
Find the probability that this female traveller was going to Asia.[2]
One traveller is to be chosen at random from those not going to America.
Find the probability that the chosen traveller is female.[2]
Answer/Explanation
Markscheme
\(\frac{{108}}{{250}}{\text{ }}\left( {\frac{{54}}{{125}}{\text{, }}0.432{\text{, }}43.2\% } \right)\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{{25}}{{106}}{\text{ }}\left( {0.236{\text{, }}23.6\% } \right)\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{{71}}{{170}}{\text{ }}\left( {0.418{\text{, }}41.8\% } \right)\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
Question
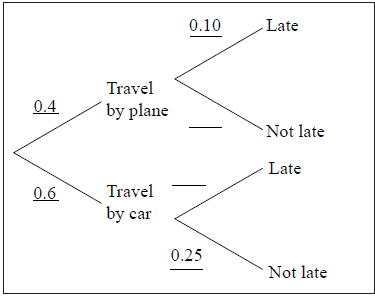
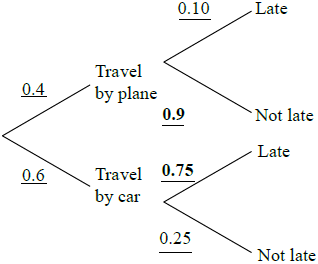
Merryn plans to travel to a concert tomorrow. Due to bad weather, there is a 60 % chance that all flights will be cancelled tomorrow. If the flights are cancelled Merryn will travel by car.
If she travels by plane the probability that she will be late for the concert is 10 %.
If she travels by car, the probability that she will not be late for the concert is 25 %.
Complete the tree diagram below.
[1]
Find the probability that Merryn will not be late for the concert.[3]
Merryn was not late for the concert the next day.
Given that, find the probability that she travelled to the concert by car.[2]
Answer/Explanation
Markscheme
(A1) (C1)
Note: Award (A1) for 0.9 and 0.75.[1 mark]
0.4 × 0.9 + 0.6 × 0.25 (M1)(M1)
Note: Award (M1) for their two relevant products, (M1) for adding their two products.
\(0.51\left( {\frac{{51}}{{100}},{\text{ }}51\% } \right)\) (A1)(ft) (C3)
Note: Follow through from their answers to part (a).[3 marks]
\(\frac{{0.6 \times 0.25}}{{0.51}}\) (M1)
Note: Award (M1) for correctly substituted conditional probability formula.
\(0.294\left( {\frac{5}{{17}}{\text{, }}0.294117…} \right)\) (A1)(ft) (C2)
Note: Follow through from their tree diagram and their part (b).[2 marks]
Question
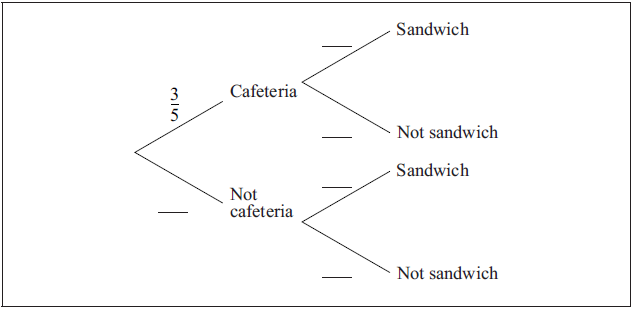
The probability that Tanay eats lunch in the school cafeteria is \(\frac{3}{5}\).
If he eats lunch in the school cafeteria, the probability that he has a sandwich is \(\frac{3}{{10}}\).
If he does not eat lunch in the school cafeteria the probability that he has a sandwich is \(\frac{9}{{10}}\).
Complete the tree diagram below.
[3]
Find the probability that Tanay has a sandwich for his lunch.[3]
Answer/Explanation
Markscheme
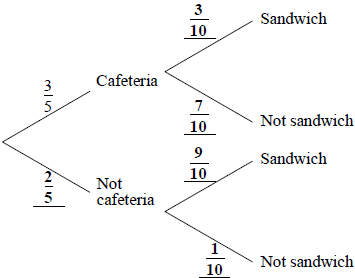(A1)(A1)(A1) (C3)
Note: Award (A1) for each correct pair of branches.
\(\frac{3}{5} \times \frac{3}{{10}} + \frac{2}{5} \times \frac{9}{{10}}\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for their two correct products, (M1) for addition of their products. Follow through from their tree diagram.
\( = \frac{{27}}{{50}}(0.54,54\% )\) (A1)(ft) (C3)
Question
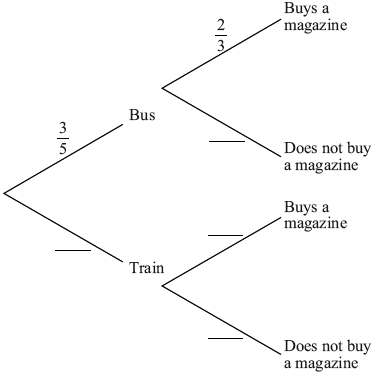
Ramzi travels to work each day, either by bus or by train. The probability that he travels by bus is \(\frac{3}{5}\). If he travels by bus, the probability that he buys a magazine is \(\frac{2}{3}\). If he travels by train, the probability that he buys a magazine is \(\frac{3}{4}\).
Complete the tree diagram.
[3]
Find the probability that Ramzi buys a magazine when he travels to work.[3]
Answer/Explanation
Markscheme
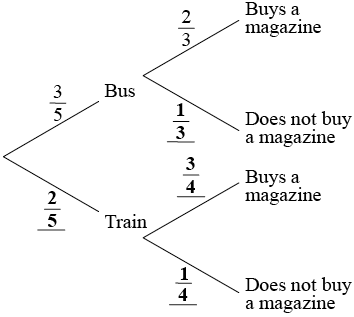(A1)(A1)(A1) (C3)
Note: Award (A1) for each correct pair of branches.[3 marks]
\(\frac{3}{5} \times \frac{2}{3} + \frac{2}{5} \times \frac{3}{4}\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for two consistent products from tree diagram, (M1) for addition of their products.
Follow through from their tree diagram provided all probabilities are between \(0\) and \(1\).
\(\frac{7}{{10}}{\text{ }}\left( {{\text{0.7, 70% , }}\frac{{42}}{{60}}} \right)\) (A1)(ft) (C3)[3 marks]
Question
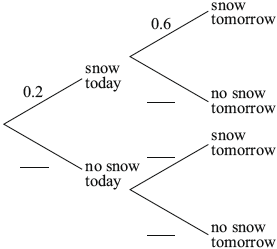
The probability that it snows today is 0.2. If it does snow today, the probability that it will snow tomorrow is 0.6. If it does not snow today, the probability that it will not snow tomorrow is 0.9.
Using the information given, complete the following tree diagram.
[3]
Calculate the probability that it will snow tomorrow.[3]
Answer/Explanation
Markscheme
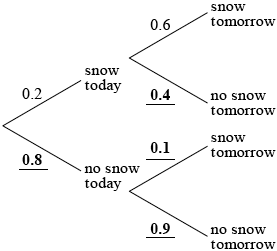(A1)(A1)(A1) (C3)
Note: Award (A1) for each correct pair of probabilities.[3 marks]
\(0.2 \times 0.6 + 0.8 \times 0.1\) (A1)(ft)(M1)
Note: Award (A1)(ft) for two correct products of probabilities taken from their diagram, (M1) for the addition of their products.
\( = 0.2{\text{ }}\left( {\frac{1}{5},{\text{ 20% }}} \right)\) (A1)(ft) (C3)
Note: Accept any equivalent correct fraction.
Follow through from their tree diagram.[3 marks]
Question
Aleph has an unbiased cubical (six faced) die on which are written the numbers
1 , 2 , 3 , 4 , 5 and 6.
Beth has an unbiased tetrahedral (four faced) die on which are written the numbers
2 , 3 , 5 and 7.
Complete the Venn diagram with the numbers written on Aleph’s die (\(A\)) and Beth’s die (\(B\)).
[2]
Find \(n(B \cap A’)\).[2]
Aleph and Beth are each going to roll their die once only. Shin says the probability that each die will show the same number is \(\frac{1}{8}\).
Determine whether Shin is correct. Give a reason.[2]
Answer/Explanation
Markscheme
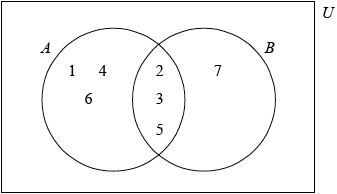(A1)(A1) (C2)
Note: Award (A1) for 2, 3, 5 in intersection, (A1) for 1, 4, 6, 7 correctly placed.
\(1\) (M1)(A1)(ft) (C2)
Notes: Award (M1)(A0) for listing the elements of their set \(B \cap A’\);shading the correct region on diagram; or an answer of \(1/7\) with a correct Venn diagram. Follow through from part (a).
Correct, from \((2,{\text{ }}2){\text{ }}(3,{\text{ }}3)\) and \((5,{\text{ }}5)\) on sample space
OR
Correct, from a labelled tree diagram
OR
Correct, from a sample space diagram
OR
Correct, from \(3 \times \frac{1}{4} \times \frac{1}{6}\;\;\;\)(or equivalent) (A1)(ft)(R1) (C2)
Notes: Do not award (A1)(ft)(R0). Award (R1) for a consistent reason with their part (a). Follow through from part (a).
Question
Peter either walks or cycles to work. The probability that he walks is 0.25. If Peter walks to work, the probability that he is late is 0.1. If he cycles to work, the probability that he is late is 0.05. The tree diagram for this information is shown.
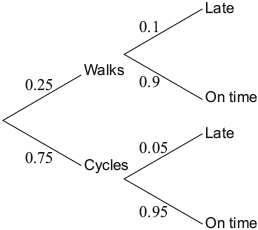
On a day chosen at random, Peter walked to work.
Write down the probability that he was on time.[1]
For a different day, also chosen at random,
find the probability that Peter cycled to work and was late.[2]
For a different day, also chosen at random,
find the probability that, given Peter was late, he cycled to work.[3]
Answer/Explanation
Markscheme
\(0.9\) (A1) (C1)
\(0.75 \times 0.05\) (M1)
\( = 0.0375\;\;\;\left( {\frac{3}{{80}},{\text{ 3,75% }}} \right)\) (A1) (C2)
\(\frac{{0.75 \times 0.05}}{{0.75 \times 0.05 + 0.25 \times 0.1}}\) (M1)(M1)
Note: Award (M1) for their correct numerator, (M1) for their correct denominator, ie, \(\left( {\frac{{{\text{their (b)}}}}{{{\text{their (b)}} + 0.25 \times 0.1}}} \right)\).
Do not award (M1) for their \(0.0375\) or \(0.0625\) if not a correct part of a fraction.
\( = 0.6\;\;\;\left( {\frac{3}{5},{\text{ }}60\% } \right)\) (A1)(ft) (C3)
Note: Follow through from part (b).
Question
On a work day, the probability that Mr Van Winkel wakes up early is \(\frac{4}{5}\).
If he wakes up early, the probability that he is on time for work is \(p\).
If he wakes up late, the probability that he is on time for work is \(\frac{1}{4}\).
The probability that Mr Van Winkel arrives on time for work is \(\frac{3}{5}\).
Complete the tree diagram below.
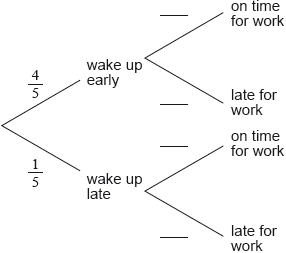[2]
Find the value of \(p\).[4]
Answer/Explanation
Markscheme
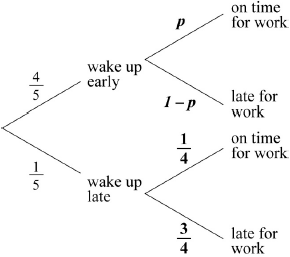(A1)(A1) (C2)
Note: Award (A1) for each correct pair of probabilities.[2 marks]
\(\frac{4}{5}p + \frac{1}{5} \times \frac{1}{4} = \frac{3}{5}\) (A1)(ft)(M1)(M1)
Note: Award (A1)(ft) for two correct products from part (a), (M1) for adding their products, (M1) for equating the sum of any two probabilities to \(\frac{3}{5}\).
\((p = ){\text{ }}\frac{{11}}{{16}}{\text{ }}(0.688,{\text{ }}0.6875)\) (A1)(ft) (C4)
Note: Award the final (A1)(ft) only if \(0 \leqslant p \leqslant 1\). Follow through from part (a).[4 marks]
Question
Dune Canyon High School organizes its school year into three trimesters: fall/autumn (\(F\)), winter (\(W\)) and spring (\(S\)). The school offers a variety of sporting activities during and outside the school year.
The activities offered by the school are summarized in the following Venn diagram.
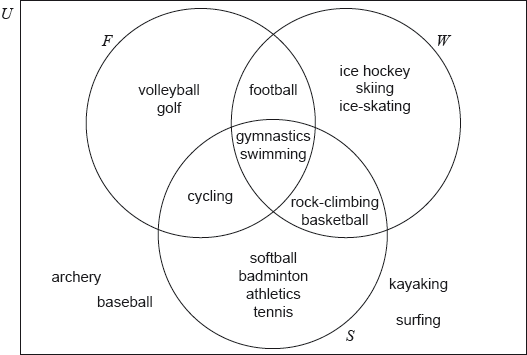
Write down the number of sporting activities offered by the school during its school year.[1]
Determine whether rock-climbing is offered by the school in the fall/autumn trimester.[1]
Write down the elements of the set \(F \cap W’\);[1]
Write down \(n(W \cap S)\).[1]
Write down, in terms of \(F\), \(W\) and \(S\), an expression for the set which contains only archery, baseball, kayaking and surfing.[2]
Answer/Explanation
Markscheme
15 (A1) (C1)[1 mark]
no (A1) (C1)
Note: Accept “it is only offered in Winter and Spring”.[1 mark]
volleyball, golf, cycling (A1) (C1)
Note: Responses must list all three sports for the (A1) to be awarded.[1 mark]
4 (A1) (C1)[1 mark]
\((F \cup W \cup S)’\)\(\,\,\,\)OR\(\,\,\,\)\(F’ \cap W’ \cap S’\) (or equivalent) (A2) (C2)[2 marks]
Question
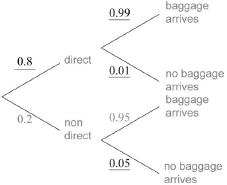
Sara regularly flies from Geneva to London. She takes either a direct flight or a non-directflight that goes via Amsterdam.
If she takes a direct flight, the probability that her baggage does not arrive in London is 0.01.
If she takes a non-direct flight the probability that her baggage arrives in London is 0.95.
The probability that she takes a non-direct flight is 0.2.
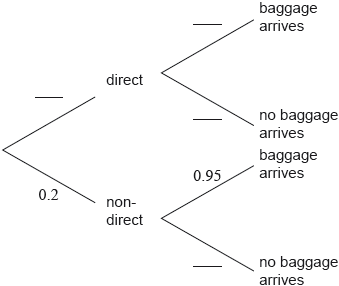
Complete the tree diagram.[3]
Find the probability that Sara’s baggage arrives in London.[3]
Answer/Explanation
Markscheme
(A1)(A1)(A1) (C3)
Note: Award (A1) for each correct pair of probabilities.[3 marks]
\(0.8 \times 0.99 + 0.2 \times 0.95\) (A1)(ft)(M1)
Note: Award (A1)(ft) for two correct products of probabilities taken from their diagram, (M1) for the addition of their products.
\( = 0.982{\text{ }}\left( {98.2\% ,{\text{ }}\frac{{491}}{{500}}} \right)\) (A1)(ft) (C3)
Note: Follow through from part (a).[3 marks]
Question
All the children in a summer camp play at least one sport, from a choice of football (\(F\)) or basketball (\(B\)). 15 children play both sports.
The number of children who play only football is double the number of children who play only basketball.
Let \(x\) be the number of children who play only football.
There are 120 children in the summer camp.
Write down an expression, in terms of \(x\), for the number of children who play only basketball.[1]
Complete the Venn diagram using the above information.
[2]
Find the number of children who play only football.[2]
Write down the value of \(n(F)\).[1]
Answer/Explanation
Markscheme
\(\frac{1}{2}x\) (A1) (C1)[1 mark]
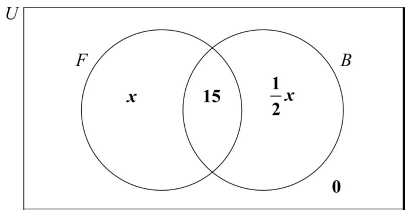(A1)(A1)(ft) (C2)
Notes: Award (A1) for 15 placed in the correct position, award (A1)(ft) for \(x\) and their \(\frac{1}{2}x\) placed in the correct positions of diagram. Do not penalize the absence of 0 inside the rectangle and award at most (A1)(A0) if any value other than 0 is seen outside the circles. Award at most (A1)(A0) if 35 and 70 are seen instead of \(x\) and their \(\frac{1}{2}x\).[2 marks]
\(x + \frac{1}{2}x + 15 = 120\) or equivalent (M1)
Note: Award (M1) for adding the values in their Venn and equating to 120 (or equivalent).
\((x = ){\text{ }}70\) (A1)(ft) (C2)
Note: Follow through from their Venn diagram, but only if the answer is a positive integer and \(x\) is seen in their Venn diagram.[2 marks]
85 (A1)(ft) (C1)
Note: Follow through from their Venn diagram and their answer to part (c), but only if the answer is a positive integer and less than 120.[1 mark]
Question
The Home Shine factory produces light bulbs, 7% of which are found to be defective.
Francesco buys two light bulbs produced by Home Shine.
The Bright Light factory also produces light bulbs. The probability that a light bulb produced by Bright Light is not defective is \(a\).
Deborah buys three light bulbs produced by Bright Light.
Write down the probability that a light bulb produced by Home Shine is not defective.[1]
Find the probability that both light bulbs are not defective.[2]
Find the probability that at least one of Francesco’s light bulbs is defective.[2]
Write down an expression, in terms of \(a\), for the probability that at least one of Deborah’s three light bulbs is defective.[1]
Answer/Explanation
Markscheme
0.93 (93%) (A1) (C1)[1 mark]
\(0.93 \times 0.93\) (M1)
Note: Award (M1) for squaring their answer to part (a).
0.865 (0.8649; 86.5%) (A1)(ft) (C2)
Notes: Follow through from part (a).
Accept \(0.86{\text{ }}\left( {{\text{unless it follows }}\frac{{93}}{{100}} \times \frac{{92}}{{99}}} \right)\).[2 marks]
\(1 – 0.8649\) (M1)
Note: Follow through from their answer to part (b)(i).
OR
\(0.07 \times 0.07 + 2 \times (0.07 \times 0.93)\) (M1)
Note: Follow through from part (a).
0.135 (0.1351; 13.5%) (A1)(ft) (C2)[2 marks]
\(1 – {a^3}\) (A1) (C1)
Note: Accept \(3{a^2}(1 – a) + 3a{(1 – a)^2} + {(1 – a)^3}\) or equivalent.[1 mark]
Question
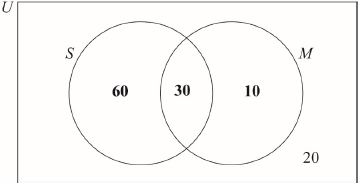
Rosewood College has 120 students. The students can join the sports club (\(S\)) and the music club (\(M\)).
For a student chosen at random from these 120, the probability that they joined both clubs is \(\frac{1}{4}\) and the probability that they joined the music club is\(\frac{1}{3}\).
There are 20 students that did not join either club.
Complete the Venn diagram for these students.
[2]
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.[2]
Determine whether the events \(S\) and \(M\) are independent.[2]
Answer/Explanation
Markscheme
(A1)(A1) (C2)
Note: Award (A1) for 30 in correct area, (A1) for 60 and 10 in the correct areas.[2 marks]
\(\frac{{30}}{{90}}{\text{ }}\left( {\frac{1}{3},{\text{ }}0.333333 \ldots ,{\text{ }}33.3333 \ldots \% } \right)\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for correct numerator of 30, (A1)(ft) for correct denominator of 90. Follow through from their Venn diagram.[2 marks]
\({\text{P}}(S) \times {\text{P}}(M) = \frac{3}{4} \times \frac{1}{3} = \frac{1}{4}\) (R1)
Note: Award (R1) for multiplying their by \(\frac{1}{3}\).
therefore the events are independent \(\left( {{\text{as P}}(S \cap M) = \frac{1}{4}} \right)\) (A1)(ft) (C2)
Note: Award (R1)(A1)(ft) for an answer which is consistent with their Venn diagram.
Do not award (R0)(A1)(ft).
Do not award final (A1) if \({\text{P}}(S) \times {\text{P}}(M)\) is not calculated. Follow through from part (a).[2 marks]
Question
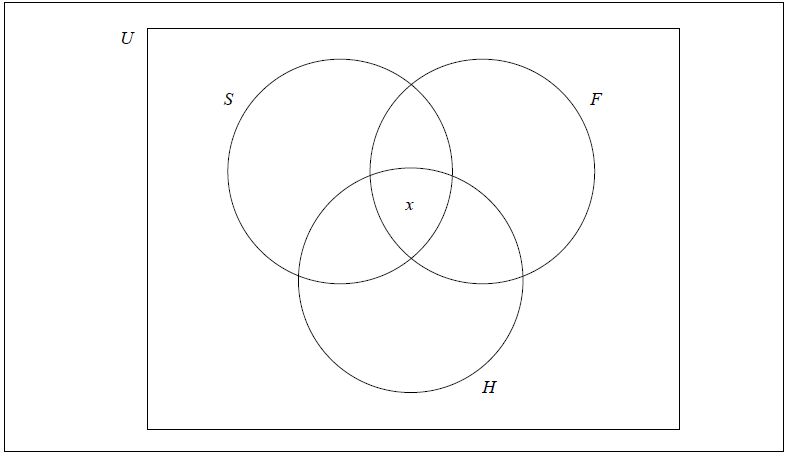
A group of 60 sports enthusiasts visited the PyeongChang 2018 Winter Olympic games to watch a variety of sporting events.
The most popular sports were snowboarding (S), figure skating (F) and ice hockey (H).
For this group of 60 people:
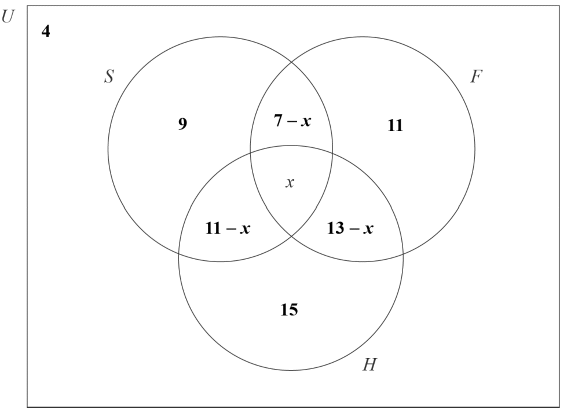
4 did not watch any of the most popular sports,
x watched all three of the most popular sports,
9 watched snowboarding only,
11 watched figure skating only,
15 watched ice hockey only,
7 watched snowboarding and figure skating,
13 watched figure skating and ice hockey,
11 watched snowboarding and ice hockey.
Complete the Venn diagram using the given information.
[3]
Find the value of x.[2]
Write down the value of \(n\left( {\left( {F \cup H} \right) \cap S’} \right)\).[1]
Answer/Explanation
Markscheme
(A1)(A1)(A1) (C3)
Note: Award (A1) for 4 in correct place.
Award (A1) for 9, 11, 15 in correct place.
Award (A1) for 7 − x, 13 − x, 11 − x in correct place.
Accept 2, 8 and 6 in place of 7 − x, 13 − x, 11 − x.[3 marks]
\(4 + 9 + 11 + 15 + x + \left( {7 – x} \right) + \left( {11 – x} \right) + \left( {13 – x} \right) = 60\) (M1)
Note: Award (M1) for equating the sum of at least seven of the entries in their Venn diagram to 60.
\(\left( {x = } \right)\,\,5\) (A1)(ft) (C2)
Note: Follow through from part (a), but only if answer is positive.[2 marks]
34 (A1)(ft) (C1)
Note: Follow through from their Venn diagram.[1 mark]