Download IITian Academy App for accessing Online Mock Tests and More..
Question
P (4, 1) and Q (0, –5) are points on the coordinate plane.
Determine the
(i) coordinates of M, the midpoint of P and Q.
(ii) gradient of the line drawn through P and Q.
(iii) gradient of the line drawn through M, perpendicular to PQ.[4]
The perpendicular line drawn through M meets the y-axis at R (0, k).
Find k.[2]
Answer/Explanation
Markscheme
(i) (2, – 2) parentheses not required. (A1)
(ii) gradient of PQ \( = \left( {\frac{{ – 5 – 1}}{{0 – 4}}} \right) = \frac{6}{4} = \frac{3}{2}(1.5)\) (M1)(A1)
(M1) for gradient formula with correct substitution
Award (A1) for \(y = \frac{3}{2}x – 5\) with no other working
(iii) gradient of perpendicular is \( – \frac{2}{3}\) (A1)(ft) (C4)[4 marks]
\(\left( {\frac{{k + 2}}{{0 – 2}}} \right) = – \frac{2}{3}\), \(k = – \frac{2}{3}\) or \(y = – \frac{2}{3}x + c\), \(c = – \frac{2}{3}\therefore k = – \frac{2}{3}\) (M1)(A1)(ft)
Allow (\(0, – \frac{2}{3}\))
(M1) is for equating gradients or substituting gradient into \(y = mx + c\) (C2)[2 marks]
Question
A store sells bread and milk. On Tuesday, 8 loaves of bread and 5 litres of milk were sold for $21.40. On Thursday, 6 loaves of bread and 9 litres of milk were sold for $23.40.
If \(b =\) the price of a loaf of bread and \(m =\) the price of one litre of milk, Tuesday’s sales can be written as \(8b + 5m = 21.40\).
Using simplest terms, write an equation in b and m for Thursday’s sales.[2]
Find b and m.[2]
Draw a sketch, in the space provided, to show how the prices can be found graphically.
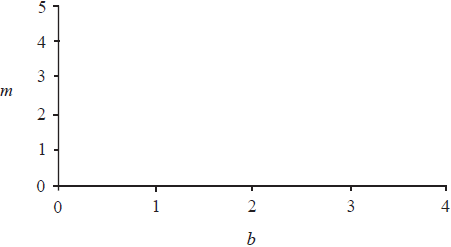[2]
Answer/Explanation
Markscheme
Thursday’s sales, \(6b + 9m = 23.40\) (A1)
\(2b + 3m = 7.80\) (A1) (C2)[2 marks]
\(m = 1.40\) (accept 1.4) (A1)(ft)
\(b = 1.80\) (accept 1.8) (A1)(ft)
Award (A1)(d) for a reasonable attempt to solve by hand and answer incorrect. (C2)[2 marks]
(A1)(A1)(ft)
(A1) each for two reasonable straight lines. The intersection point must be approximately correct to earn both marks, otherwise penalise at least one line.
Note: The follow through mark is for candidate’s line from (a). (C2)[2 marks]
Question
The mid-point, M, of the line joining A(s , 8) to B(−2, t) has coordinates M(2, 3).
Calculate the values of s and t.[2]
Find the equation of the straight line perpendicular to AB, passing through the point M.[4]
Answer/Explanation
Markscheme
\(s = 6\) (A1)
\(t = – 2\) (A1) (C2)[2 marks]
\({\text{gradient of AB}} = \frac{{ – 2 – 8}}{{ – 2 – 6}} = \frac{{ – 10}}{{ – 8}} = \frac{5}{4}\) (A1)(ft)
(A1) for gradient of AM or BM \( = \frac{5}{4}\)
\({\text{Perpendicular gradient}} = – \frac{4}{5}\) (A1)(ft)
Equation of perpendicular bisector is
\(y = – \frac{4}{5}x + c\)
\(3 = – \frac{4}{5}(2) + c\) (M1)
\(c = 4.6\)
\(y = -0.8x + 4.6\)
or \(5y = -4x + 23\) (A1)(ft) (C4)[4 marks]
Question
Write down the gradient of the line \(y = 3x + 4\).[1]
Find the gradient of the line which is perpendicular to the line \(y = 3x + 4\).[1]
Find the equation of the line which is perpendicular to \(y = 3x + 4\) and which passes through the point \((6{\text{, }}7)\).[2]
Find the coordinates of the point of intersection of these two lines.[2]
Answer/Explanation
Markscheme
\(3\) (A1) (C1)[1 mark]
\( – 1/3\) (ft) from (a) (A1)(ft) (C1)[1 mark]
Substituting \((6{\text{, }}7)\) in \(y ={\text{their }}mx + c\) or equivalent to find \(c\). (M1)
\(y = \frac{{ – 1}}{3}x + 9\) or equivalent (A1)(ft) (C2)[2 marks]
\((1.5{\text{, }}8.5)\) (A1)(A1)(ft) (C2)
Note: Award (A1) for \(1.5\), (A1) for \(8.5\). (ft) from (c), brackets not required.[2 marks]
Question
A straight line, \({L_1}\) , has equation \(x + 4y + 34 = 0\) .
Find the gradient of \({L_1}\) .[2]
The equation of line \({L_2}\) is \(y = mx\) . \({L_2}\) is perpendicular to \({L_1}\) .
Find the value of \(m\).[2]
The equation of line \({L_2}\) is \(y = mx\) . \({L_2}\) is perpendicular to \({L_1}\) .
Find the coordinates of the point of intersection of the lines \({L_1}\) and \({L_2}\) .[2]
Answer/Explanation
Markscheme
\(4y = – x – 34\) or similar rearrangement (M1)
\({\text{Gradient}} = – \frac{1}{4}\) (A1) (C2)
\(m = 4\) (A1)(ft)(A1)(ft) (C2)
Note: (A1) Change of sign
(A1) Use of reciprocal[2 marks]
Reasonable attempt to solve equations simultaneously (M1)
\(( – 2{\text{, }} – 8)\) (A1)(ft) (C2)
Note: Accept \(x = – 2\) \(y = – 8\). Award (A0) if brackets not included.[2 marks]
Question
A and B are points on a straight line as shown on the graph below.
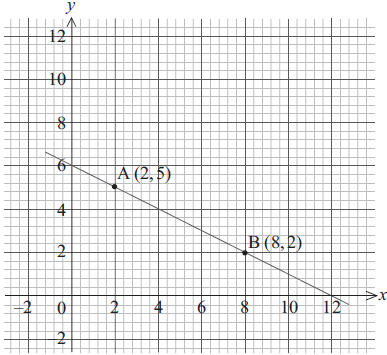
Write down the y-intercept of the line AB.[1]
Calculate the gradient of the line AB.[2]
The acute angle between the line AB and the x-axis is θ.
Show θ on the diagram.[1]
The acute angle between the line AB and the x-axis is θ.
Calculate the size of θ.[2]
Answer/Explanation
Markscheme
6
OR
(0, 6) (A1) (C1)[1 mark]
\(\frac{{(2 – 5)}}{{(8 – 2)}}\) (M1)
Note: Award (M1) for substitution in gradient formula.
\( = – \frac{1}{2}\) (A1) (C2)[2 marks]
Angle clearly identified. (A1) (C1)[1 mark]
\(\tan \theta = \frac{1}{2}\) (or equivalent fraction) (M1)
\(\theta = 26.6^\circ\) (A1)(ft) (C2)
Note: (ft) from (b).
Accept alternative correct trigonometrical methods.[2 marks]
Question
The straight line, L, has equation \(2y – 27x – 9 = 0\).
Find the gradient of L.[2]
Sarah wishes to draw the tangent to \(f (x) = x^4\) parallel to L.
Write down \(f ′(x)\).[1]
Find the x coordinate of the point at which the tangent must be drawn.[2]
Write down the value of \(f (x)\) at this point.[1]
Answer/Explanation
Markscheme
y = 13.5x + 4.5 (M1)
Note: Award (M1) for 13.5x seen.
gradient = 13.5 (A1) (C2)[2 marks]
4x3 (A1) (C1)[1 mark]
4x3 = 13.5 (M1)
Note: Award (M1) for equating their answers to (a) and (b).
x = 1.5 (A1)(ft)[2 marks]
\(\frac{{81}}{{16}}\) (5.0625, 5.06) (A1)(ft) (C3)
Note: Award (A1)(ft) for substitution of their (c)(i) into x4 with working seen.[1 mark]
Question
The diagram below shows the line PQ, whose equation is x + 2y = 12. The line intercepts the axes at P and Q respectively.
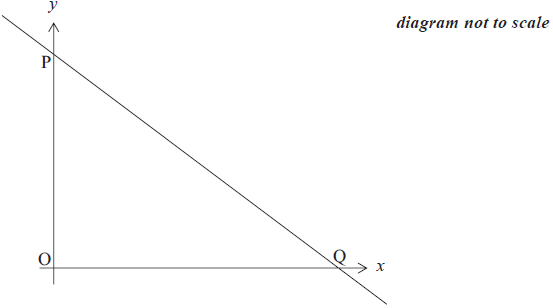
Find the coordinates of P and of Q.[3]
A second line with equation x − y = 3 intersects the line PQ at the point A. Find the coordinates of A.[3]
Answer/Explanation
Markscheme
\(0 + 2y = 12\) or \(x + 2(0) = 12\) (M1)
P(0, 6) (accept \(x = 0\), \(y = 6\)) (A1)
Q(12, 0) (accept \(x = 12\), \(y = 0\)) (A1) (C3)
Notes: Award (M1) for setting either value to zero.
Missing coordinate brackets receive (A0) the first time this occurs.
Award (A0)(A1)(ft) for P(0, 12) and Q(6, 0).[3 marks]
\(x + 2(x – 3) = 12\) (M1)
(6, 3) (accept \(x = 6\), \(y = 3\)) (A1)(A1) (C3)
Note: (A1) for each correct coordinate.
Missing coordinate brackets receive (A0)(A1) if this is the first time it occurs.[3 marks]
Question
The coordinates of the vertices of a triangle ABC are A (4, 3), B (7, –3) and C (0.5, p).
Calculate the gradient of the line AB.[2]
Given that the line AC is perpendicular to the line AB
write down the gradient of the line AC.[1]
Given that the line AC is perpendicular to the line AB
find the value of p.[3]
Answer/Explanation
Markscheme
\(m({\rm{AB}}) = \frac{{ – 3 – 3}}{{7 – 4}} = – 2\) (M1)(A1) (C2)
Note: Award (M1) for attempt to substitute into correct gradient formula.[2 marks]
\(m({\rm{AC}}) = \frac{1}{2}\) (A1)(ft)[1 mark]
\(\frac{{p – 3}}{{0.5 – 4}} = \frac{1}{2}\) (or equivalent method) (M1)(A1)(ft)
Note: Award (M1) for equating gradient to \(\frac{1}{2}\). (A1) for correct substitution.
\(p = 1.25\) (A1)(ft) (C4)[3 marks]
Question
Consider \(f:x \mapsto {x^2} – 4\).
Find \(f ′(x)\).[1]
Let L be the line with equation y = 3x + 2.
Write down the gradient of a line parallel to L.[1]
Let L be the line with equation y = 3x + 2.
Let P be a point on the curve of f. At P, the tangent to the curve is parallel to L. Find the coordinates of P.[4]
Answer/Explanation
Markscheme
\(2x\) (A1) (C1)[1 mark]
3 (A1) (C1)[1 mark]
\(2x = 3\) (M1)
Note: (M1) for equating their (a) to their (b).
\(x =1.5\) (A1)(ft)
\(y = (1.5)^2 – 4\) (M1)
Note: (M1) for substituting their x in f (x).
(1.5, −1.75) (accept x = 1.5, y = −1.75) (A1)(ft) (C4)
Note: Missing coordinate brackets receive (A0) if this is the first time it occurs.[4 marks]
Question
A line joins the points A(2, 1) and B(4, 5).
Find the gradient of the line AB.[2]
Let M be the midpoint of the line segment AB.
Write down the coordinates of M.[1]
Let M be the midpoint of the line segment AB.
Find the equation of the line perpendicular to AB and passing through M.[3]
Answer/Explanation
Markscheme
\({\text{Gradient}} = \frac{{(5 – 1)}}{{(4 – 2)}}\) (M1)
Note: Award (M1) for correct substitution in the gradient formula.
\(= 2\) (A1) (C2)[2 marks]
Midpoint = (3, 3) (accept x = 3, y = 3 ) (A1) (C1)[1 mark]
\({\text{Gradient of perpendicular}} = -\frac{{1}}{{2}}\) (A1)(ft)
\(y = – \frac{{1}}{{2}} x + c\) (M1)
\(3 = – \frac{{1}}{{2}} \times 3 + c\)
\(c = 4.5\)
\(y = -0.5x + 4.5\) (A1)(ft)
OR
\(y – 3 = -0.5(x – 3)\) (A1)(A1)(ft)
Note: Award (A1) for –0.5, (A1) for both threes.
OR
\(2y + x = 9\) (A1)(A1)(ft) (C3)
Note: Award (A1) for 2, (A1) for 9.[3 marks]
Question
The straight line, L1, has equation \(y = – \frac{1}{2}x – 2\).
Write down the y intercept of L1.[1]
Write down the gradient of L1.[1]
The line L2 is perpendicular to L1 and passes through the point (3, 7).
Write down the gradient of the line L2.[1]
The line L2 is perpendicular to L1 and passes through the point (3, 7).
Find the equation of L2. Give your answer in the form ax + by + d = 0 where \(a,{\text{ }}b,{\text{ }}d \in \mathbb{Z}\).[3]
Answer/Explanation
Markscheme
–2 (A1) (C1)
Note: Accept (0, –2).[1 mark]
\( – \frac{1}{2}\) (A1) (C1)[1 mark]
2 (A1)(ft) (C1)
Note: Follow through from their answer to part (b).1 mark]
y = 2x + c (can be implied)
7 = 2 × 3 + c (M1)
c = 1 (A1)(ft)
y = 2x + 1
Notes: Award (M1) for substitution of (3, 7), (A1)(ft) for c.
Follow through from their answer to part (c).
OR
y – 7 = 2(x – 3) (M1)(M1)
Note: Award (M1) for substitution of their answer to part (c), (M1) for substitution of (3, 7).
2x – y + 1 = 0 or –2x + y – 1 = 0 (A1)(ft) (C3)
Note: Award (A1)(ft) for their equation in the stated form.[3 marks]
Question
The following diagrams show six lines with equations of the form y =mx +c.
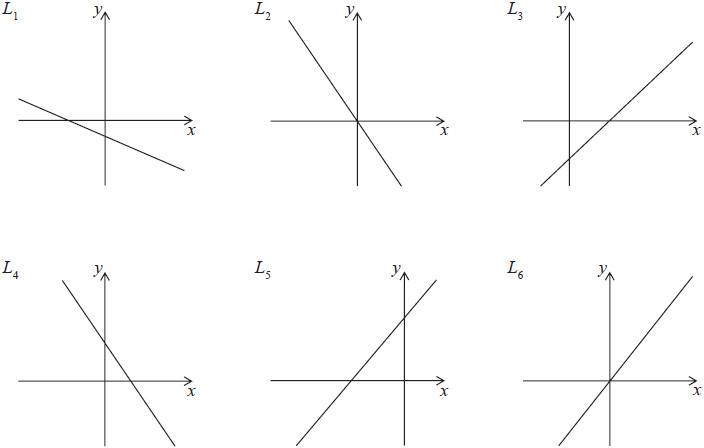
In the table below there are four possible conditions for the pair of values m and c. Match each of the given conditions with one of the lines drawn above.
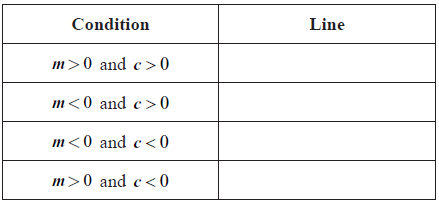
Answer/Explanation
Answer/Explanation
Markscheme
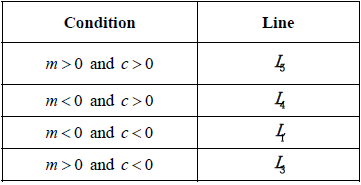(A6) (C6)
Notes: Award (A6) for all correct, (A5) for 3 correct, (A3) for 2 correct, (A1) for 1 correct.
Deduct (A1) for any repetition.[6 marks]
Question
The diagram shows the straight lines \({L_1}\) and \({L_2}\) . The equation of \({L_2}\) is \(y = x\) .
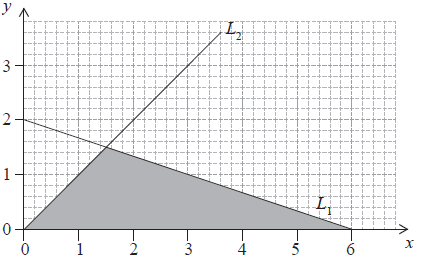
Find
(i) the gradient of \({L_1}\) ;
(ii) the equation of \({L_1}\) .[3]
Find the area of the shaded triangle.[2]
Answer/Explanation
Markscheme
(i) \(\frac{{0 – 2}}{{6 – 0}}\) (M1)
\( = – \frac{1}{3}{\text{ }}\left( { – \frac{2}{6}{\text{, }} – 0.333} \right)\) (A1) (C2)
(ii) \(y = – \frac{1}{3}x + 2\) (A1)(ft) (C1)
Notes: Follow through from their gradient in part (a)(i). Accept equivalent forms for the equation of a line.[3 marks]
\({\text{area}} = \frac{{6 \times 1.5}}{2}\) (A1)(M1)
Note: Award (A1) for \(1.5\) seen, (M1) for use of triangle formula with \(6\) seen.
\( = 4.5\) (A1) (C3)[2 marks]
Question
The equation of the line \({R_1}\) is \(2x + y – 8 = 0\) . The line \({R_2}\) is perpendicular to \({R_1}\) .
Calculate the gradient of \({R_2}\) .[2]
The point of intersection of \({R_1}\) and \({R_2}\) is \((4{\text{, }}k)\) .
Find
(i) the value of \(k\) ;
(ii) the equation of \({R_2}\) .[4]
Answer/Explanation
Markscheme
\(y = – 2x + 8\) (M1)
Note: Award (M1) for rearrangement of equation or for \( – 2\) seen.
\(m({\text{perp}}) = \frac{1}{2}\) (A1) (C2)[2 marks]
(i) \(2(4) + k – 8 = 0\) (M1)
Note: Award (M1) for evidence of substituting \(x = 4\) into \({R_1}\) .
\(k = 0\) (A1) (C2)
(ii) \(y = \frac{1}{2}x + c\) (can be implied) (M1)
Note: Award (M1) for substitution of \(\frac{1}{2}\) into equation of the line.
\(0 = \frac{1}{2}(4) + c\)
\(y = \frac{1}{2}x – 2\) (A1)(ft) (C2)
Notes: Follow through from parts (a) and (b)(i). Accept equivalent forms for the equation of a line.
OR
\(y – {y_1} = \frac{1}{2}(x – {x_1})\) (M1)
Note: Award (M1) for substitution of \(\frac{1}{2}\) into equation of the line.
\(y = \frac{1}{2}(x – 4)\) (A1)(ft) (C2)
Notes: Follow through from parts (a) and (b)(i). Accept equivalent forms for the equation of a line.[4 marks]
Question
The straight line \(L\) passes through the points \({\text{A}}( – 1{\text{, 4}})\) and \({\text{B}}(5{\text{, }}8)\) .
Calculate the gradient of \(L\) .[2]
Find the equation of \(L\) .[2]
The line \(L\) also passes through the point \({\text{P}}(8{\text{, }}y)\) . Find the value of \(y\) .[2]
Answer/Explanation
Markscheme
\(\frac{{8 – 4}}{{5 – ( – 1)}}\) (M1)
Note: Award (M1) for correct substitution into the gradient formula.
\(\frac{2}{3}{\text{ }}\left( {\frac{4}{6}{\text{, }}0.667} \right)\) (A1) (C2)[2 marks]
\(y = \frac{2}{3}x + c\) (A1)(ft)
Note: Award (A1)(ft) for their gradient substituted in their equation.
\(y = \frac{2}{3}x + \frac{{14}}{3}\) (A1)(ft) (C2)
Notes: Award (A1)(ft) for their correct equation. Accept any equivalent form. Accept decimal equivalents for coefficients to 3 sf.
OR
\(y – {y_1} = \frac{2}{3}(x – {x_1})\) (A1)(ft)
Note: Award (A1)(ft) for their gradient substituted in the equation.
\(y – 4 = \frac{2}{3}(x + 1)\) OR \(y – 8 = \frac{2}{3}(x – 5)\) (A1)(ft) (C2)
Note: Award (A1)(ft) for correct equation.[2 marks]
\(y = \frac{2}{3} \times 8 + \frac{{14}}{3}\) OR \(y – 4 = \frac{2}{3}(8 + 1)\) OR \(y – 8 = \frac{2}{3}(8 – 5)\) (M1)
Note: Award (M1) for substitution of \(x = 8\) into their equation.
\(y = 10\) (\(10.0\)) (A1)(ft) (C2)
Note: Follow through from their answer to part (b).[2 marks]
Question
The diagram shows points A(2, 8), B(14, 4) and C(4, 2). M is the midpoint of AC.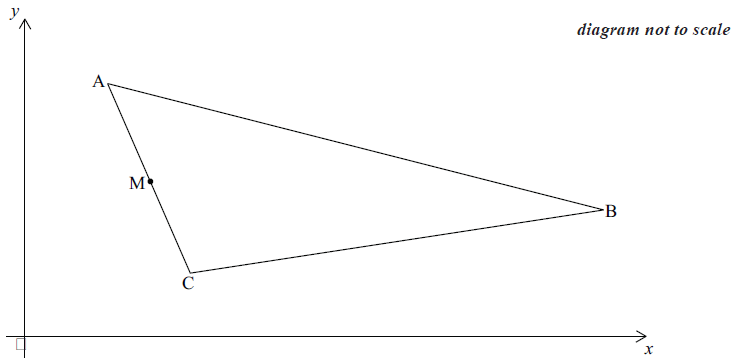
Write down the coordinates of M.[2]
Calculate the gradient of the line AB.[2]
Find the equation of the line parallel to AB that passes through M.[2]
Answer/Explanation
Markscheme
\(\left( {\frac{{2 + 4}}{2},\frac{{8 + 2}}{2}} \right)\) (M1)
Note: Award (M1) for a correct substitution into the midpoint formula.
\( = (3, 5)\) (A1) (C2)
Note: Brackets must be present for final (A1) to be awarded.
Note: Accept \(x = 3\), \(y = 5\) .[2 marks]
\(\frac{{8 – 4}}{{2 – 14}}\) (M1)
Note: Award (M1) for correctly substituted formula.
\( = – \frac{1}{3}\) \(\left( {\frac{{ – 4}}{{12}}, – 0.333} \right)\) \(( – 0.333333 \ldots )\) (A1) (C2)[2 marks]
\((y – 5) = – \frac{1}{3}(x – 3)\) (M1)(A1)(ft)
OR
\(5 = – \frac{1}{3}(3) + c\) (M1)
\(y = – \frac{1}{3}x + 6\) (A1)(ft) (C2)
Notes: Award (M1) for substitution of their gradient into equation of line with their values from (a) correctly substituted.
Accept correct equivalent forms of the equation of the line. Follow through from their parts (a) and (b).[2 marks]
Question
Line L is given by the equation 3y + 2x = 9 and point P has coordinates (6 , –5).
Explain why point P is not on the line L.[1]
Find the gradient of line L.[2]
(i) Write down the gradient of a line perpendicular to line L.
(ii) Find the equation of the line perpendicular to L and passing through point P.[3]
Answer/Explanation
Markscheme
3 × (–5) + 2 × 6 ≠ 9 (A1) (C1)
Note: Also accept 3 × (–5) + 2x = 9 gives x =12 ≠ 6 or 3y + 2 × (6) = 9 gives y = –1 ≠ –5.[1 mark]
3y = –2x + 9 (M1)
Note: Award (M1) for 3y = –2x + 9 or \(y = \frac{{ – 2}}{3}x + 3\) or \(y = \frac{{( – 2x + 9)}}{3}\).
\({\text{gradient}} = – \frac{2}{3}( – 0.667)( – 0.666666…)\) (A1) (C2)[2 marks]
(i) gradient of perpendicular line \( = \frac{3}{2}(1.5)\) (A1)(ft)
Note: Follow through from their answer to part (b).
(ii) \(y = \frac{3}{2}x + c\)
\( – 5 = \frac{3}{2} \times 6 + c\) (M1)
Note: Award (M1) for substitution of their perpendicular gradient and the point (6, –5) into the equation of their line.
\(y = \frac{3}{2}x – 14\) (A1)(ft)
Note: Follow through from their perpendicular gradient. Accept equivalent forms.
OR
\(y + 5 = \frac{3}{2}(x – 6)\) (M1)(A1)(ft) (C3)
Notes: Award (M1) for substitution of their perpendicular gradient and the point (6, –5) into the equation of their line. Follow through from their perpendicular gradient.[3 marks]
Question
The equation of a curve is given as \(y = 2x^{2} – 5x + 4\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
The equation of the line L is \(6x + 2y = -1\).
Find the x-coordinate of the point on the curve \(y = 2x^2 – 5x + 4\) where the tangent is parallel to L.[4]
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 4x – 5\) (A1)(A1) (C2)
Notes: Award (A1) for each correct term. Award (A1)(A0) if any other terms are given.[2 marks]
\(y = – 3x – \frac{1}{2}\) (M1)
Note: Award (M1) for rearrangement of equation
gradient of line is –3 (A1)
\(4x – 5 = -3\) (M1)
Notes: Award (M1) for equating their gradient to their derivative from part (a). If \(4x – 5 = -3\) is seen with no working award (M1)(A1)(M1).
\(x = \frac{1}{2}\) (A1)(ft) (C4)
Note: Follow through from their part (a). If answer is given as (0.5, 2) with no working award the final (A1) only.[4 marks]
Question
The straight line, L1, has equation y = −2x + 5.
Write down the gradient of L1 .[1]
Line L2, is perpendicular to line L1, and passes through the point (4, 5) .
(i) Write down the gradient of L2 .
(ii) Find the equation of L2 .[3]
Line L2, is perpendicular to line L1, and passes through the point (4, 5) .
Write down the coordinates of the point of intersection of L1 and L2 [2]
Answer/Explanation
Markscheme
–2 (A1) (C1)
Note: Do not accept \(\frac{{ – 2}}{1}\)[1 mark]
(i) \(\frac{1}{2}(0.5)\) (A1)(ft)
Note: Follow through from their part (a).
(ii) \(5 = \frac{1}{2}(4) + c\) (M1)
Note: Award (M1) for their gradient substituted correctly.
\(y = \frac{1}{2}x + 3\) (A1)(ft)
Note: Follow through from their part (b)(i).
OR
\(y – 5 = \frac{1}{2}(x – 4)\) (M1)(A1)(ft) (C3)
Notes: Award (M1) for their gradient substituted correctly, (A1)(ft) for 5 and 4 seen in the correct places. Follow through from their part (b)(i).[3 marks]
(0.8, 3.4) or \(\left( {\frac{4}{5},\frac{{17}}{5}} \right)\) (A1)(ft)(A1)(ft) (C2)
Notes: Accept x = 0.8 and y = 3.4. Award (A1)(ft) for an attempt to solve the equations analytically, (attempt to eliminate either x or y), or graphically with a sketch (two reasonably accurate straight line graphs (from their answer to part (b)) and an indication of scale). Follow through from their L2 if it intersects L1, OR follow through from their equation, or expression in x, from their part (b)(ii). Award at most (A1)(ft)(A0)(ft) if brackets missing. Award (A0)(ft)(A1)(ft) for an answer of (0, 5) following an equation (or expression in x) of the form y = mx + 5 (m ≠ –2) found in part (b).[2 marks]
Question
The straight line, L1, has equation \(2y − 3x =11\). The point A has coordinates (6, 0).
Give a reason why L1 does not pass through A.[1]
Find the gradient of L1.[2]
L2 is a line perpendicular to L1. The equation of L2 is \(y = mx + c\).
Write down the value of m.[1]
L2 does pass through A.
Find the value of c.[2]
Answer/Explanation
Markscheme
\(2 \times 0 – 3 \times 6 \ne 11\) (R1)
Note: Stating \(2 \times 0 – 3 \times 6 = – 18\) without a conclusion is not sufficient.
OR
Clear sketch of L1 and A.
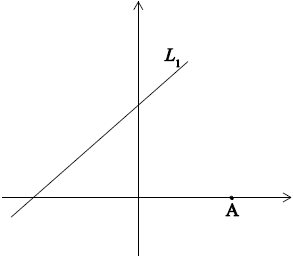(R1)
OR
Point A is (6, 0) and \(2y – 3x = 11\) has x-intercept at \(- \frac{11}{3}\) or the line has only one x-intercept which occurs when x is negative. (R1) (C1)
\(2y = 3x + 11\) or \(y – \frac{3}{2}x = \frac{{11}}{2}\) (M1)
Note: Award (M1) for a correct first step in making y the subject of the equation.
\(({\text{gradient equals}}) = \frac{3}{2}(1.5)\) (A1) (C2)
Note: Do not accept 1.5x.
\((m = ) – \frac{2}{3}\) (A1)(ft) (C1)
Notes: Follow through from their part (b).
\(0 = – \frac{2}{3}(6) + c\) (M1)
Note: Award (M1) for correct substitution of their gradient and (6, 0) into any form of the equation.
(c =) 4 (A1)(ft) (C2)
Note: Follow through from part (c).
Question
The equation of a line L1 is \(2x + 5y = −4\).
Write down the gradient of the line L1.[1]
A second line L2 is perpendicular to L1.
Write down the gradient of L2.[1]
The point (5, 3) is on L2.
Determine the equation of L2.[2]
Lines L1 and L2 intersect at point P.
Using your graphic display calculator or otherwise, find the coordinates of P.[2]
Answer/Explanation
Markscheme
\(\frac{-2}{{5}}\) (A1) (C1)
\(\frac{5}{{2}}\) (A1)(ft) (C1)
Note: Follow through from their answer to part (a).
\(3 = \frac{5}{2} \times 5 + c\) (M1)
Notes: Award (M1) for correct substitution of their gradient into equation of line. Follow through from their answer to part (b).
\(y = \frac{5}{2}x – \frac{19}{2}\) (A1)(ft)
OR
\(y – 3 = \frac{5}{2}(x – 5)\) (M1)(A1)(ft) (C2)
Notes: Award (M1) for correct substitution of their gradient into equation of line. Follow through from their answer to part (b).
(3, −2) (A1)(ft)(A1)(ft) (C2)
Notes: If parentheses not seen award at most (A0)(A1)(ft). Accept x = 3, y = −2. Follow through from their answer to part (c), even if no working is seen. Award (M1)(A1)(ft) for a sensible attempt to solve \(2x + 5y = −4\) and their \(y = \frac{5}{2}x – \frac{19}{2}\) or equivalent, simultaneously.
Question
The diagram shows the points M(a, 18) and B(24, 10) . The straight line BM intersects the y-axis at A(0, 26). M is the midpoint of the line segment AB.
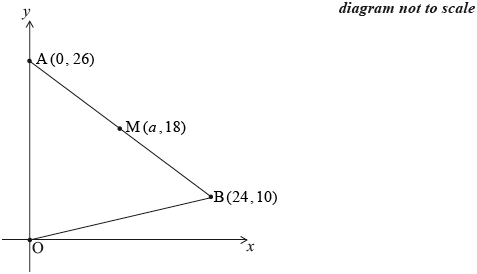
Write down the value of \(a\).[1]
Find the gradient of the line AB.[2]
Decide whether triangle OAM is a right-angled triangle. Justify your answer.[3]
Answer/Explanation
Markscheme
12 (A1) (C1)
Note: Award (A1) for \(\left( {12,18} \right)\).[1 mark]
\(\frac{{26 – 10}}{{0 – 24}}\) (M1)
Note: Accept \(\frac{{26 – 18}}{{0 – 12}}\) or \(\frac{{18 – 10}}{{12 – 24}}\) (or equivalent).
\( = – \frac{2}{3}{\text{ }}\left( { – \frac{{16}}{{24}},{\text{ }} – 0.666666 \ldots } \right)\) (A1) (C2)
Note: If either of the alternative fractions is used, follow through from their answer to part (a).
The answer is now (A1)(ft).[2 marks]
gradient of \({\text{OM}} = \frac{3}{2}\) (A1)(ft)
Note: Follow through from their answer to part (b).
\( – \frac{2}{3} \times \frac{3}{2}\) (M1)
Note: Award (M1) for multiplying their gradients.
Since the product is \(-1\), OAM is a right-angled triangle (R1)(ft)
Notes: Award the final (R1) only if their conclusion is consistent with their answer for the product of the gradients.
The statement that OAM is a right-angled triangle without justification is awarded no marks.
OR
\({(26 – 18)^2} + {12^2}\) and \({12^2} + {18^2}\) (A1)(ft)
\(\left( {{{(26 – 18)}^2} + {{12}^2}} \right) + ({12^2} + {18^2}) = {26^2}\) (M1)
Note: This method can also be applied to triangle OMB.
Follow through from (a).
Hence a right angled triangle (R1)(ft)
Note: Award the final (R1) only if their conclusion is consistent with their (M1) mark.
OR
\(OA = OB = 26\) (cm) an isosceles triangle (A1)
Note: Award (A1) for \(OA = 26\) (cm) and \(OB = 26\) (cm).
Line drawn from vertex to midpoint of base is perpendicular to the base (M1)
Conclusion (R1) (C3)
Note: Award, at most (A1)(M0)(R0) for stating that OAB is an isosceles triangle without any calculations.[3 marks]
Question
Let \(f(x) = {x^4}\).
Write down \(f'(x)\).[1]
Point \({\text{P}}(2,6)\) lies on the graph of \(f\).
Find the gradient of the tangent to the graph of \(y = f(x)\) at \({\text{P}}\).[2]
Point \({\text{P}}(2,16)\) lies on the graph of \(f\).
Find the equation of the normal to the graph at \({\text{P}}\). Give your answer in the form \(ax + by + d = 0\), where \(a\), \(b\) and \(d\) are integers.[3]
Answer/Explanation
Markscheme
\(\left( {f'(x) = } \right)\) \(4{x^3}\) (A1) (C1)[1 mark]
\(4 \times {2^3}\) (M1)
Note: Award (M1) for substituting 2 into their derivative.
\( = 32\) (A1)(ft) (C2)
Note: Follow through from their part (a).[2 marks]
\(y – 16 = – \frac{1}{{32}}(x – 2)\) or \(y = – \frac{1}{{32}}x + \frac{{257}}{{16}}\) (M1)(M1)
Note: Award (M1) for their gradient of the normal seen, (M1) for point substituted into equation of a straight line in only \(x\) and \(y\) (with any constant ‘\(c\)’ eliminated).
\(x + 32y – 514 = 0\) or any integer multiple (A1)(ft) (C3)
Note: Follow through from their part (b).[3 marks]
Question
The diagram shows a wheelchair ramp, \({\text{A}}\), designed to descend from a height of \(80{\text{ cm}}\).
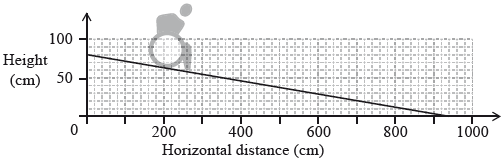
Use the diagram above to calculate the gradient of the ramp.[1]
The gradient for a safe descending wheelchair ramp is \( – \frac{1}{{12}}\).
Using your answer to part (a), comment on why wheelchair ramp \({\text{A}}\) is not safe.[1]
The equation of a second wheelchair ramp, B, is \(2x + 24y – 1920 = 0\).
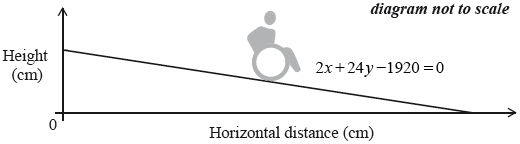
(i) Determine whether wheelchair ramp \({\text{B}}\) is safe or not. Justify your answer.
(ii) Find the horizontal distance of wheelchair ramp \({\text{B}}\).[4]
Answer/Explanation
Markscheme
\( – \frac{{80}}{{940}}{\text{ }}\left( {-0.0851, -0.085106 \ldots , -\frac{4}{{47}}} \right)\) (A1) (C1)[1 mark]
\(-0.0851{\text{ }} (-0.085106 \ldots ) < – \frac{1}{{12}}(-0.083333 \ldots )\) (A1)(ft) (C1)
Notes: Accept “less than” in place of inequality.
Award (A0) if incorrect inequality seen.
Follow through from part (a).[1 mark]
(i) ramp \({\text{B}}\) is safe (A1)
the gradient of ramp \({\text{B}}\) is \( – \frac{1}{{12}}\) (R1)
Notes: Award (R1) for “the gradient of ramp \({\text{B}}\) is \( – \frac{1}{{12}}\)” seen.
Do not award (A1)(R0).
(ii) \(2x = 1920\) (M1)
Note: Accept alternative methods.
\(960 {\text{ (cm)}}\) (A1) (C4)[4 marks]
Question
The number of apartments in a housing development has been increasing by a constant amount every year.
At the end of the first year the number of apartments was 150, and at the end of the sixth year the number of apartments was 600.
The number of apartments, \(y\), can be determined by the equation \(y = mt + n\), where \(t\) is the time, in years.
Find the value of \(m\).[2]
State what \(m\) represents in this context.[1]
Find the value of \(n\).[2]
State what \(n\) represents in this context.[1]
Answer/Explanation
Markscheme
\(\frac{{600 – 150}}{{6 – 1}}\) (M1)
OR
\(600 = 150 + (6 – 1)m\) (M1)
Note: Award (M1) for correct substitution into gradient formula or arithmetic sequence formula.
\( = 90\) (A1) (C2)
the annual rate of growth of the number of apartments (A1) (C1)
Note: Do not accept common difference.
\(150 = 90 \times (1) + n\) (M1)
Note: Award (M1) for correct substitution of their gradient and one of the given points into the equation of a straight line.
\(n = 60\) (A1)(ft) (C2)
Note: Follow through from part (a).
the initial number of apartments (A1) (C1)
Note: Do not accept “first number in the sequence”.
Question
The diagram shows the straight line \({L_1}\), which intersects the \(x\)-axis at \({\text{A}}(6,{\text{ }}0)\) and the \(y\)-axis at \({\text{B}}(0,{\text{ }}2)\) .
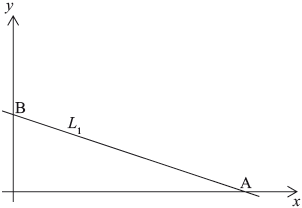
Write down the coordinates of M, the midpoint of line segment AB.[2]
Calculate the gradient of \({L_1}\).[2]
The line \({L_2}\) is parallel to \({L_1}\) and passes through the point \((3,{\text{ }}2)\).
Find the equation of \({L_2}\). Give your answer in the form \(y = mx + c\).[2]
Answer/Explanation
Markscheme
\((3,{\text{ }}1)\) (A1)(A1) (C2)
Note: Accept \(x = 3\), \(y = 1\). Award (A0)(A1) if parentheses are missing.
\(\frac{{2 – 0}}{{0 – 6}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = – \frac{1}{3}( – 0.333333 \ldots )\) (A1) (C2)
Note: Accept \( – \frac{2}{6}\).
\((y – 2) = – \frac{1}{3}(x – 3)\) (M1)
OR
\(2 = – \frac{1}{3}(3) + c\) (M1)
Note: Award (M1) for substitution of their gradient from part (b).
\(y = – \frac{1}{3}x + 3\) (A1)(ft) (C2)
Note: Follow through from part (b).
The answer must be an equation in the form \(y = mx + c\) for the (A1)(ft) to be awarded.
Question
The equation of the line \({L_1}\) is \(2x + y = 10\).
Write down
(i) the gradient of \({L_1}\);
(ii) the \(y\)-intercept of \({L_1}\).[2]
The line \({L_2}\) is parallel to \({L_1}\) and passes through the point \({\text{P}}(0,{\text{ }}3)\).
Write down the equation of \({L_2}\).[2]
The line \({L_2}\) is parallel to \({L_1}\) and passes through the point \({\text{P}}(0,{\text{ }}3)\).
Find the \(x\)-coordinate of the point where \({L_2}\) crosses the \(x\)-axis.[2]
Answer/Explanation
Markscheme
(i) \( – 2\) (A1) (C1)
(ii) \(10\) (A1) (C1)
\(2x + y – 3 = 0\) (A1)(ft)(A1) (C2)
Notes: Award (A1)(ft) for gradient, (A1) for correct \(y\)-intercept.
The answer must be an equation.
\( – 2x + 3 = 0\;\;\;\)or equivalent (M1)
\((x = ){\text{ }}1.5\) (A1)(ft) (C2)
Notes: Follow through from their equation in part (b). If answer given as coordinates \((1.5,{\text{ }}0)\) award at most (M1)(A0) if working seen or (A1)(A0) if no working seen.
Question
The equation of line \({L_1}\) is \(y = 2.5x + k\). Point \({\text{A}}\) \(\,(3,\, – 2)\) lies on \({L_1}\).
Find the value of \(k\).[2]
The line \({L_2}\) is perpendicular to \({L_1}\) and intersects \({L_1}\) at point \({\text{A}}\).
Write down the gradient of \({L_2}\).[1]
Find the equation of \({L_2}\). Give your answer in the form \(y = mx + c\) .[2]
Write your answer to part (c) in the form \(ax + by + d = 0\) where \(a\), \(b\) and \(d \in \mathbb{Z}\).[1]
Answer/Explanation
Markscheme
\( – 2 = 2.5\, \times 3 + k\) (M1)
Note: Award (M1) for correct substitution of \((3,\, – 2)\) into equation of \({L_1}\).
\((k = ) – 9.5\) (A1) (C2)
\( – 0.4\,\left( { – \frac{2}{5}} \right)\) (A1) (C1)
\(y – ( – 2) = – 0.4\,(x – 3)\) (M1)
OR
\( – 2 = – 0.4\,(3) + c\) (M1)
Note: Award (M1) for their gradient and given point substituted into equation of a straight line. Follow through from part (b).
\(y = – 0.4x – 0.8\) \(\left( {y = – \frac{2}{5}x – \frac{4}{5}} \right)\) (A1)(ft) (C2)
\(2x + 5y + 4 = 0\) (or any integer multiple) (A1)(ft) (C1)
Note: Follow through from part (c).
Question
The equation of the straight line \({L_1}\) is \(y = 2x – 3.\)
Write down the \(y\)-intercept of \({L_1}\) .[1]
Write down the gradient of \({L_1}\) .[1]
The line \({L_2}\) is parallel to \({L_1}\) and passes through the point \((0,\,\,3)\) .
Write down the equation of \({L_2}\) .[1]
The line \({L_3}\) is perpendicular to \({L_1}\) and passes through the point \(( – 2,\,\,6).\)
Write down the gradient of \({L_3}.\)[1]
Find the equation of \({L_3}\) . Give your answer in the form \(ax + by + d = 0\) , where \(a\) , \(b\) and \(d\) are integers.[2]
Answer/Explanation
Markscheme
\((0,\,\, – 3)\) (A1) (C1)
Note: Accept \( – 3\) or \(y = – 3.\)
\(2\) (A1) (C1)
\(y = 2x + 3\) (A1)(ft) (C1)
Note: Award (A1)(ft) for correct equation. Follow through from part (b)
Award (A0) for \({L_2} = 2x + 3\).
\( – \frac{1}{2}\) (A1)(ft) (C1)
Note: Follow through from part (b).
\(6 = – \frac{1}{2}( – 2) + c\) (M1)
\(c = 5\) (may be implied)
OR
\(y – 6 = – \frac{1}{2}(x + 2)\) (M1)
Note: Award (M1) for correct substitution of their gradient in part (d) and the point \(( – 2,\,\,6)\). Follow through from part (d).
\(x + 2y – 10 = 0\) (or any integer multiple) (A1)(ft) (C2)
Note: Follow through from (d). The answer must be in the form \(ax + by + d = 0\) for the (A1)(ft) to be awarded. Accept any integer multiple.
Question
The equation of line \({L_1}\) is \(y = – \frac{2}{3}x – 2\).
Point P lies on \({L_1}\) and has \(x\)-coordinate \( – 6\).
The line \({L_2}\) is perpendicular to \({L_1}\) and intersects \({L_1}\) when \(x = – 6\).
Write down the gradient of \({L_1}\).[1]
Find the \(y\)-coordinate of P.[2]
Determine the equation of \({L_2}\). Give your answer in the form \(ax + by + d = 0\), where \(a\), \(b\) and \(d\) are integers.[3]
Answer/Explanation
Markscheme
\( – \frac{2}{3}\) (A1) (C1)[1 mark]
\(y = – \frac{2}{3}( – 6) – 2\) (M1)
Note: Award (M1) for correctly substituting \( – 6\) into the formula for \({L_1}\).
\((y = ){\text{ }}2\) (A1) (C2)
Note: Award (A0)(A1) for \(( – 6,{\text{ }}2)\) with or without working.[2 marks]
gradient of \({L_2}\) is \(\frac{3}{2}\) (A1)(ft)
Note: Follow through from part (a).
\(2 = \frac{3}{2}( – 6) + c\)\(\,\,\,\)OR\(\,\,\,\)\(y – 2 = \frac{3}{2}\left( {x – ( – 6)} \right)\) (M1)
Note: Award (M1) for substituting their part (b), their gradient and \( – 6\) into equation of a straight line.
\(3x – 2y + 22 = 0\) (A1)(ft) (C3)
Note: Follow through from parts (a) and (b). Accept any integer multiple.
Award (A1)(M1)(A0) for \(y = \frac{3}{2}x + 11\).[3 marks]
Question
Line \(L\) intersects the \(x\)-axis at point A and the \(y\)-axis at point B, as shown on the diagram.
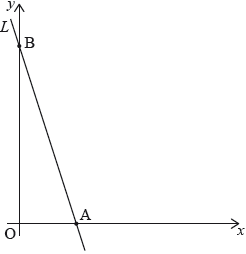
The length of line segment OB is three times the length of line segment OA, where O is the origin.
Point \({\text{(2, 6)}}\) lies on \(L\).
Find the gradient of \(L\).[2]
Find the equation of \(L\) in the form \(y = mx + c\).[2]
Find the \(x\)-coordinate of point A.[2]
Answer/Explanation
Markscheme
\( – 3\) (A1)(A1) (C2)
Notes: Award (A1) for 3 and (A1) for a negative value.
Award (A1)(A0) for either \(3x\) or \( – 3x\).[2 marks]
\(6 = – 3(2) + c\)\(\,\,\,\)OR\(\,\,\,\)\((y – 6) = – 3(x – 2)\) (M1)
Note: Award (M1) for substitution of their gradient from part (a) into a correct equation with the coordinates \((2,{\text{ }}6)\) correctly substituted.
\(y = – 3x + 12\) (A1)(ft) (C2)
Notes: Award (A1)(ft) for their correct equation. Follow through from part (a).
If no method seen, award (A1)(A0) for \(y = – 3x\).
Award (A1)(A0) for \( – 3x + 12\).[2 marks]
\(0 = – 3x + 12\) (M1)
Note: Award (M1) for substitution of \(y = 0\) in their equation from part (b).
\((x = ){\text{ }}4\) (A1)(ft) (C2)
Notes: Follow through from their equation from part (b). Do not follow through if no method seen. Do not award the final (A1) if the value of \(x\) is negative or zero.[2 marks]
Question
The coordinates of point A are \((6,{\text{ }} – 7)\) and the coordinates of point B are \(( – 6,{\text{ }}2)\). Point M is the midpoint of AB.
\({L_1}\) is the line through A and B.
The line \({L_2}\) is perpendicular to \({L_1}\) and passes through M.
Find the coordinates of M.[2]
Find the gradient of \({L_1}\).[2]
Write down the gradient of \({L_2}\).[1]
Write down, in the form \(y = mx + c\), the equation of \({L_2}\).[1]
Answer/Explanation
Markscheme
\((0,{\text{ }}2.5)\)\(\,\,\,\)OR\(\,\,\,\)\(\left( {0,{\text{ }} – \frac{5}{2}} \right)\) (A1)(A1) (C2)
Note: Award (A1) for 0 and (A1) for –2.5 written as a coordinate pair. Award at most (A1)(A0) if brackets are missing. Accept “\(x = 0\) and \(y = – 2.5\)”.[2 marks]
\(\frac{{2 – ( – 7)}}{{ – 6 – 6}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = – \frac{3}{4}{\text{ }}( – 0.75)\) (A1) (C2)[2 marks]
\(\frac{4}{3}{\text{ }}(1.33333 \ldots )\) (A1)(ft) (C1)
Note: Award (A0) for \(\frac{1}{{0.75}}\). Follow through from part (b).[1 mark]
\(y = \frac{4}{3}x – \frac{5}{2}{\text{ }}(y = 1.33 \ldots x – 2.5)\) (A1)(ft) (C1)
Note: Follow through from parts (c)(i) and (a). Award (A0) if final answer is not written in the form \(y = mx + c\).[1 mark]
Question
Consider the functions \(f\left( x \right) = {x^4} – 2\) and \(g\left( x \right) = {x^3} – 4{x^2} + 2x + 6\)
The functions intersect at points P and Q. Part of the graph of \(y = f\left( x \right)\) and part of the graph of \(y = g\left( x \right)\) are shown on the diagram.
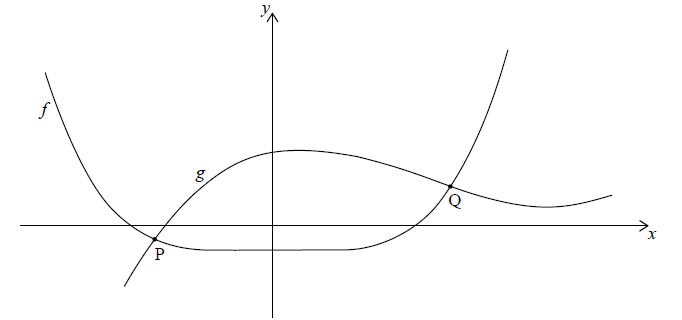
Find the range of f.[2]
Write down the x-coordinate of P and the x-coordinate of Q.[2]
Write down the values of x for which \(f\left( x \right) > g\left( x \right)\).[2]
Answer/Explanation
Markscheme
\(\left[ { – 2,\,\,\infty } \right[{\text{ or }}\left[ { – 2,\,\,\infty } \right)\) OR \(f\left( x \right) \geqslant – 2{\text{ or }}y \geqslant – 2\) OR \( – 2 \leqslant f\left( x \right) < \infty \) (A1)(A1) (C2)
Note: Award (A1) for −2 and (A1) for completely correct mathematical notation, including weak inequalities. Accept \(f \geqslant – 2\).[2 marks]
–1 and 1.52 (1.51839…) (A1)(A1) (C2)
Note: Award (A1) for −1 and (A1) for 1.52 (1.51839).[2 marks]
\(x < – 1,\,\,\,x > 1.52\) OR \(\left( { – \infty ,\,\, – 1} \right) \cup \left( {1.52,\,\,\infty } \right)\). (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for both critical values in inequality or range statements such as \(x < – 1,\,\,\left( { – \infty ,\,\, – 1} \right),\,\,x > 1.52\,{\text{ or }}\left( {1.52,\,\,\infty } \right)\).
Award the second (A1)(ft) for correct strict inequality statements used with their critical values. If an incorrect use of strict and weak inequalities has already been penalized in (a), condone weak inequalities for this second mark and award (A1)(ft).[2 marks]
Question
In this question, give all answers to two decimal places.
Karl invests 1000 US dollars (USD) in an account that pays a nominal annual interest of 3.5%, compounded quarterly. He leaves the money in the account for 5 years.
Calculate the amount of money he has in the account after 5 years.[3]
Write down the amount of interest he earned after 5 years.[1]
Karl decides to donate this interest to a charity in France. The charity receives 170 euros (EUR). The exchange rate is 1 USD = t EUR.
Calculate the value of t.[2]
Answer/Explanation
Markscheme
\(1000{\left( {1 + \frac{{3.5}}{{4 \times 100}}} \right)^{4 \times 5}}\) (M1)(A1)
Note: Award (M1) for substitution in compound interest formula, (A1) for correct substitution.
OR
N = 5
I = 3.5
PV = 1000
P/Y = 1
C/Y = 4
Note: Award (A1) for C/Y = 4 seen, (M1) for other correct entries.
OR
N = 5 × 4
I = 3.5
PV = 1000
P/Y = 1
C/Y = 4
Note: Award (A1) for C/Y = 4 seen, (M1) for other correct entries.
= 1190.34 (USD) (A1)
Note: Award (M1) for substitution in compound interest formula, (A1) for correct substitution.[3 marks]
190.34 (USD) (A1)(ft) (C4)
Note: Award (A1)(ft) for subtraction of 1000 from their part (a)(i). Follow through from (a)(i).[1 mark]
\(\frac{{170}}{{190.34}}\) (M1)
Note: Award (M1) for division of 170 by their part (a)(ii).
= 0.89 (A1)(ft) (C2)
Note: Follow through from their part (a)(ii).[2 marks]