Question
Consider the functions \(f(x) = \frac{{2x + 3}}{{x + 4}}\) and \(g(x) = x + 0.5\) .
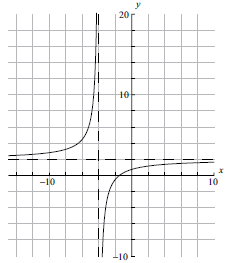
Sketch the graph of the function \(f(x)\), for \( – 10 \leqslant x \leqslant 10\) . Indicating clearly the axis intercepts and any asymptotes.[6]
Write down the equation of the vertical asymptote.[2]
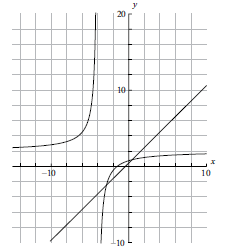
On the same diagram as part (a) sketch the graph of \(g(x) = x + 0.5\) .[2]
Using your graphical display calculator write down the coordinates of one of the points of intersection on the graphs of \(f\) and \(g\), giving your answer correct to five decimal places.[3]
Write down the gradient of the line \(g(x) = x + 0.5\) .[1]
The line \(L\) passes through the point with coordinates \(( – 2{\text{, }} – 3)\) and is perpendicular to the line \(g(x)\) . Find the equation of \(L\).[3]
Answer/Explanation
Markscheme
(A6)
Notes: (A1) for labels and some idea of scale.
(A1) for \(x\)-intercept seen, (A1) for \(y\)-intercept seen in roughly the correct places (coordinates not required).
(A1) for vertical asymptote seen, (A1) for horizontal asymptote seen in roughly the correct places (equations of the lines not required).
(A1) for correct general shape.[6 marks]
\(x = – 4\) (A1)(A1)(ft)
Note: (A1) for \(x =\), (A1)(ft) for \( – 4\).[2 marks]
(A1)(A1)
Note: (A1) for correct axis intercepts, (A1) for straight line[2 marks]
\(( – 2.85078{\text{, }} – 2.35078)\) OR \((0.35078{\text{, }}0.85078)\) (G1)(G1)(A1)(ft)
Notes: (A1) for \(x\)-coordinate, (A1) for \(y\)-coordinate, (A1)(ft) for correct accuracy. Brackets required. If brackets not used award (G1)(G0)(A1)(ft).
Accept \(x = – 2.85078\), \(y = – 2.35078\) or \(x = 0.35078\), \(y = 0.85078\).[3 marks]
\({\text{gradient}} = 1\) (A1)[1 mark]
\({\text{gradient of perpendicular}} = – 1\) (A1)(ft)
(can be implied in the next step)
\(y = mx + c\)
\( – 3 = – 1 \times – 2 + c\) (M1)
\(c = – 5\)
\(y = – x – 5\) (A1)(ft)(G2)
OR
\(y + 3 = – (x + 2)\) (M1)(A1)(ft)(G2)
Note: Award (G2) for correct answer with no working at all but (A1)(G1) if the gradient is mentioned as \( – 1\) then correct answer with no further working.[3 marks]
Question
Mal is shopping for a school trip. He buys \(50\) tins of beans and \(20\) packets of cereal. The total cost is \(260\) Australian dollars (\({\text{AUD}}\)).
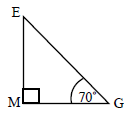
The triangular faces of a square based pyramid, \({\text{ABCDE}}\), are all inclined at \({70^ \circ }\) to the base. The edges of the base \({\text{ABCD}}\) are all \(10{\text{ cm}}\) and \({\text{M}}\) is the centre. \({\text{G}}\) is the mid-point of \({\text{CD}}\).
Write down an equation showing this information, taking \(b\) to be the cost of one tin of beans and \(c\) to be the cost of one packet of cereal in \({\text{AUD}}\).[1]
Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Write down another equation to represent this information.[1]
Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Find the cost of one tin of beans.[2]
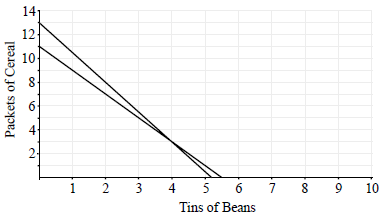
(i) Sketch the graphs of the two equations from parts (a) and (b).
(ii) Write down the coordinates of the point of intersection of the two graphs.[4]
Using the letters on the diagram draw a triangle showing the position of a \({70^ \circ }\) angle.[1]
Show that the height of the pyramid is \(13.7{\text{ cm}}\), to 3 significant figures.[2]
Calculate
(i) the length of \({\text{EG}}\);
(ii) the size of angle \({\text{DEC}}\).[4]
Find the total surface area of the pyramid.[2]
Find the volume of the pyramid.[2]
Answer/Explanation
Markscheme
\(50b + 20c = 260\) (A1)[1 mark]
\(12b + 6c = 66\) (A1)[1 mark]
Solve to get \(b = 4\) (M1)(A1)(ft)(G2)
Note: (M1) for attempting to solve the equations simultaneously.[2 marks]
(i)
(A1)(A1)(A1)
Notes: Award (A1) for labels and some idea of scale, (A1)(ft)(A1)(ft) for each line.
The axis can be reversed.
(ii) \((4,3)\) or \((3,4)\) (A1)(ft)
Note: Accept \(b = 4\), \(c = 3\)[4 marks]
(A1)[1 mark]
\(\tan 70 = \frac{h}{5}\) (M1)
\(h = 5\tan 70 = 13.74\) (A1)
\(h = 13.7{\text{ cm}}\) (AG)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
(i) \({\text{E}}{{\text{G}}^2} = {5^2} + {13.7^2}\) OR \({5^2} + {(5\tan 70)^2}\) (M1)
(UP) \({\text{EG}} = 14.6{\text{ cm}}\) (A1)(G2)
(ii) \({\text{DEC}} = 2 \times {\tan ^{ – 1}}\left( {\frac{5}{{14.6}}} \right)\) (M1)
\( = {37.8^ \circ }\) (A1)(ft)(G2)[4 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Area}} = 10 \times 10 + 4 \times 0.5 \times 10 \times 14.619\) (M1)
(UP) \( = 392{\text{ c}}{{\text{m}}^2}\) (A1)(ft)(G2)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Volume}} = \frac{1}{3} \times 10 \times 10 \times 13.7\) (M1)
(UP) \( = 457{\text{ c}}{{\text{m}}^3}\) (\(458{\text{ c}}{{\text{m}}^3}\)) (A1)(G2)[2 marks]
Question
Consider the function \(f:x \mapsto \frac{{kx}}{{{2^x}}}\).
The cost per person, in euros, when \(x\) people are invited to a party can be determined by the function
\(C(x) = x + \frac{{100}}{x}\)
Given that \(f(1) = 2\), show that \(k = 4\).[2]
Write down the values of \(q\) and \(r\) for the following table.
[2]
As \(x\) increases from \( – 1\), the graph of \(y = f(x)\) reaches a maximum value and then decreases, behaving asymptotically.
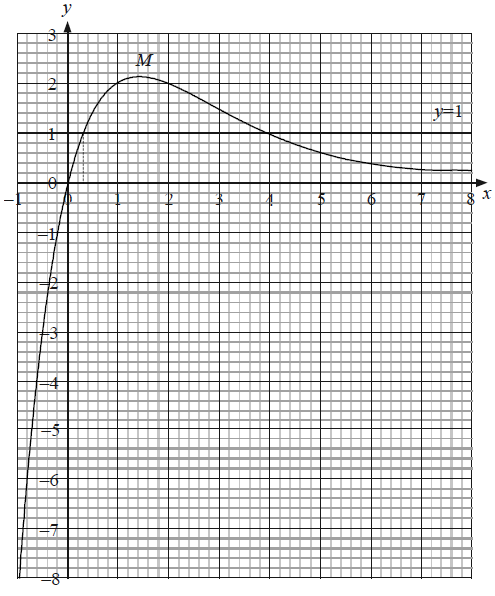
Draw the graph of \(y = f(x)\) for \( – 1 \leqslant x \leqslant 8\). Use a scale of \({\text{1 cm}}\) to represent 1 unit on both axes. The position of the maximum, \({\text{M}}\), the \(y\)-intercept and the asymptotic behaviour should be clearly shown.[4]
Using your graphic display calculator, find the coordinates of \({\text{M}}\), the maximum point on the graph of \(y = f(x)\).[2]
Write down the equation of the horizontal asymptote to the graph of \(y = f(x)\).[2]
(i) Draw and label the line \( y = 1\) on your graph.
(ii) The equation \(f(x) = 1\) has two solutions. One of the solutions is \(x = 4\). Use your graph to find the other solution.[4]
Find \(C'(x)\).[3]
Show that the cost per person is a minimum when \(10\) people are invited to the party.[2]
Calculate the minimum cost per person.[2]
Answer/Explanation
Markscheme
\(f(1) = \frac{k}{{{2^1}}}\) (M1)
Note: (M1) for substituting \(x = 1\) into the formula.
\(\frac{k}{2} = 2\) (M1)
Note: (M1) for equating to 2.
\(k = 4\) (AG)[2 marks]
\(q = 2\), \(r = 0.125\) (A1)(A1)[2 marks]
(A4)
Notes: (A1) for scales and labels.
(A1) for accurate smooth curve passing through \((0, 0)\) drawn at least in the given domain.
(A1) for asymptotic behaviour (curve must not go up or cross the \(x\)-axis).
(A1) for indicating the position of the maximum point.[4 marks]
\({\text{M}}\) (\(1.44\), \(2.12\)) (G1)(G1)
Note: Brackets required, if missing award (G1)(G0). Accept \(x = 1.44\) and \(y = 2.12\).[2 marks]
\(y = 0\) (A1)(A1)
Note: (A1) for ‘\(y = \)’ provided the right hand side is a constant. (A1) for 0.[2 marks]
(i) See graph (A1)(A1)
Note: (A1) for correct line, (A1) for label.
(ii) \(x = 0.3\) (ft) from candidate’s graph. (A2)(ft)
Notes: Accept \( \pm 0.1\) from their x. For \(0.310\) award (G1)(G0). For other answers taken from the GDC and not given correct to 3 significant figures award (G0)(AP)(G0) or (G1)(G0) if (AP) already applied.[4 marks]
\(C'(x) = 1 – \frac{{100}}{{{x^2}}}\) (A1)(A1)(A1)
Note: (A1) for 1, (A1) for \( – 100\) , (A1) for \({x^2}\) as denominator or \({{x^{ – 2}}}\) as numerator. Award a maximum of (A2) if an extra term is seen.[3 marks]
For studying signs of the derivative at either side of \(x = 10\) (M1)
For saying there is a change of sign of the derivative (M1)(AG)
OR
For putting \(x = 10\) into \(C’\) and getting zero (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
OR
For solving \(C'(x) = 0\) and getting \(10\) (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
Note: For a sketch with a clear indication of the minimum or for a table with values of \(x\) at either side of \(x = 10\) award (M1)(M0).[2 marks]
\(C(10) = 10 + \frac{{100}}{{10}}\) (M1)
\(C(10) = 20\) (A1)(G2)[2 marks]
Question
Throughout this question all the numerical answers must be given correct to the nearest whole number.
Park School started in January 2000 with \(100\) students. Every full year, there is an increase of \(6\% \) in the number of students.
Find the number of students attending Park School in
(i) January 2001;
(ii) January 2003.[4]
Park School started in January 2000 with \(100\) students. Every full year, there is an increase of \(6\% \) in the number of students.
Show that the number of students attending Park School in January 2007 is \(150\).[2]
Grove School had \(110\) students in January 2000. Every full year, the number of students is \(10\) more than in the previous year.
Find the number of students attending Grove School in January 2003.[2]
Grove School had \(110\) students in January 2000. Every full year, the number of students is \(10\) more than in the previous year.
Find the year in which the number of students attending Grove School will be first \(60\% \) more than in January 2000.[4]
Each January, one of these two schools, the one that has more students, is given extra money to spend on sports equipment.
(i) Decide which school gets the money in 2007. Justify your answer.
(ii) Find the first year in which Park School will be given this extra money.[5]
Answer/Explanation
Markscheme
(i) \(100 \times 1.06 = 106\) (M1)(A1)(G2)
Note: (M1) for multiplying by \(1.06\) or equivalent. (A1) for correct answer.
(ii) \(100 \times {1.06^3} = 119\) (M1)(A1)(G2)
Note: (M1) for multiplying by \({1.06^3}\) or equivalent or for list of values. (A1) for correct answer.[4 marks]
\(100 \times {1.06^7} = 150.36 \ldots = 150\) correct to the nearest whole (M1)(A1)(AG)
Note: (M1) for correct formula or for list of values. (A1) for correct substitution or for \(150\) in the correct position in the list. Unrounded answer must be seen for the (A1).[2 marks]
\(110 + 3 \times 10 = 140\) (M1)(A1)(G2)
Note: (M1) for adding \(30\) or for list of values. (A1) for correct answer.[2 marks]
In (d) and (e) follow through from (c) if consistent wrong use of correct AP formula.
\(110 + (n – 1) \times 10 > 176\) (A1)(M1)
\(n = 8\therefore {\text{year 2007}}\) (A1)(A1)(ft)(G2)
Note: (A1) for \(176\) or \(66\) seen. (M1) for showing list of values and comparing them to \(176\) or for equating formula to \(176\) or for writing the inequality. If \(n = 8\) not seen can still get (A2) for 2007. Answer \(n = 8\) with no working gets (G1).
OR
\(110 + n \times 10 > 176\) (A1)(M1)
\(n = 7\therefore {\text{year 2007}}\) (A1)(A1)(ft)(G2)[4 marks]
In (d) and (e) follow through from (c) if consistent wrong use of correct AP formula.
(i) \(180\) (A1)(ft)
Grove School gets the money. (A1)(ft)
Note: (A1) for \(180\) seen. (A1) for correct answer.
(ii) \({\text{100}} \times {\text{1}}{\text{.0}}{{\text{6}}^{n – 1}} > 110 + (n – 1) \times 10\) (M1)
\(n = 20\therefore {\text{year 2019}}\) (A1)(A1)(ft)(G2)
Note: (M1) for showing lists of values for each school and comparing them or for equating both formulae or writing the correct inequality. If \(n = 20\) not seen can still get (A2) for 2019. Follow through with ratio used in (b) and/or formula used in (d).
OR
\(100 \times {1.06^n} > 110 + n \times 10\) (M1)
\(n = 19\therefore {\text{year 2019}}\) (A1)(A1)(ft)(G2)
OR
graphically
Note: (M1) for sketch of both functions on the same graph, (A1) for the intersection point, (A1) for correct answer.[5 marks]
Question
The temperature in \(^ \circ {\text{C}}\) of a pot of water removed from the cooker is given by \(T(m) = 20 + 70 \times {2.72^{ – 0.4m}}\), where \(m\) is the number of minutes after the pot is removed from the cooker.
Show that the temperature of the water when it is removed from the cooker is \({90^ \circ }{\text{C}}\).[2]
The following table shows values for \(m\) and \(T(m)\).
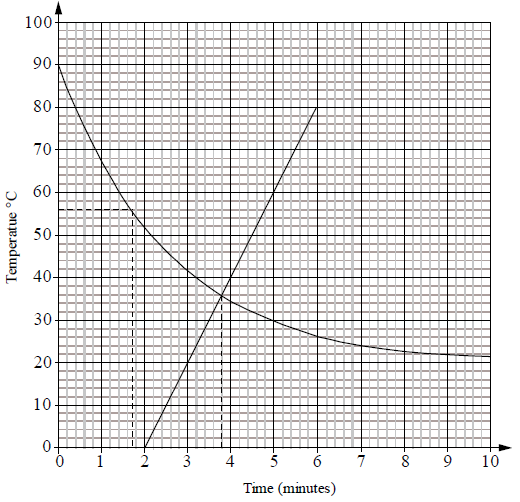
(i) Write down the value of \(s\).
(ii) Draw the graph of \(T(m)\) for \(0 \leqslant m \leqslant 10\) . Use a scale of \(1{\text{ cm}}\) to represent \(1\) minute on the horizontal axis and a scale of \(1{\text{ cm}}\) to represent \({10^ \circ }{\text{C}}\) on the vertical axis.
(iii) Use your graph to find how long it takes for the temperature to reach \({56^ \circ }{\text{C}}\). Show your method clearly.
(iv) Write down the temperature approached by the water after a long time. Justify your answer.[9]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
Draw the graph of \(S(m)\) on the same set of axes used for part (b).[2]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
Comment on the meaning of the constant \(20\) in the formula for \(S(m)\) in relation to the temperature of the soup.[1]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
(i) Use your graph to solve the equation \(S(m) = T(m)\) . Show your method clearly.
(ii) Hence describe by using inequalities the set of values of \(m\) for which \(S(m) > T(m)\).[4]
Answer/Explanation
Markscheme
\(T(0) = 20 + 70 \times {2.72^{ – 0.4 \times 0}} = 90\) (M1)(A1)(AG)
Note: (M1) for taking \(m = 0\) , (A1) for substituting \(0\) into the formula. For the A mark to be awarded \(90\) must be justified by correct method.[2 marks]
(i) 21.3 (A1)
(ii)
(A4)(ft)
Note: Scales and labels (A1). Smooth curve (A1). All points correct including the \(y\)-intercept (A2), 1 point incorrect (A1), otherwise (A0). Follow through from their value of \(s\).
(iii) \(m = 1.7{\text{ minutes}}\) (Accept \( \pm 0.2\) ) (A2)(ft)
Note: Follow through from candidate’s graph. Accept answers in minutes and seconds if consistent with graph. If answer incorrect and correct line(s) seen on graph award (M1)(A0).
(iv) \({20^ \circ }{\text{C}}\) (A1)(ft)
The curve behaves asymptotically to the line \(y = 20\) or similar. (A1)
OR
The room temperature is 20 or similar
OR
When \({\text{m}}\) is a very large number the term \(70 \times {2.72^{ – 0.4{\text{m}}}}\) tends to zero or similar.
Note: Follow through from their graph if appropriate.[9 marks]
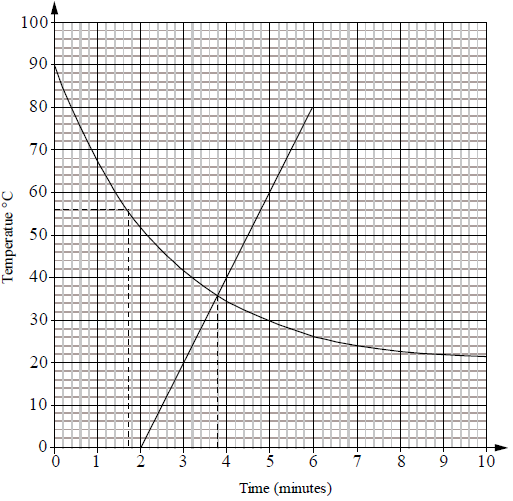(A1)(A1)
Notes: (A1) for correct line, (A1) for domain. If line not drawn on same set of axes award at most (A1)(A0).[2 marks]
It indicates by how much the temperature increases per minute. (A1)[1 mark]
(i) \(m = 3.8\) (Accept \( \pm 0.1\) ) (A2)(ft)
Note: Follow through from candidate’s graph. Accept answers in minutes and seconds if consistent with graph. If answer incorrect and correct line(s) seen on graph award (M1)(A0).
(ii) \(3.8 < m \leqslant 6\) (A1)(A1)(ft)
Note: (A1) for \(m > 3.8\) and (A1) for \(m \leqslant 6\). Follow through from candidate’s answer to part (e)(i). If candidate was already penalized in (c) for domain and does not state \(m \leqslant 6\) then award (A2)(ft).
Question
Consider the function \(f(x) = 3x + \frac{{12}}{{{x^2}}},{\text{ }}x \ne 0\).
Differentiate \(f (x)\) with respect to \(x\).[3]
Calculate \(f ′(x)\) when \(x = 1\).[2]
Use your answer to part (b) to decide whether the function, \(f\) , is increasing or decreasing at \(x = 1\). Justify your answer.[2]
Solve the equation \(f ′(x) = 0\).[3]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the coordinates of P.[2]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the gradient of T.[1]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the equation of T.[2]
Sketch the graph of the function f, for −3 ≤ x ≤ 6 and −7 ≤ y ≤ 15. Indicate clearly the point P and any intercepts of the curve with the axes.[4]
On your graph draw and label the tangent T.[2]
T intersects the graph of f at a second point. Write down the x-coordinate of this point of intersection.[1]
Answer/Explanation
Markscheme
\(f’ (x) = 3 – \frac{24}{x^3}\) (A1)(A1)(A1)
Note: Award (A1) for 3, (A1) for –24, (A1) for x3 (or x−3). If extra terms present award at most (A1)(A1)(A0).[3 marks]
\(f ‘(1) = -21\) (M1)(A1)(ft)(G2)
Note: (ft) from their derivative only if working seen.[2 marks]
Derivative (gradient, slope) is negative. Decreasing. (R1)(A1)(ft)
Note: Do not award (R0)(A1).[2 marks]
\(3 – \frac{{24}}{{{x^3}}} = 0\) (M1)
\(x^3 = 8\) (A1)
\(x = 2\) (A1)(ft)(G2)[3 marks]
(2, 9) (Accept x = 2, y = 9) (A1)(A1)(G2)
Notes: (ft) from their answer in (d).
Award (A1)(A0) if brackets not included and not previously penalized.[2 marks]
0 (A1)[1 mark]
y = 9 (A1)(A1)(ft)(G2)
Notes: Award (A1) for y = constant, (A1) for 9.
Award (A1)(ft) for their value of y in (e)(i).[2 marks]
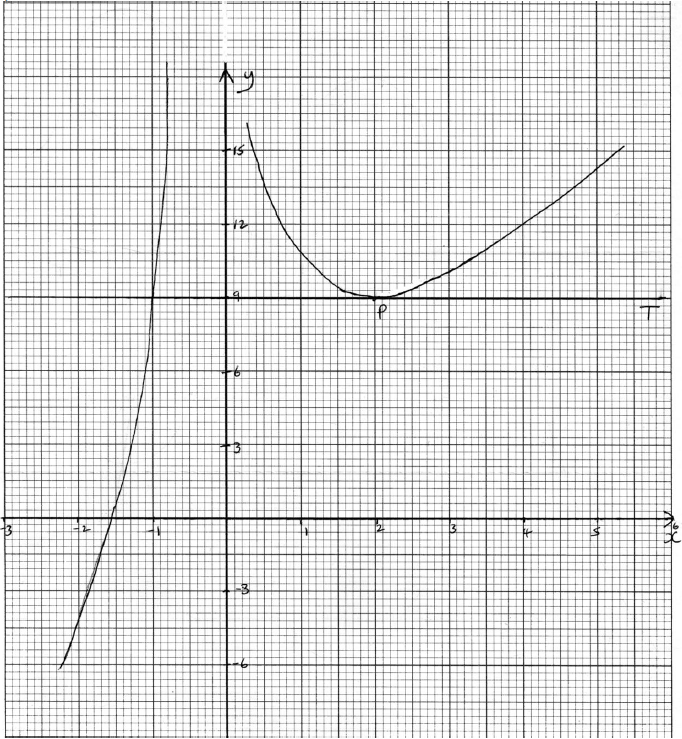(A4)
Notes: Award (A1) for labels and some indication of scale in the stated window.
Award (A1) for correct general shape (curve must be smooth and must not cross the y-axis).
Award (A1) for x-intercept seen in roughly the correct position.
Award (A1) for minimum (P).[4 marks]
Tangent drawn at P (line must be a tangent and horizontal). (A1)
Tangent labeled T. (A1)
Note: (ft) from their tangent equation only if tangent is drawn and answer is consistent with graph.[2 marks]
x = −1 (G1)(ft)[1 mark]
Question
A function is defined by \(f(x) = \frac{5}{{{x^2}}} + 3x + c,{\text{ }}x \ne 0,{\text{ }}c \in \mathbb{Z}\).
Write down an expression for \(f ′(x)\).[4]
Consider the graph of f. The graph of f passes through the point P(1, 4).
Find the value of c.[2]
There is a local minimum at the point Q.
Find the coordinates of Q.[4]
There is a local minimum at the point Q.
Find the set of values of x for which the function is decreasing.[3]
Let T be the tangent to the graph of f at P.
Show that the gradient of T is –7.[2]
Let T be the tangent to the graph of f at P.
Find the equation of T.[2]
T intersects the graph again at R. Use your graphic display calculator to find the coordinates of R.[2]
Answer/Explanation
Markscheme
\(f'(x) = \frac{{ – 10}}{{{x^3}}} + 3\) (A1)(A1)(A1)(A1)
Note: Award (A1) for −10, (A1) for x3 (or x−3), (A1) for 3, (A1) for no other constant term.[4 marks]
4 = 5 + 3 + c (M1)
Note: Award (M1) for substitution in f (x).
c = −4 (A1)(G2)[2 marks]
\(f ‘(x) = 0\) (M1)
\(0 = \frac{{ – 10}}{{{x^3}}} + 3\) (A1)(ft)
(1.49, 2.72) (accept x = 1.49 y = 2.72) (A1)(ft)(A1)(ft)(G3)
Notes: If answer is given as (1.5, 2.7) award (A0)(AP)(A1).
Award at most (M1)(A1)(A1)(A0) if parentheses not included. (ft) from their (a).
If no working shown award (G2)(G0) if parentheses are not included.
OR
Award (M2) for sketch, (A1)(ft)(A1)(ft) for correct coordinates. (ft) from their (b). (M2)(A1)(ft)(A1)(ft)
Note: Award at most (M2)(A1)(ft)(A0) if parentheses not included.[4 marks]
0 < x < 1.49 OR 0 < x ≤ 1.49 (A1)(A1)(ft)(A1)
Notes: Award (A1) for 0, (A1)(ft) for 1.49 and (A1) for correct inequality signs.
(ft) from their x value in (c) (i).[3 marks]
For P(1, 4) \(f ‘(1) = – 10 + 3\) (M1)(A1)
\(= -7\) (AG)
Note: Award (M1) for substituting \(x = 1\) into their \(f ‘(x)\). (A1) for \(-10 + 3\).
\(-7\) must be seen for (A1) to be awarded.[2 marks]
\(4 = -7 \times 1 + c\) \(11 = c\) (A1)
\(y = -7 x + 11\) (A1)[2 marks]
Point of intersection is R(−0.5, 14.5) (A1)(ft)(A1)(ft)(G2)(ft)
Notes: Award (A1) for the x coordinate, (A1) for the y coordinate.
Allow (ft) from candidate’s (d)(ii) equation and their (b) even with no working seen.
Award (A1)(ft)(A0) if brackets not included and not previously penalised.[2 marks]
Question
Sketch the graph of y = 2x for \( – 2 \leqslant x \leqslant 3\). Indicate clearly where the curve intersects the y-axis.[3]
Write down the equation of the asymptote of the graph of y = 2x.[2]
On the same axes sketch the graph of y = 3 + 2x − x2. Indicate clearly where this curve intersects the x and y axes.[3]
Using your graphic display calculator, solve the equation 3 + 2x − x2 = 2x.[2]
Write down the maximum value of the function f (x) = 3 + 2x − x2.[1]
Use Differential Calculus to verify that your answer to (e) is correct.[5]
The curve y = px2 + qx − 4 passes through the point (2, –10).
Use the above information to write down an equation in p and q.[2]
The gradient of the curve \(y = p{x^2} + qx – 4\) at the point (2, –10) is 1.
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
The gradient of the curve \(y = p{x^2} + qx – 4\) at the point (2, –10) is 1.
Hence, find a second equation in p and q.[1]
The gradient of the curve \(y = p{x^2} + qx – 4\) at the point (2, –10) is 1.
Solve the equations to find the value of p and of q.[3]
Answer/Explanation
Markscheme
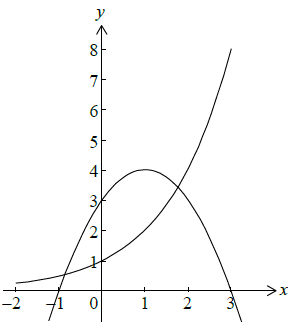(A1)(A1)(A1)
Note: Award (A1) for correct domain, (A1) for smooth curve, (A1) for y-intercept clearly indicated.[3 marks]
y = 0 (A1)(A1)
Note: Award (A1) for y = constant, (A1) for 0.[2 marks]
Note: Award (A1) for smooth parabola,
(A1) for vertex (maximum) in correct quadrant.
(A1) for all clearly indicated intercepts x = −1, x = 3 and y = 3.
The final mark is to be applied very strictly. (A1)(A1)(A1)[3 marks]
x = −0.857 x = 1.77 (G1)(G1)
Note: Award a maximum of (G1) if x and y coordinates are both given.[2 marks]
4 (G1)
Note: Award (G0) for (1, 4).[1 mark]
\(f'(x) = 2 – 2x\) (A1)(A1)
Note: Award (A1) for each correct term.
Award at most (A1)(A0) if any extra terms seen.
\(2 – 2x = 0\) (M1)
Note: Award (M1) for equating their gradient function to zero.
\(x = 1\) (A1)(ft)
\(f (1) = 3 + 2(1) – (1)^2 = 4\) (A1)
Note: The final (A1) is for substitution of x = 1 into \(f (x)\) and subsequent correct answer. Working must be seen for final (A1) to be awarded.[5 marks]
22 × p + 2q − 4 = −10 (M1)
Note: Award (M1) for correct substitution in the equation.
4p + 2q = −6 or 2p + q = −3 (A1)
Note: Accept equivalent simplified forms.[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 2px + q\) (A1)(A1)
Note: Award (A1) for each correct term.
Award at most (A1)(A0) if any extra terms seen.[2 marks]
4p + q = 1 (A1)(ft)[1 mark]
4p + 2q = −6
4p + q = 1 (M1)
Note: Award (M1) for sensible attempt to solve the equations.
p = 2, q = −7 (A1)(A1)(ft)(G3)[3 marks]
Question
Daniel wants to invest \(\$ 25\,000\) for a total of three years. There are two investment options.
Option One pays compound interest at a nominal annual rate of interest of 5 %, compounded annually.
Option Two pays compound interest at a nominal annual rate of interest of 4.8 %, compounded monthly.
An arithmetic sequence is defined as
un = 135 + 7n, n = 1, 2, 3, …
Calculate the value of his investment at the end of the third year for each investment option, correct to two decimal places.[8]
Determine Daniel’s best investment option.[1]
Calculate u1, the first term in the sequence.[2]
Show that the common difference is 7.[2]
Sn is the sum of the first n terms of the sequence.
Find an expression for Sn. Give your answer in the form Sn = An2 + Bn, where A and B are constants.[3]
The first term, v1, of a geometric sequence is 20 and its fourth term v4 is 67.5.
Show that the common ratio, r, of the geometric sequence is 1.5.[2]
Tn is the sum of the first n terms of the geometric sequence.
Calculate T7, the sum of the first seven terms of the geometric sequence.[2]
Tn is the sum of the first n terms of the geometric sequence.
Use your graphic display calculator to find the smallest value of n for which Tn > Sn.[2]
Answer/Explanation
Markscheme
Option 1: Amount \( = 25\,000{\left( {1 + \frac{5}{{100}}} \right)^3}\) (M1)(A1)
= \(28\,940.63\) (A1)(G2)
Note: Award (M1) for substitution in compound interest formula, (A1) for correct substitution. Give full credit for use of lists.
Option 2: Amount \( = 25\,000{\left( {1 + \frac{{4.8}}{{12(100)}}} \right)^{3 \times 12}}\) (M1)
= \(28\,863.81\) (A1)(G2)
Note: Award (M1) for correct substitution in the compound interest formula. Give full credit for use of lists.[8 marks]
Option 1 is the best investment option. (A1)(ft)[1 mark]
u1 = 135 + 7(1) (M1)
= 142 (A1)(G2)[2 marks]
u2 = 135 + 7(2) = 149 (M1)
d = 149 – 142 OR alternatives (M1)(ft)
d = 7 (AG)[2 marks]
\({S_n} = \frac{{n[2(142) + 7(n – 1)]}}{2}\) (M1)(ft)
Note: Award (M1) for correct substitution in correct formula.
\( = \frac{{n[277 + 7n]}}{2}\) OR equivalent (A1)
\( = \frac{{7{n^2}}}{2} + \frac{{277n}}{2}\) (= 3.5n2 + 138.5n) (A1)(G3)[3 marks]
20r3 = 67.5 (M1)
r3 = 3.375 OR \(r = \sqrt[3]{{3.375}}\) (A1)
r = 1.5 (AG)[2 marks]
\({T_7} = \frac{{20({{1.5}^7} – 1)}}{{(1.5 – 1)}}\) (M1)
Note: Award (M1) for correct substitution in correct formula.
= 643 (accept 643.4375) (A1)(G2)[2 marks]
\(\frac{{20({{1.5}^n} – 1)}}{{(1.5 – 1)}} > \frac{{7{n^2}}}{2} + \frac{{277n}}{2}\) (M1)
Note: Award (M1) for an attempt using lists or for relevant graph.
n = 10 (A1)(ft)(G2)
Note: Follow through from their (c).[2 marks]
Question
Give all answers in this question to the nearest whole currency unit.
Ying and Ruby each have 5000 USD to invest.
Ying invests his 5000 USD in a bank account that pays a nominal annual interest rate of 4.2 % compounded yearly. Ruby invests her 5000 USD in an account that offers a fixed interest of 230 USD each year.
Find the amount of money that Ruby will have in the bank after 3 years.[2]
Show that Ying will have 7545 USD in the bank at the end of 10 years.[3]
Find the number of complete years it will take for Ying’s investment to first exceed 6500 USD.[3]
Find the number of complete years it will take for Ying’s investment to exceed Ruby’s investment.[3]
Ruby moves from the USA to Italy. She transfers 6610 USD into an Italian bank which has an exchange rate of 1 USD = 0.735 Euros. The bank charges 1.8 % commission.
Calculate the amount of money Ruby will invest in the Italian bank after commission.[4]
Ruby returns to the USA for a short holiday. She converts 800 Euros at a bank in Chicago and receives 1006.20 USD. The bank advertises an exchange rate of 1 Euro = 1.29 USD.
Calculate the percentage commission Ruby is charged by the bank.[5]
Answer/Explanation
Markscheme
5000 + 3 × 230 = 5690 (M1)(A1)(G2)
Note: Accept alternative method.[2 marks]
\({\text{A}} = 5000{\left( {1 + \frac{{4.2}}{{100}}} \right)^{10}}\) or equivalent (M1)(A1)
\( = 7544.79 \ldots \) (A1)
\( = 7545{\text{ USD}}\) (AG)
Note: Award (M1) for correct substituted compound interest formula, (A1) for correct substitutions, (A1) for unrounded answer seen.
If final line not seen award at most (M1)(A1)(A0).[3 marks]
5000(1.042)n > 6500 (M1)(A1)
Notes: Award (M1) for setting up correct equation/inequality, (A1) for correct values.
Follow through from their formula in part (b).
OR
List of values seen with at least 2 terms (M1)
Lists of values including at least the terms with n = 6 and n = 7 (A1)
Note: Follow through from their formula in part (b).
OR
Sketch showing 2 graphs, one exponential, the other a horizontal line (M1)
Point of intersection identified or vertical line (M1)
Note: Follow through from their formula in part (b).
n = 7 (A1)(ft)(G2)[3 marks]
5000(1.042)n > 5000 + 230n (M1)(A1)
Note: Award (M1) for setting up correct equation/inequality, (A1) for correct values.
OR
2 lists of values seen (at least 2 terms per list) (M1)
Lists of values including at least the terms with n = 5 and n = 6 (A1)
Note: One of the lists may be written under (c).
OR
Sketch showing 2 graphs of correct shape (M1)
Point of intersection identified or vertical line (M1)
n = 6 (A1)(ft)(G2)
Note: Follow through from their formulae used in parts (a) and (b).[3 marks]
6610 × 0.735 (M1)
= 4858.35 (A1)
4858.35 × 0.982(= 4770.8997…) (M1)
= 4771 Euros (A1)(ft)(G3)
Note: Accept alternative method.[4 marks]
800 × 1.29 (= 1032 USD) (M1)(A1)
Note: Award (M1) for multiplying by 1.29, (A1) for 1032. Award (G2) for 1032 if product not seen.
(1032 – 1006.20 = 25.8)
\(25.8 \times \frac{100}{1032} \%\) (A1)(M1)
Note: Award (A1) for 25.8 seen, (M1) for multiplying by \(\frac{100}{1032}\).
OR
\(\frac{1006.20}{1032} = 0.975\) (M1)(A1)
OR
\(\frac{1006.20}{1032} \times 100 = 97.5\) (M1)(A1)
\( = 2.5{\text{ }}\% \) (A1)(G3)
Notes: If working not shown award (G3) for 2.5.
Accept alternative method.[5 marks]
Question
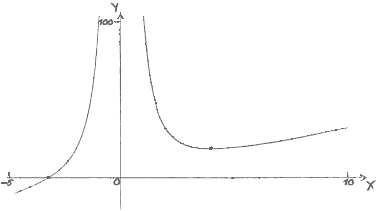
The diagram shows part of the graph of \(f(x) = {x^2} – 2x + \frac{9}{x}\) , where \(x \ne 0\) .
Write down
(i) the equation of the vertical asymptote to the graph of \(y = f (x)\) ;
(ii) the solution to the equation \(f (x) = 0\) ;
(iii) the coordinates of the local minimum point.[5]
Find \(f'(x)\) .[4]
Show that \(f'(x)\) can be written as \(f'(x) = \frac{{2{x^3} – 2{x^2} – 9}}{{{x^2}}}\) .[2]
Find the gradient of the tangent to \(y = f (x)\) at the point \({\text{A}}(1{\text{, }}8)\) .[2]
The line, \(L\), passes through the point A and is perpendicular to the tangent at A.
Write down the gradient of \(L\) .[1]
The line, \(L\) , passes through the point A and is perpendicular to the tangent at A.
Find the equation of \(L\) . Give your answer in the form \(y = mx + c\) .[3]
The line, \(L\) , passes through the point A and is perpendicular to the tangent at A.
\(L\) also intersects the graph of \(y = f (x)\) at points B and C . Write down the x-coordinate of B and of C .[2]
Answer/Explanation
Markscheme
(i) \(x = 0\) (A1)(A1)
Note: Award (A1) for \(x = \) a constant, (A1) for the constant in their equation being \(0\).
(ii) \( – 1.58\) (\( – 1.58454 \ldots \)) (G1)
Note: Accept \( – 1.6\), do not accept \( – 2\) or \( – 1.59\).
(iii) \((2.06{\text{, }}4.49)\) \((2.06020 \ldots {\text{, }}4.49253 \ldots )\) (G1)(G1)
Note: Award at most (G1)(G0) if brackets not used. Award (G0)(G1)(ft) if coordinates are reversed.
Note: Accept \(x = 2.06\), \(y = 4.49\) .
Note: Accept \(2.1\), do not accept \(2.0\) or \(2\). Accept \(4.5\), do not accept \(5\) or \(4.50\).[5 marks]
\(f'(x) = 2x – 2 – \frac{9}{{{x^2}}}\) (A1)(A1)(A1)(A1)
Notes: Award (A1) for \(2x\), (A1) for \( – 2\), (A1) for \( – 9\), (A1) for \({x^{ – 2}}\) . Award a maximum of (A1)(A1)(A1)(A0) if there are extra terms present.[4 marks]
\(f'(x) = \frac{{{x^2}(2x – 2)}}{{{x^2}}} – \frac{9}{{{x^2}}}\) (M1)
Note: Award (M1) for taking the correct common denominator.
\( = \frac{{(2{x^3} – 2{x^2})}}{{{x^2}}} – \frac{9}{{{x^2}}}\) (M1)
Note: Award (M1) for multiplying brackets or equivalent.
\( = \frac{{2{x^3} – 2{x^2} – 9}}{{{x^2}}}\) (AG)
Note: The final (M1) is not awarded if the given answer is not seen.[2 marks]
\(f'(1) = \frac{{2{{(1)}^3} – 2(1) – 9}}{{{{(1)}^2}}}\) (M1)
\( = – 9\) (A1)(G2)
Note: Award (M1) for substitution into given (or their correct) \(f'(x)\) . There is no follow through for use of their incorrect derivative.[2 marks]
\(\frac{1}{9}\) (A1)(ft)
Note: Follow through from part (d).[1 mark]
\(y – 8 = \frac{1}{9}(x – 1)\) (M1)(M1)
Notes: Award (M1) for substitution of their gradient from (e), (M1) for substitution of given point. Accept all forms of straight line.
\(y = \frac{1}{9}x + \frac{{71}}{9}\) (\(y = 0.111111 \ldots x + 7.88888 \ldots \)) (A1)(ft)(G3)
Note: Award the final (A1)(ft) for a correctly rearranged formula of their straight line in (f). Accept \(0.11x\), do not accept \(0.1x\). Accept \(7.9\), do not accept \(7.88\), do not accept \(7.8\).[3 marks]
\( – 2.50\), \(3.61\) (\( – 2.49545 \ldots \), \(3.60656 \ldots \)) (A1)(ft)(A1)(ft)
Notes: Follow through from their line \(L\) from part (f) even if no working shown. Award at most (A0)(A1)(ft) if their correct coordinate pairs given.
Note: Accept \( – 2.5\), do not accept \( – 2.49\). Accept \(3.6\), do not accept \(3.60\).[2 marks]
Question
Consider the function \(f(x) = – \frac{1}{3}{x^3} + \frac{5}{3}{x^2} – x – 3\).
Sketch the graph of y = f (x) for −3 ≤ x ≤ 6 and −10 ≤ y ≤ 10 showing clearly the axes intercepts and local maximum and minimum points. Use a scale of 2 cm to represent 1 unit on the x-axis, and a scale of 1 cm to represent 1 unit on the y-axis.[4]
Find the value of f (−1).[2]
Write down the coordinates of the y-intercept of the graph of f (x).[1]
Find f ‘(x).[3]
Show that \(f'( – 1) = – \frac{{16}}{3}\).[1]
Explain what f ‘(−1) represents.[2]
Find the equation of the tangent to the graph of f (x) at the point where x is –1.[2]
Sketch the tangent to the graph of f (x) at x = −1 on your diagram for (a).[2]
P and Q are points on the curve such that the tangents to the curve at these points are horizontal. The x-coordinate of P is a, and the x-coordinate of Q is b, b > a.
Write down the value of
(i) a ;
(ii) b .[2]
P and Q are points on the curve such that the tangents to the curve at these points are horizontal. The x-coordinate of P is a, and the x-coordinate of Q is b, b > a.
Describe the behaviour of f (x) for a < x < b.[1]
Answer/Explanation
Markscheme
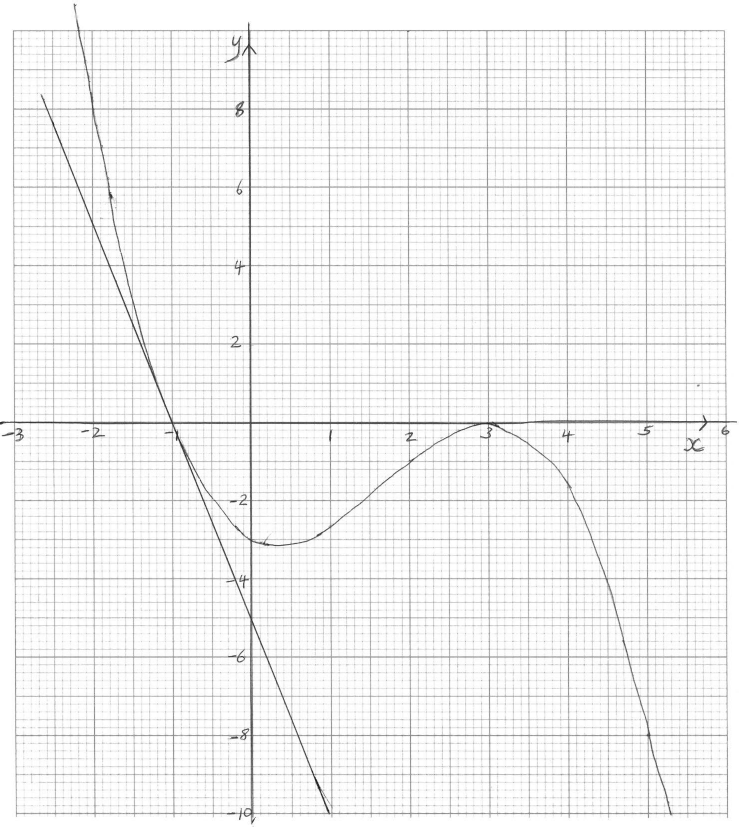
(A1) for indication of window and labels. (A1) for smooth curve that does not enter the first quadrant, the curve must consist of one line only.
(A1) for x and y intercepts in approximately correct positions (allow ±0.5).
(A1) for local maximum and minimum in approximately correct position. (minimum should be 0 ≤ x ≤ 1 and –2 ≤ y ≤ –4 ), the y-coordinate of the maximum should be 0 ± 0.5. (A4)[4 marks]
\(-\frac{1}{3}(-1)^3 + \frac{5}{3}(-1)^2 – (-1) – 3 \) (M1)
Note: Award (M1) for substitution of –1 into f (x)
= 0 (A1)(G2)[2 marks]
(0, –3) (A1)
OR
x = 0, y = –3 (A1)
Note: Award (A0) if brackets are omitted.[1 mark]
\(f'(x) = – {x^2} + \frac{{10}}{3}x – 1\) (A1)(A1)(A1)
Note: Award (A1) for each correct term. Award (A1)(A1)(A0) at most if there are extra terms.[3 marks]
\(f'( – 1) = – {( – 1)^2} + \frac{{10}}{3}( – 1) – 1\) (M1)
\(= -\frac{16}{3}\) (AG)
Note: Award (M1) for substitution of x = –1 into correct derivative only. The final answer must be seen.[1 mark]
f ‘(–1) gives the gradient of the tangent to the curve at the point with x = –1. (A1)(A1)
Note: Award (A1) for “gradient (of curve)”, (A1) for “at the point with x = –1”. Accept “the instantaneous rate of change of y” or “the (first) derivative”.[2 marks]
\(y = – \frac{16}{3} x + c\) (M1)
Note: Award (M1) for \(-\frac{16}{3}\) substituted in equation.
\(0 = – \frac{16}{3} \times (-1) + c \)
\(c = – \frac{16}{3}\)
\(y = – \frac{{16}}{3}x – \frac{{16}}{3}\) (A1)(G2)
Note: Accept y = –5.33x – 5.33.
OR
\((y – 0) = \frac{{-16}}{3}(x + 1)\) (M1)(A1)(G2)
Note: Award (M1) for \( – \frac{{16}}{3}\) substituted in equation, (A1) for correct equation. Follow through from their answer to part (b). Accept y = –5.33 (x +1). Accept equivalent equations.[2 marks]
(A1)(ft) for a tangent to their curve drawn.
(A1)(ft) for their tangent drawn at the point x = –1. (A1)(ft)(A1)(ft)
Note: Follow through from their graph. The tangent must be a straight line otherwise award at most (A0)(A1).
[2 marks]
(i) \(a = \frac{1}{3}\) (G1
(ii) \(b = 3\) (G1)
Note: If a and b are reversed award (A0)(A1).[2 marks]
f (x) is increasing (A1)[1 mark]
Question
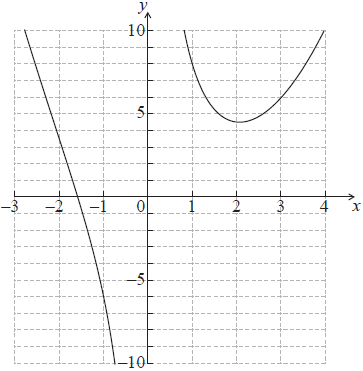
Consider the function \(g(x) = bx – 3 + \frac{1}{{{x^2}}},{\text{ }}x \ne 0\).
Write down the equation of the vertical asymptote of the graph of y = g(x) .[2]
Write down g′(x) .[3]
The line T is the tangent to the graph of y = g(x) at the point where x = 1. The gradient of T is 3.
Show that b = 5.[2]
The line T is the tangent to the graph of y = g(x) at the point where x = 1. The gradient of T is 3.
Find the equation of T.[3]
Using your graphic display calculator find the coordinates of the point where the graph of y = g(x) intersects the x-axis.[2]
(i) Sketch the graph of y = g(x) for −2 ≤ x ≤ 5 and −15 ≤ y ≤ 25, indicating clearly your answer to part (e).
(ii) Draw the line T on your sketch.[6]
Using your graphic display calculator find the coordinates of the local minimum point of y = g(x) .[2]
Write down the interval for which g(x) is increasing in the domain 0 < x < 5 .[2]
Answer/Explanation
Markscheme
x = 0 (A1)(A1)
Notes: Award (A1) for x=constant, (A1) for 0. Award (A0)(A0) if answer is not an equation.[2 marks]
\(b – \frac{2}{{{x^3}}}\) (A1)(A1)(A1)
Note: Award (A1) for b, (A1) for −2, (A1) for \(\frac{1}{{{x^3}}}\) (or x−3). Award at most (A1)(A1)(A0) if extra terms seen.[3 marks]
\(3 = b – \frac{2}{{{{(1)}^3}}}\) (M1)(M1)
Note: Award (M1) for substituting 1 into their gradient function, (M1) for equating their gradient function to 3.
b = 5 (AG)
Note: Award at most (M1)(A0) if final line is not seen or b does not equal 5.[2 marks]
g(1) = 3 or (1, 3) (seen or implied from the line below) (A1)
3 = 3 × 1 + c (M1)
Note: Award (M1) for correct substitution of their point (1, 3) and gradient 3 into equation y = mx + c. Follow through from their point of tangency.
y = 3x (A1)(ft)(G2)
OR
y − 3 = 3(x − 1) (M1)(A1)(ft)(G2)
Note: Award (M1) for substitution of gradient 3 and their point (1, 3) into y − y1 = m(x − x1), (A1)(ft) for correct substitutions. Follow through from their point of tangency. Award at most (A1)(M1)(A0)(ft) if further incorrect working seen.[3 marks]
(−0.439, 0) ((−0.438785…, 0)) (G1)(G1)
Notes: If no parentheses award at most (G1)(G0). Accept x = 0.439, y = 0.[2 marks]
(i)
Award (A1) for labels and some indication of scale in the stated window.
Award (A1) for correct general shape (curve must be smooth and must not cross the y-axis)
Award (A1)(ft) for x-intercept consistent with their part (e).
Award (A1) for local minimum in the first quadrant. (A1)(A1)(A1)(ft)(A1)
(ii) Tangent to curve drawn at approximately x = 1 (A1)(A1)
Note: Award (A1) for a line tangent to curve approximately at x = 1. Must be a straight line for the mark to be awarded. Award (A1)(ft) for line passing through the origin. Follow through from their answer to part (d).[6 marks]
(0.737, 2.53) ((0.736806…, 2.52604…)) (G1)(G1)
Notes: Do not penalize for lack of parentheses if already penalized in (e). Accept x = 0.737, y = 2.53.[2 marks]
0.737 < x < 5 OR (0.737;5) (A1)(A1)(ft)
Notes: Award (A1) for correct strict or weak inequalities with x seen if the interval is given as inequalities, (A1)(ft) for 0.737 and 5 or their value from part (g).[2 marks]
Question
On Monday Paco goes to a running track to train. He runs the first lap of the track in 120 seconds. Each lap Paco runs takes him 10 seconds longer than his previous lap.
Find the time, in seconds, Paco takes to run his fifth lap.[3]
Paco runs his last lap in 260 seconds.
Find how many laps he has run on Monday.[3]
Find the total time, in minutes, run by Paco on Monday.[4]
On Wednesday Paco takes Lola to train. They both run the first lap of the track in 120 seconds. Each lap Lola runs takes 1.06 times as long as her previous lap.
Find the time, in seconds, Lola takes to run her third lap.[3]
Find the total time, in seconds, Lola takes to run her first four laps.[3]
Each lap Paco runs again takes him 10 seconds longer than his previous lap. After a certain number of laps Paco takes less time per lap than Lola.
Find the number of the lap when this happens.[3]
Answer/Explanation
Markscheme
\(120 + 10 \times 4\) (M1)(A1)
Notes: Award (M1) for substituted AP formula, (A1) for correct substitutions. Accept a list of 4 correct terms.
= 160 (A1)(G3)
\(120 + (n – 1) \times 10 = 260\) (M1)(M1)
Notes: Award (M1) for correctly substituted AP formula, (M1) for equating to 260. Accept a list of correct terms showing at least the 14th and 15th terms.
= 15 (A1)(G2)
\(\frac{{15}}{2}(120 + 260)\) or \(\frac{{15}}{2}(2 \times 120 + (15 – 1) \times 10)\) (M1)(A1)(ft)
Notes: Award (M1) for substituted AP sum formula, (A1)(ft) for correct substitutions. Accept a sum of a list of 15 correct terms. Follow through from their answer to part (b).
2850 seconds (A1)(ft)(G2)
Note: Award (G2) for 2850 seen with no working shown.
47.5 minutes (A1)(ft)(G3)
Notes: A final (A1)(ft) can be awarded for correct conversion from seconds into minutes of their incorrect answer. Follow through from their answer to part (b).
\(120 \times {1.06^{3 – 1}}\) (M1)(A1)
Notes: Award (M1) for substituted GP formula, (A1) for correct substitutions. Accept a list of 3 correct terms.
= 135 (134.832) (A1)(G2)
\({S_4} = \frac{{120({{1.06}^4} – 1)}}{{(1.06 – 1)}}\) (M1)(A1)
Notes: Award (M1) for substituted GP sum formula, (A1) for correct substitutions. Accept a sum of a list of 4 correct terms.
= 525 (524.953…) (A1)(G2)
\(120 + (n – 1) \times 10 < 120 \times {1.06^{n – 1}}\) (M1)(M1)
Notes: Award (M1) for correct left hand side, (M1) for correct right hand side. Accept an equation. Follow through from their expressions given in parts (a) and (d).
OR
List of at least 2 terms for both sequences (120, 130, … and 120, 127.2, …) (M1)
List of correct 12th and 13th terms for both sequences (…, 230, 240 and …, 227.8, 241.5) (M1)
OR
A sketch with a line and an exponential curve, (M1)
An indication of the correct intersection point (M1)
13th lap (A1)(ft)(G2)
Note: Do not award the final (A1)(ft) if final answer is not a positive integer.
Question
The diagram shows an aerial view of a bicycle track. The track can be modelled by the quadratic function
\(y = \frac{{ – {x^2}}}{{10}} + \frac{{27}}{2}x\), where \(x \geqslant 0,{\text{ }}y \geqslant 0\)
(x , y) are the coordinates of a point x metres east and y metres north of O , where O is the origin (0, 0) . B is a point on the bicycle track with coordinates (100, 350) .
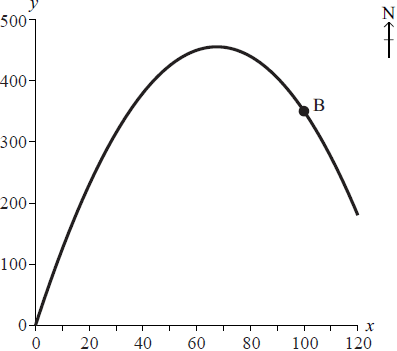
The coordinates of point A are (75, 450). Determine whether point A is on the bicycle track. Give a reason for your answer.[3]
Find the derivative of \(y = \frac{{ – {x^2}}}{{10}} + \frac{{27}}{2}x\).[2]
Use the answer in part (b) to determine if A (75, 450) is the point furthest north on the track between O and B. Give a reason for your answer.[4]
(i) Write down the midpoint of the line segment OB.
(ii) Find the gradient of the line segment OB.[3]
Scott starts from a point C(0,150) . He hikes along a straight road towards the bicycle track, parallel to the line segment OB.
Find the equation of Scott’s road. Express your answer in the form \(ax + by = c\), where \(a, b {\text{ and }} c \in \mathbb{R}\).[3]
Use your graphic display calculator to find the coordinates of the point where Scott first crosses the bicycle track.[2]
Answer/Explanation
Markscheme
\(y = – \frac{{{{75}^2}}}{{10}} + \frac{{27}}{2} \times 75\) (M1)
Note: Award (M1) for substitution of 75 in the formula of the function.
= 450 (A1)
Yes, point A is on the bike track. (A1)
Note: Do not award the final (A1) if correct working is not seen.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{2x}}{{10}} + \frac{{27}}{2}\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 0.2x + 13.5} \right)\) (A1)(A1)
Notes: Award (A1) for each correct term. If extra terms are seen award at most (A1)(A0). Accept equivalent forms.
\( – \frac{{2x}}{{10}} + \frac{{27}}{2} = 0\) (M1)
Note: Award (M1) for equating their derivative from part (b) to zero.
\(x = 67.5\) (A1)(ft)
Note: Follow through from their derivative from part (b).
\( {\text{(Their) }} 67.5 \ne 75\) (R1)
Note: Award (R1) for a comparison of their 67.5 with 75. Comparison may be implied (eg 67.5 is the x-coordinate of the furthest north point).
OR
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{2 \times (75)}}{{10}} + \frac{{27}}{2}\) (M1)
Note: Award (M1) for substitution of 75 into their derivative from part (b).
\(= -1.5\) (A1)(ft)
Note: Follow through from their derivative from part (b).
\({\text{(Their)}} -1.5 \ne 0\) (R1)
Note: Award (R1) for a comparison of their –1.5 with 0. Comparison may be implied (eg The gradient of the parabola at the furthest north point (vertex) is 0).
Hence A is not the furthest north point. (A1)(ft)
Note: Do not award (R0)(A1)(ft). Follow through from their derivative from part (b).
(i) M(50,175) (A1)
Note: If parentheses are omitted award (A0). Accept x = 50, y = 175.
(ii) \(\frac{{350 – 0}}{{100 – 0}}\) (M1)
Note: Award (M1) for correct substitution in gradient formula.
\( = 3.5\left( {\frac{{350}}{{100}},\frac{7}{2}} \right)\) (A1)(ft)(G2)
Note: Follow through from (d)(i) if midpoint is used to calculate gradient. Award (G1)(G0) for answer 3.5x without working.
\(y = 3.5x + 150\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for using their gradient from part (d), (A1)(ft) for correct equation of line.
\(3.5x – y = -150\) or \(7x – 2y = -300\) (or equivalent) (A1)(ft)
Note: Award (A1)(ft) for expressing their equation in the form \(ax + by = c\).
(18.4, 214) (18.3772…, 214.320…) (A1)(ft)(A1)(ft)(G2)(ft)
Notes: Follow through from their equation in (e). Coordinates must be positive for follow through marks to be awarded. If parentheses are omitted and not already penalized in (d)(i) award at most (A0)(A1)(ft). If coordinates of the two intersection points are given award (A0)(A1)(ft). Accept x = 18.4, y = 214.
Question
Consider the sequence \({u_1},{\text{ }}{u_2},{\text{ }}{u_3},{\text{ }} \ldots ,{\text{ }}{{\text{u}}_n},{\text{ }} \ldots \) where
\[{u_1} = 600,{\text{ }}{u_2} = 617,{\text{ }}{u_3} = 634,{\text{ }}{u_4} = 651.\]
The sequence continues in the same manner.
Find the value of \({u_{20}}\).[3]
Find the sum of the first 10 terms of the sequence.[3]
Now consider the sequence \({v_1},{\text{ }}{v_2},{\text{ }}{v_3},{\text{ }} \ldots ,{\text{ }}{v_n},{\text{ }} \ldots \) where
\[{v_1} = 3,{\text{ }}{v_2} = 6,{\text{ }}{v_3} = 12,{\text{ }}{v_4} = 24\]
This sequence continues in the same manner.
Find the exact value of \({v_{10}}\).[3]
Now consider the sequence \({v_1},{\text{ }}{v_2},{\text{ }}{v_3},{\text{ }} \ldots ,{\text{ }}{v_n},{\text{ }} \ldots \) where
\[{v_1} = 3,{\text{ }}{v_2} = 6,{\text{ }}{v_3} = 12,{\text{ }}{v_4} = 24\]
This sequence continues in the same manner.
Find the sum of the first 8 terms of this sequence.[3]
\(k\) is the smallest value of \(n\) for which \({v_n}\) is greater than \({u_n}\).
Calculate the value of \(k\).[3]
Answer/Explanation
Markscheme
\(600 + (20 – 1) \times 17\) (M1)(A1)
Note: Award (M1) for substituted arithmetic sequence formula, (A1) for correct substitutions. If a list is used, award (M1) for at least 6 correct terms seen, award (A1) for at least 20 correct terms seen.
\( = 923\) (A1)(G3)[3 marks]
\(\frac{{10}}{2}\left[ {2 \times 600 + (10 – 1) \times 17} \right]\) (M1)(A1)
Note: Award (M1) for substituted arithmetic series formula, (A1) for their correct substitutions. Follow through from part (a). For consistent use of geometric series formula in part (b) with the geometric sequence formula in part (a) award a maximum of (M1)(A1)(A0) since their final answer cannot be an integer.
OR
\({u_{10}} = 600 + (10 – 1)17 = 753\) (M1)
\({S_{10}} = \frac{{10}}{2}\left( {600 + {\text{their }}{u_{10}}} \right)\) (M1)
Note: Award (M1) for their correctly substituted arithmetic sequence formula, (M1) for their correctly substituted arithmetic series formula. Follow through from part (a) and within part (b).
Note: If a list is used, award (M1) for at least 10 correct terms seen, award (A1) for these terms being added.
\( = 6765\) (accept \(6770\)) (A1)(ft)(G2)[3 marks]
\(3 \times {2^9}\) (M1)(A1)
Note: Award (M1) for substituted geometric sequence formula, (A1) for correct substitutions. If a list is used, award (M1) for at least 6 correct terms seen, award (A1) for at least 8 correct terms seen.
\( = 1536\) (A1)(G3)
Note: Exact answer only. If both exact and rounded answer seen, award the final (A1).[3 marks]
\(\frac{{3 \times \left( {{2^8} – 1} \right)}}{{2 – 1}}\) (M1)(A1)(ft)
Note: Award (M1) for substituted geometric series formula, (A1) for their correct substitutions. Follow through from part (c). If a list is used, award (M1) for at least 8 correct terms seen, award (A1) for these 8 correct terms being added. For consistent use of arithmetic series formula in part (d) with the arithmetic sequence formula in part (c) award a maximum of (M1)(A1)(A1).
\( = 765\) (A1)(ft)(G2)[3 marks]
\(3 \times {2^{k – 1}} > 600 + (k – 1)(17)\) (M1)
Note: Award (M1) for their correct inequality; allow equation.
Follow through from parts (a) and (c). Accept sketches of the two functions as a valid method.
\(k > 8.93648 \ldots \) (may be implied) (A1)(ft)
Note: Award (A1) for \(8.93648…\) seen. The GDC gives answers of \(-34.3\) and \(8.936\) to the inequality; award (M1)(A1) if these are seen with working shown.
OR
\({v_8} = 384\) \({u_8} = 719\) (M1)
\({v_9} = 768\) \({u_9} = 736\) (M1)
Note: Award (M1) for \({v_8}\) and \({u_8}\) both seen, (M1) for \({v_9}\) and \({u_9}\) both seen.
\(k = 9\) (A1)(ft)(G2)
Note: Award (G1) for \(8.93648…\) and \(-34.3\) seen as final answer without working. Accept use of \(n\).[3 marks]
Question
Consider the function \(f(x) = \frac{{96}}{{{x^2}}} + kx\), where \(k\) is a constant and \(x \ne 0\).
Write down \(f'(x)\).[3]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Show that \(k = 3\).[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f(2)\).[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f'(2)\)[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find the equation of the normal to the graph of \(y = f(x)\) at the point where \(x = 2\).
Give your answer in the form \(ax + by + d = 0\) where \(a,{\text{ }}b,{\text{ }}d \in \mathbb{Z}\).[3]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Sketch the graph of \(y = f(x)\), for \( – 5 \leqslant x \leqslant 10\) and \( – 10 \leqslant y \leqslant 100\).[4]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Write down the coordinates of the point where the graph of \(y = f(x)\) intersects the \(x\)-axis.[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
State the values of \(x\) for which \(f(x)\) is decreasing.[2]
Answer/Explanation
Markscheme
\(\frac{{ – 192}}{{{x^3}}} + k\) (A1)(A1)(A1)
Note: Award (A1) for \(-192\), (A1) for \({x^{ – 3}}\), (A1) for \(k\) (only).
at local minimum \(f'(x) = 0\) (M1)
Note: Award (M1) for seeing \(f'(x) = 0\) (may be implicit in their working).
\(\frac{{ – 192}}{{{4^3}}} + k = 0\) (A1)
\(k = 3\) (AG)
Note: Award (A1) for substituting \(x = 4\) in their \(f'(x) = 0\), provided it leads to \(k = 3\). The conclusion \(k = 3\) must be seen for the (A1) to be awarded.
\(\frac{{96}}{{{2^2}}} + 3(2)\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in \(f(x)\).
\( = 30\) (A1)(G2)
\(\frac{{ – 192}}{{{2^3}}} + 3\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in their \(f'(x)\).
\( = – 21\) (A1)(ft)(G2)
Note: Follow through from part (a).
\(y – 30 = \frac{1}{{21}}(x – 2)\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for their \(\frac{1}{{21}}\) seen, (M1) for the correct substitution of their point and their normal gradient in equation of a line.
Follow through from part (c) and part (d).
OR
gradient of normal \( = \frac{1}{{21}}\) (A1)(ft)
\(30 = \frac{1}{{21}} \times 2 + c\) (M1)
\(c = 29\frac{{19}}{{21}}\)
\(y = \frac{1}{{21}}x + 29\frac{{19}}{{21}}\;\;\;(y = 0.0476x + 29.904)\)
\(x – 21y + 628 = 0\) (A1)(ft)(G2)
Notes: Accept equivalent answers.
(A1)(A1)(A1)(A1)
Notes: Award (A1) for correct window (at least one value, other than zero, labelled on each axis), the axes must also be labelled; (A1) for a smooth curve with the correct shape (graph should not touch \(y\)-axis and should not curve away from the \(y\)-axis), on the given domain; (A1) for axis intercept in approximately the correct position (nearer \(-5\) than zero); (A1) for local minimum in approximately the correct position (first quadrant, nearer the \(y\)-axis than \(x = 10\)).
If there is no scale, award a maximum of (A0)(A1)(A0)(A1) – the final (A1) being awarded for the zero and local minimum in approximately correct positions relative to each other.
\(( – 3.17,{\text{ }}0)\;\;\;\left( {( – 3.17480 \ldots ,{\text{ 0)}}} \right)\) (G1)(G1)
Notes: If parentheses are omitted award (G0)(G1)(ft).
Accept \(x = – 3.17,{\text{ }}y = 0\). Award (G1) for \(-3.17\) seen.
\(0 < x \leqslant 4{\text{ or }}0 < x < 4\) (A1)(A1)
Notes: Award (A1) for correct end points of interval, (A1) for correct notation (note: lower inequality must be strict).
Award a maximum of (A1)(A0) if \(y\) or \(f(x)\) used in place of \(x\).
Question
A cup of boiling water is placed in a room to cool. The temperature of the room is 20°C . This situation can be modelled by the exponential function \(T = a + b({k^{ – m}})\), where \(T\) is the temperature of the water, in °C , and \(m\) is the number of minutes for which the cup has been placed in the room. A sketch of the situation is given as follows.
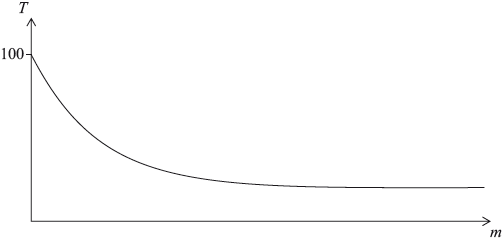
Explain why \(a = 20\).[2]
Initially, at \(m = 0\), the temperature of the water is 100°C.
Find the value of \(b\).[2]
After being placed in the room for one minute, the temperature of the water is 84°C.
Show that \(k = 1.25\).[2]
After being placed in the room for one minute, the temperature of the water is 84°C.
Find the temperature of the water three minutes after it has been placed in the room.[2]
After being placed in the room for one minute, the temperature of the water is 84°C.
Find the total time needed for the water to reach a temperature of 35°C. Give your answer in minutes and seconds, correct to the nearest second.[2]
Answer/Explanation
Markscheme
the temperature of the water cannot fall below room temperature (R1)
an (informal) explanation that as \(m \to \infty ,{\text{ }}{k^{ – m}} \to 0\) R1)
OR
recognition that there is a horizontal asymptote at \(y = a\) (R1)
Note: Award (R1) for a contextual reason involving room temperature.
Award (R1) for a mathematical reason similar to one of the two alternatives.
\(100 = 20 + b({k^0})\) (M1)
Note: Award (M1) for substituting \(100\), \(20\) and \(0\).
\(b = 80\) (A1)(G2)
Note: The (A1) is awarded only if all working seen is consistent with the final answer of \(80\).
\(84 = 20 + 80{k^{ – 1}}\) (M1)
Note: Substituting \(k = 1.25\) at any stage is an invalid method and is awarded (M0)(M0). Award (M1) for correctly substituting \(84\), \(20\) and their \(80\).
\(\frac{{64}}{{80}} = {k^{ – 1}}\) (M1)
\(k = 1.25\) (AG)
Note: Award (M1) for correct rearrangement that isolates \(k\); \(k = 1.25\) must be consistent with their working and the conclusion \(k = 1.25\) must be seen.
\(T = 20 + 80({1.25^{ – 3}})\) (M1)
Note: Award (M1) for their correct substitutions into \(T\). Follow through from part (b) and \(k = 1.25\).
\(T = 61.0\;\;\;(60.96)\) (A1)(ft)(G2)
\(35 = 20 + 80({1.25^{ – m}})\) (M1)
Note: Award (M1) for their correct substitutions into \(T\). Follow through from part (b). Accept graphical solutions. Award (M1) for sketch of function.
\((m = ){\text{ }}7.50{\text{ (minutes)}}\;\;\;{\text{(7.50179}} \ldots {\text{)}}\) (A1)(ft)(G2)
7 minutes and 30 seconds (A1)
Note: Award the final (A1) for correct conversion of their \(m\) in minutes to minutes and seconds, but only if answer in minutes is explicitly shown.
Question
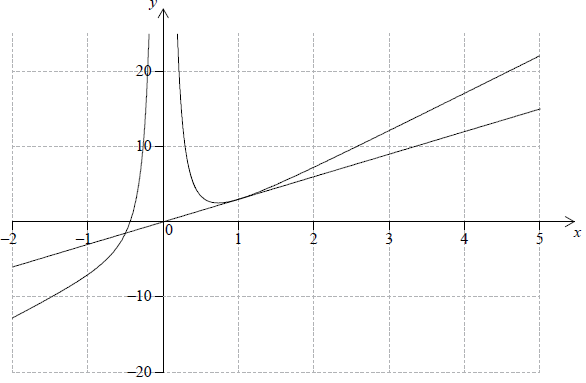
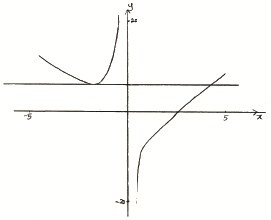
Consider the function \(f(x) = 0.5{x^2} – \frac{8}{x},{\text{ }}x \ne 0\).
Find \(f( – 2)\).[2]
Find \(f'(x)\).[3]
Find the gradient of the graph of \(f\) at \(x = – 2\).[2]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
Write down the equation of \(T\).[2]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
Sketch the graph of \(f\) for \( – 5 \leqslant x \leqslant 5\) and \( – 20 \leqslant y \leqslant 20\).[4]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
Draw \(T\) on your sketch.[2]
The tangent, \(T\), intersects the graph of \(f\) at a second point, P.
Use your graphic display calculator to find the coordinates of P.[2]
Answer/Explanation
Markscheme
\(0.5 \times {( – 2)^2} – \frac{8}{{ – 2}}\) (M1)
Note: Award (M1) for substitution of \(x = – 2\) into the formula of the function.
\(6\) (A1)(G2)
\(f'(x) = x + 8{x^{ – 2}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(x\), (A1) for \(8\), (A1) for \({x^{ – 2}}\) or \(\frac{1}{{{x^2}}}\) (each term must have correct sign). Award at most (A1)(A1)(A0) if there are additional terms present or further incorrect simplifications are seen.
\(f'( – 2) = – 2 + 8{( – 2)^{ – 2}}\) (M1)
Note: Award (M1) for \(x = – 2\) substituted into their \(f'(x)\) from part (b).
\( = 0\) (A1)(ft)(G2)
Note: Follow through from their derivative function.
\(y = 6\;\;\;\)OR\(\;\;\;y = 0x + 6\;\;\;\)OR\(\;\;\;y – 6 = 0(x + 2)\) (A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for their gradient from part (c), (A1)(ft) for their answer from part (a). Answer must be an equation.
Award (A0)(A0) for \(x = 6\).
(A1)(A1)(A1)(A1)
Notes: Award (A1) for labels and some indication of scales in the stated window. The point \((-2,{\text{ }}6)\) correctly labelled, or an \(x\)-value and a \(y\)-value on their axes in approximately the correct position, are acceptable indication of scales.
Award (A1) for correct general shape (curve must be smooth and must not cross the \(y\)-axis).
Award (A1) for \(x\)-intercept in approximately the correct position.
Award (A1) for local minimum in the second quadrant.
Tangent to graph drawn approximately at \(x = – 2\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for straight line tangent to curve at approximately \(x = – 2\), with approximately correct gradient. Tangent must be straight for the (A1)(ft) to be awarded.
Award (A1)(ft) for (extended) line passing through approximately their \(y\)-intercept from (d). Follow through from their gradient in part (c) and their equation in part (d).
\((4,{\text{ }}6)\;\;\;\)OR\(\;\;\;x = 4,{\text{ }}y = 6\) (G1)(ft)(G1)(ft)
Notes: Follow through from their tangent from part (d). If brackets are missing then award (G0)(G1)(ft).
If line intersects their graph at more than one point (apart from \(( – 2,{\text{ }}6)\)), follow through from the first point of intersection (to the right of \( – 2\)).
Award (G0)(G0) for \(( – 2,{\text{ }}6)\).
Question
A distress flare is fired into the air from a ship at sea. The height, \(h\) , in metres, of the flare above sea level is modelled by the quadratic function
\[h\,(t) = – 0.2{t^2} + 16t + 12\,,\,t \geqslant 0\,,\]
where \(t\) is the time, in seconds, and \(t = 0\,\) at the moment the flare was fired.
Write down the height from which the flare was fired.[1]
Find the height of the flare \(15\) seconds after it was fired.[2]
The flare fell into the sea \(k\) seconds after it was fired.
Find the value of \(k\) .[2]
Find \(h’\,(t)\,.\)[2]
i) Show that the flare reached its maximum height \(40\) seconds after being fired.
ii) Calculate the maximum height reached by the flare.[3]
The nearest coastguard can see the flare when its height is more than \(40\) metres above sea level.
Determine the total length of time the flare can be seen by the coastguard.[3]
Answer/Explanation
Markscheme
\(12\,({\text{m}})\) (A1)
\((h\,(15) = ) – 0.2 \times {15^2} + 16 \times 15 + 12\) (M1)
Note: Award (M1) for substitution of \(15\) in expression for \(h\).
\( = 207\,({\text{m}})\) (A1)(G2)
\(h\,(k) = 0\) (M1)
Note: Award (M1) for setting \(h\) to zero.
\((k = )\,\,\,80.7\,({\text{s}})\,\,\,(80.7430)\) (A1)(G2)
Note: Award at most (M1)(A0) for an answer including \(K = – 0.743\) .
Award (A0) for an answer of \(80\) without working.
\(h’\,(t) = – 0.4t + 16\) (A1)(A1)
Note: Award (A1) for \( – 0.4t\), (A1) for \(16\). Award at most (A1)(A0) if extra terms seen. Do not accept \(x\) for \(t\).
i) \( – 0.4t + 16 = 0\) (M1)
Note: Award (M1) for setting their derivative, from part (d), to zero, provided the correct conclusion is stated and consistent with their \(h’\,(t)\).
OR
\(t = \frac{{ – 16}}{{2 \times ( – 0.2)}}\) (M1)
Note: Award (M1) for correct substitution into axis of symmetry formula, provided the correct conclusion is stated.
\(t = \,\,40\,({\text{s}})\) (AG)
ii) \( – 0.2 \times {40^2} + 16 \times 40 + 12\) (M1)
Note: Award (M1) for substitution of \(40\) in expression for \(h\).
\( = 332\,({\text{m}})\) (A1)(G2)
\(h\,(t) = 40\) (M1)
Note: Award (M1) for setting \(h\) to \(40\). Accept inequality sign.
OR
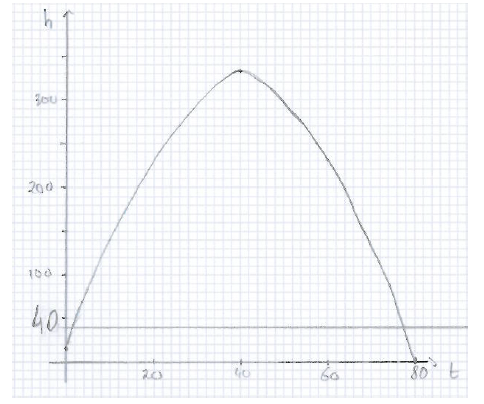
M1
Note: Award (M1) for correct sketch. Indication of scale is not required.
\(78.2 – 1.17\,\,(78.2099…\,\, – 1.79005…)\) (A1)
Note: Award (A1) for \(1.79\) and \(78.2\) seen.
(total time \( = \)) \(76.4\,({\text{s}})\,\,\,(76.4198…)\) (A1)(G2)
Note: Award (G1) if the two endpoints are given as the final answer with no working.
Question
A function, \(f\) , is given by
\[f(x) = 4 \times {2^{ – x}} + 1.5x – 5.\]
Calculate \(f(0)\)[2]
Use your graphic display calculator to solve \(f(x) = 0.\)[2]
Sketch the graph of \(y = f(x)\) for \( – 2 \leqslant x \leqslant 6\) and \( – 4 \leqslant y \leqslant 10\) , showing the \(x\) and \(y\) intercepts. Use a scale of \(2\,{\text{cm}}\) to represent \(2\) units on both the horizontal axis, \(x\) , and the vertical axis, \(y\) .[4]
The function \(f\) is the derivative of a function \(g\) . It is known that \(g(1) = 3.\)
i) Calculate \(g'(1).\)
ii) Find the equation of the tangent to the graph of \(y = g(x)\) at \(x = 1.\) Give your answer in the form \(y = mx + c.\)[4]
Answer/Explanation
Markscheme
\(4 \times {2^{ – 0}} + 1.5 \times 0 – 5\) (M1)
Note: Award (M1) for substitution of \(0\) into the expression for \(f(x)\) .
\( = – 1\) (A1)(G2)
\( – 0.538\,\,\,( – 0.537670…)\) and \(3\) (A1)(A1)
Note: Award at most (A0)(A1)(ft) if answer is given as pairs of coordinates.
(A1)(A1)(A1)(ft)(A1)(ft)
Note: Award (A1) for labels and some indication of scale in the correct given window.
Award (A1) for smooth curve with correct general shape with \(f( – 2) > f(6)\) and minimum to the right of the \(y\)-axis.
Award (A1)(ft) for correct \(y\)-intercept (consistent with their part (a)).
Award (A1)(ft) for approximately correct \(x\)-intercepts (consistent with their part (b), one zero between \( – 1\) and \(0\), the other between \(2.5\) and \(3.5\)).
i) \(g'(1) = f(1) = 4 \times {2^{ – 1}} + 1.5 – 5\) (M1)
Note: Award (M1) for substitution of \(1\) into \(f(x)\).
\( = – 1.5\) (A1)(G2)
ii) \(3 = – 1.5 \times 1 + c\) OR \((y – 3) = – 1.5\,(x – 1)\) (M1)
Note: Award (M1) for correct substitution of gradient and the point \((1,\,\,3)\) into the equation of a line. Follow through from (d)(i).
\(y = – 1.5x + 4.5\) (A1)(ft)(G2)
Question
The line \({L_1}\) has equation \(2y – x – 7 = 0\) and is shown on the diagram.
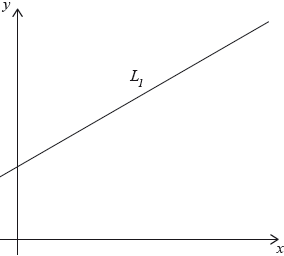
The point A has coordinates \((1,{\text{ }}4)\).
The point C has coordinates \((5,{\text{ }}12)\). M is the midpoint of AC.
The straight line, \({L_2}\), is perpendicular to AC and passes through M.
The point D is the intersection of \({L_1}\) and \({L_2}\).
The length of MD is \(\frac{{\sqrt {45} }}{2}\).
The point B is such that ABCD is a rhombus.
Show that A lies on \({L_1}\).[2]
Find the coordinates of M.[2]
Find the length of AC.[2]
Show that the equation of \({L_2}\) is \(2y + x – 19 = 0\).[5]
Find the coordinates of D.[2]
Write down the length of MD correct to five significant figures.[1]
Find the area of ABCD.[3]
Answer/Explanation
Markscheme
\(2 \times 4 – 1 – 7 = 0\) (or equivalent) (R1)
Note: For (R1) accept substitution of \(x = 1\) or \(y = 4\) into the equation followed by a confirmation that \(y = 4\) or \(x = 1\).
(since the point satisfies the equation of the line,) A lies on \({L_1}\) (A1)
Note: Do not award (A1)(R0).[2 marks]
\(\frac{{1 + 5}}{2}\) OR \(\frac{{4 + 12}}{2}\) seen (M1)
Note: Award (M1) for at least one correct substitution into the midpoint formula.
\((3,{\text{ }}8)\) (A1)(G2)
Notes: Accept \(x = 3,{\text{ }}y = 8\).
Award (M1)(A0) for \(\left( {\frac{{1 + 5}}{2},{\text{ }}\frac{{4 + 12}}{2}} \right)\).
Award (G1) for each correct coordinate seen without working.[2 marks]
\(\sqrt {{{(5 – 1)}^2} + {{(12 – 4)}^2}} \) (M1)
Note: Award (M1) for a correct substitution into distance between two points formula.
\( = 8.94{\text{ }}\left( {4\sqrt 5 ,{\text{ }}\sqrt {80} ,{\text{ }}8.94427 \ldots } \right)\) (A1)(G2)[2 marks]
gradient of \({\text{AC}} = \frac{{12 – 4}}{{5 – 1}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = 2\) (A1)
Note: Award (M1)(A1) for gradient of \({\text{AC}} = 2\) with or without working
gradient of the normal \( = – \frac{1}{2}\) (M1)
Note: Award (M1) for the negative reciprocal of their gradient of AC.
\(y – 8 = – \frac{1}{2}(x – 3)\) OR \(8 = – \frac{1}{2}(3) + c\) (M1)
Note: Award (M1) for substitution of their point and gradient into straight line formula. This (M1) can only be awarded where \( – \frac{1}{2}\) (gradient) is correctly determined as the gradient of the normal to AC.
\(2y – 16 = – (x – 3)\) OR \( – 2y + 16 = x – 3\) OR \(2y = – x + 19\) (A1)
Note: Award (A1) for correctly removing fractions, but only if their equation is equivalent to the given equation.
\(2y + x – 19 = 0\) (AG)
Note: The conclusion \(2y + x – 19 = 0\) must be seen for the (A1) to be awarded.
Where the candidate has shown the gradient of the normal to \({\text{AC}} = – 0.5\), award (M1) for \(2(8) + 3 – 19 = 0\) and (A1) for (therefore) \(2y + x – 19 = 0\).
Simply substituting \((3,{\text{ }}8)\) into the equation of \({L_2}\) with no other prior working, earns no marks.[5 marks]
\((6,{\text{ }}6.5)\) (A1)(A1)(G2)
Note: Award (A1) for 6, (A1) for 6.5. Award a maximum of (A1)(A0) if answers are not given as a coordinate pair. Accept \(x = 6,{\text{ }}y = 6.5\).
Award (M1)(A0) for an attempt to solve the two simultaneous equations \(2y – x – 7 = 0\) and \(2y + x – 19 = 0\) algebraically, leading to at least one incorrect or missing coordinate.[2 marks]
3.3541 (A1)
Note: Answer must be to 5 significant figures.[1 mark]
\(2 \times \frac{1}{2} \times \sqrt {80} \times \frac{{\sqrt {45} }}{2}\) (M1)(M1)
Notes: Award (M1) for correct substitution into area of triangle formula.
If their triangle is a quarter of the rhombus then award (M1) for multiplying their triangle by 4.
If their triangle is a half of the rhombus then award (M1) for multiplying their triangle by 2.
OR
\(\frac{1}{2} \times \sqrt {80} \times \sqrt {45} \) (M1)(M1)
Notes: Award (M1) for doubling MD to get the diagonal BD, (M1) for correct substitution into the area of a rhombus formula.
Award (M1)(M1) for \(\sqrt {80} \times \) their (f).
\( = 30\) (A1)(ft)(G3)
Notes: Follow through from parts (c) and (f).
\(8.94 \times 3.3541 = 29.9856 \ldots \)[3 marks]
Question
A water container is made in the shape of a cylinder with internal height \(h\) cm and internal base radius \(r\) cm.
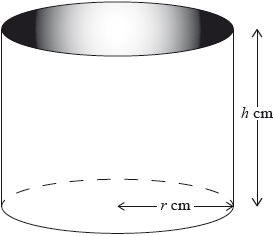
The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.
The volume of the water container is \(0.5{\text{ }}{{\text{m}}^3}\).
The water container is designed so that the area to be coated is minimized.
One can of water-resistant material coats a surface area of \(2000{\text{ c}}{{\text{m}}^2}\).
Write down a formula for \(A\), the surface area to be coated.[2]
Express this volume in \({\text{c}}{{\text{m}}^3}\).[1]
Write down, in terms of \(r\) and \(h\), an equation for the volume of this water container.[1]
Show that \(A = \pi {r^2}\frac{{1\,000\,000}}{r}\).[2]
Show that \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\).[2]
Find \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\).[3]
Using your answer to part (e), find the value of \(r\) which minimizes \(A\).[3]
Find the value of this minimum area.[2]
Find the least number of cans of water-resistant material that will coat the area in part (g).[3]
Answer/Explanation
Markscheme
\((A = ){\text{ }}\pi {r^2} + 2\pi rh\) (A1)(A1)
Note: Award (A1) for either \(\pi {r^2}\) OR \(2\pi rh\) seen. Award (A1) for two correct terms added together.[2 marks]
\(500\,000\) (A1)
Notes: Units not required.[1 mark]
\(500\,000 = \pi {r^2}h\) (A1)(ft)
Notes: Award (A1)(ft) for \(\pi {r^2}h\) equating to their part (b).
Do not accept unless \(V = \pi {r^2}h\) is explicitly defined as their part (b).[1 mark]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).[2 marks]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).[2 marks]
\(2\pi r – \frac{{{\text{1}}\,{\text{000}}\,{\text{000}}}}{{{r^2}}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi r\), (A1) for \(\frac{1}{{{r^2}}}\) or \({r^{ – 2}}\), (A1) for \( – {\text{1}}\,{\text{000}}\,{\text{000}}\).[3 marks]
\(2\pi r – \frac{{1\,000\,000}}{{{r^2}}} = 0\) (M1)
Note: Award (M1) for equating their part (e) to zero.
\({r^3} = \frac{{1\,000\,000}}{{2\pi }}\) OR \(r = \sqrt[3]{{\frac{{1\,000\,000}}{{2\pi }}}}\) (M1)
Note: Award (M1) for isolating \(r\).
OR
sketch of derivative function (M1)
with its zero indicated (M1)
\((r = ){\text{ }}54.2{\text{ }}({\text{cm}}){\text{ }}(54.1926 \ldots )\) (A1)(ft)(G2)[3 marks]
\(\pi {(54.1926 \ldots )^2} + \frac{{1\,000\,000}}{{(54.1926 \ldots )}}\) (M1)
Note: Award (M1) for correct substitution of their part (f) into the given equation.
\( = 27\,700{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}(27\,679.0 \ldots )\) (A1)(ft)(G2)[2 marks]
\(\frac{{27\,679.0 \ldots }}{{2000}}\) (M1)
Note: Award (M1) for dividing their part (g) by 2000.
\( = 13.8395 \ldots \) (A1)(ft)
Notes: Follow through from part (g).
14 (cans) (A1)(ft)(G3)
Notes: Final (A1) awarded for rounding up their \(13.8395 \ldots \) to the next integer.[3 marks]
Question
Violeta plans to grow flowers in a rectangular plot. She places a fence to mark out the perimeter of the plot and uses 200 metres of fence. The length of the plot is \(x\) metres.
Violeta places the fence so that the area of the plot is maximized.
By selling her flowers, Violeta earns 2 Bulgarian Levs (BGN) per square metre of the plot.
Violeta wants to invest her 5000 BGN.
A bank offers a nominal annual interest rate of 4%, compounded half-yearly.
Another bank offers an interest rate of \(r\)% compounded annually, that would allow her to double her money in 12 years.
Show that the width of the plot, in metres, is given by \(100 – x\).[1]
Write down the area of the plot in terms of \(x\).[1]
Find the value of \(x\) that maximizes the area of the plot.[2]
Show that Violeta earns 5000 BGN from selling the flowers grown on the plot.[2]
Find the amount of money that Violeta would have after 6 years. Give your answer correct to two decimal places.[3]
Find how long it would take for the interest earned to be 2000 BGN.[3]
Find the lowest possible value for \(r\).[2]
Answer/Explanation
Markscheme
\(\frac{{200 – 2x}}{2}\) (or equivalent) (M1)
OR
\(2x + 2y = 200\) (or equivalent) (M1)
Note: Award (M1) for a correct expression leading to \(100 – x\) (the \(100 – x\) does not need to be seen). The 200 must be seen for the (M1) to be awarded. Do not accept \(100 – x\) substituted in the perimeter of the rectangle formula.
\(100 – x\) (AG)[1 mark]
\(({\text{area}} = ){\text{ }}x(100 – x)\)\(\,\,\,\)OR\(\,\,\,\)\( – {x^2} + 100x\) (or equivalent) (A1)[1 mark]
\(x = \frac{{ – 100}}{{ – 2}}\)\(\,\,\,\)OR\(\,\,\,\)\( – 2x + 100 = 0\)\(\,\,\,\)OR\(\,\,\,\)graphical method (M1)
Note: Award (M1) for use of axis of symmetry formula or first derivative equated to zero or a sketch graph.
\(x = 50\) (A1)(ft)(G2)
Note: Follow through from part (b), provided x is positive and less than 100.[2 marks]
\(50(100 – 50) \times 2\) (M1)(M1)
Note: Award (M1) for substituting their \(x\) into their formula for area (accept “\(50 \times 50\)” for the substituted formula), and (M1) for multiplying by 2. Award at most (M0)(M1) if their calculation does not lead to 5000 (BGN), although the 5000 (BGN) does not need to be seen explicitly.
Substitution of 50 into area formula may be seen in part (c).
5000 (BGN) (AG)[2 marks]
\(5000{\left( {1 + \frac{4}{{2 \times 100}}} \right)^{2 \times 6}}\) (M1)(A1)
Note: Award (M1) for substitution into compound interest formula, (A1) for correct substitution.
OR
\({\text{N}} = 6\)
\({\text{I}}\% = 4\)
\({\text{PV}} = – 5000\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for \({\text{C/Y}} = 2\) seen, (M1) for other correct entries.
OR
\({\text{N}} = 12\)
\({\text{I}}\% = 4\)
\({\text{PV}} = – 5000\)
\({\text{P/Y}} = 2\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for \({\text{C/Y}} = 2\) seen, (M1) for other correct entries.
6341.21 (BGN) (A1)(G3)
Note: Award (A1) for correct answer, to two decimal places only.
Award (G2) for 6341.20 or a correct, unrounded final answer if no working is seen (6341.2089…).[3 marks]
\(5000{\left( {1 + \frac{4}{{2 \times 100}}} \right)^{2 \times t}} = 7000\) (M1)(A1)(ft)
Note: Award (M1) for using the compound interest formula with a variable for time, (A1)(ft) for substituting the correct values and equating to 7000. Follow through for their “2” from part (e)(i).
OR
\({\text{I% }} = 4\)
\({\text{PV}} = ( \pm )5000\)
\({\text{FV}} = \mp 7000\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for 7000 seen, (M1) for the other correct entries.
Award (M1) for their C/Y from part (e)(i).
OR
\({\text{I% }} = 4\)
\({\text{PV}} = ( \pm )5000\)
\({\text{FV}} = \mp 7000\)
\({\text{P/Y}} = 2\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for 7000 seen, (M1) for the other correct entries.
Award (M1) for their C/Y from part (e)(i).
OR
(M1)(A1)(ft)
Note: Award (M1) for a sketch with a straight line intercepted by appropriate curve, (A1)(ft) for numerical answer in the range of 8.4 and 8.5.
Follow through from their part (e)(i).
\(t = 8.50{\text{ (years) }}(8.49564 \ldots )\) (A1)(ft)(G3)
Note: Award only (A1) if 16.9912… is seen without working. If working is seen, award at most (M1)(A1)(A0).[3 marks]
\(5000{\left( {1 + \frac{r}{{100}}} \right)^{12}} = 10000\) (M1)
Note: Award (M1) for correct substitution into compound interest formula with 10 000 seen.
OR
\(2 = {\left( {1 + \frac{r}{{100}}} \right)^{12}}\) (M1)
Note: Award (M1) for correct substitution and simplification of compound interest formula, equating to 2.
\(r = 5.95{\text{ (% ) }}(5.94630 \ldots )\) (A1)(G2)[2 marks]
Question
Consider the function \(f(x) = – {x^4} + a{x^2} + 5\), where \(a\) is a constant. Part of the graph of \(y = f(x)\) is shown below.
It is known that at the point where \(x = 2\) the tangent to the graph of \(y = f(x)\) is horizontal.
There are two other points on the graph of \(y = f(x)\) at which the tangent is horizontal.
Write down the \(y\)-intercept of the graph.[1]
Find \(f'(x)\).[2]
Show that \(a = 8\).[2]
Find \(f(2)\).[2]
Write down the \(x\)-coordinates of these two points;[2]
Write down the intervals where the gradient of the graph of \(y = f(x)\) is positive.[2]
Write down the range of \(f(x)\).[2]
Write down the number of possible solutions to the equation \(f(x) = 5\).[1]
The equation \(f(x) = m\), where \(m \in \mathbb{R}\), has four solutions. Find the possible values of \(m\).[2]
Answer/Explanation
Markscheme
5 (A1)
Note: Accept an answer of \((0,{\text{ }}5)\).[1 mark]
\(\left( {f'(x) = } \right) – 4{x^3} + 2ax\) (A1)(A1)
Note: Award (A1) for \( – 4{x^3}\) and (A1) for \( + 2ax\). Award at most (A1)(A0) if extra terms are seen.[2 marks]
\( – 4 \times {2^3} + 2a \times 2 = 0\) (M1)(M1)
Note: Award (M1) for substitution of \(x = 2\) into their derivative, (M1) for equating their derivative, written in terms of \(a\), to 0 leading to a correct answer (note, the 8 does not need to be seen).
\(a = 8\) (AG)[2 marks]
\(\left( {f(2) = } \right) – {2^4} + 8 \times {2^2} + 5\) (M1)
Note: Award (M1) for correct substitution of \(x = 2\) and \(a = 8\) into the formula of the function.
21 (A1)(G2)[2 marks]
\((x = ){\text{ }} – 2,{\text{ }}(x = ){\text{ 0}}\) (A1)(A1)
Note: Award (A1) for each correct solution. Award at most (A0)(A1)(ft) if answers are given as \(( – 2{\text{ }},21)\) and \((0,{\text{ }}5)\) or \(( – 2,{\text{ }}0)\) and \((0,{\text{ }}0)\).[2 marks]
\(x < – 2,{\text{ }}0 < x < 2\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for \(x < – 2\), follow through from part (d)(i) provided their value is negative.
Award (A1)(ft) for \(0 < x < 2\), follow through only from their 0 from part (d)(i); 2 must be the upper limit.
Accept interval notation.[2 marks]
\(y \leqslant 21\) (A1)(ft)(A1)
Notes: Award (A1)(ft) for 21 seen in an interval or an inequality, (A1) for “\(y \leqslant \)”.
Accept interval notation.
Accept \( – \infty < y \leqslant 21\) or \(f(x) \leqslant 21\).
Follow through from their answer to part (c)(ii). Award at most (A1)(ft)(A0) if \(x\) is seen instead of \(y\). Do not award the second (A1) if a (finite) lower limit is seen.[2 marks]
3 (solutions) (A1)[1 mark]
\(5 < m < 21\) or equivalent (A1)(ft)(A1)
Note: Award (A1)(ft) for 5 and 21 seen in an interval or an inequality, (A1) for correct strict inequalities. Follow through from their answers to parts (a) and (c)(ii).
Accept interval notation.[2 marks]
Question
A deep sea diver notices that the intensity of light, \(I\) , below the surface of the ocean decreases with depth, \(d\) , according to the formula
\[I = k{(1.05)^{ – d}}{\text{,}}\]where \(I\) is expressed as a percentage, \(d\) is the depth in metres below the surface and \(k\) is a constant.
The intensity of light at the surface is \(100\% \).
Calculate the value of \(k\) .[2]
Find the intensity of light at a depth \(25{\text{ m}}\) below the surface.[2]
To be able to see clearly, a diver needs the intensity of light to be at least \(65\% \).
Using your graphic display calculator, find the greatest depth below the surface at which she can see clearly.[2]
The table below gives the intensity of light (correct to the nearest integer) at different depths.
Using this information draw the graph of \(I\) against \(d\) for \(0 \leqslant d \leqslant 100\) . Use a scale of \(1{\text{ cm}}\) to represent 10 metres on the horizontal axis and 1 cm to represent \(10\% \) on the vertical axis.[4]
Some sea creatures have adapted so they can see in low intensity light and cannot tolerate too much light.
Indicate clearly on your graph the range of depths sea creatures could inhabit if they can tolerate between \(5\% \) and \(35\% \) of the light intensity at the surface.[2]
Answer/Explanation
Markscheme
\(d = 0\), \(k = 100\) (M1)(A1)(G2)
Note: Award (M1) for \(d = 0\) seen.
\(I = 100 \times {(1.05)^{ – 25}} = 29.5(\% )\) (\(29.5302 \ldots \)) (M1)(A1)(ft)(G2)
\(65 = 100 \times {(1.05)^{ – d}}\) (M1)
Note: Award (M1) for sketch with line drawn at \(y = 65\) .
\(d = 8.83{\text{ (m)}}\) (\(8.82929 \ldots \)) (A1)(ft)(G2)
(A1) for labels and scales
(A2) for all points correct, (A1) for 3 or 4 points correct
(A1) for smooth curve asymptotic to the \(x\)-axis (A4)
Lines in approx correct positions on graph (M1)
The range of values indicated (arrows or shading) \(22\)–\(60{\text{ m}}\) (A1)