Download IITian Academy App for accessing Online Mock Tests and More..
Question
The figure below shows the graphs of functions \(f_1 (x) = x\) and \(f_2 (x) = 5 – x^2\).
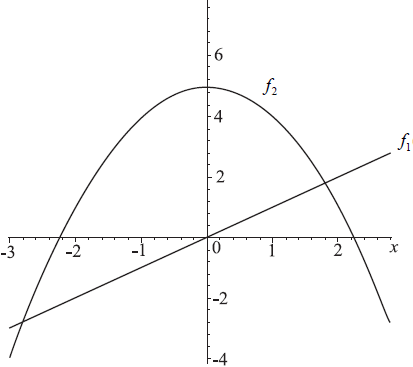
(i) Differentiate \(f_1 (x) \) with respect to x.
(ii) Differentiate \(f_2 (x) \) with respect to x.[3]
Calculate the value of x for which the gradient of the two graphs is the same.[2]
Draw the tangent to the curved graph for this value of x on the figure, showing clearly the property in part (b).[1]
Answer/Explanation
Markscheme
(i) \(f_1 ‘ (x) = 1\) (A1)
(ii) \(f_2 ‘ (x) = – 2x\) (A1)(A1)
(A1) for correct differentiation of each term. (C3)[3 marks]
\(1 = – 2x\) (M1)
\(x = – \frac{1}{2}\) (A1)(ft) (C2)[2 marks]
(A1) is for the tangent drawn at \(x = \frac{1}{2}\) and reasonably parallel to the line \(f_1\) as shown.
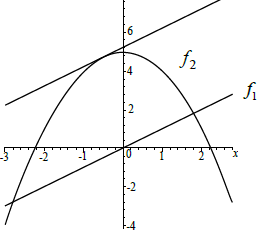(A1) (C1)[1 mark]
Question
The table given below describes the behaviour of f ′(x), the derivative function of f (x), in the domain −4 < x < 2.
State whether f (0) is greater than, less than or equal to f (−2). Give a reason for your answer.[2]
The point P(−2, 3) lies on the graph of f (x).
Write down the equation of the tangent to the graph of f (x) at the point P.[2]
The point P(−2, 3) lies on the graph of f (x).
From the information given about f ′(x), state whether the point (−2, 3) is a maximum, a minimum or neither. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
greater than (A1)
Gradient between x = −2 and x = 0 is positive. (R1)
OR
The function is increased between these points or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
y = 3 (A1)(A1) (C2)
Note: Award (A1) for y = a constant, (A1) for 3.[2 marks]
minimum (A1)
Gradient is negative to the left and positive to the right or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
Question
Consider the curve \(y = {x^2} + \frac{a}{x} – 1,{\text{ }}x \ne 0\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[3]
The gradient of the tangent to the curve is \( – 14\) when \(x = 1\).
Find the value of \(a\).[3]
Answer/Explanation
Markscheme
\(2x – \frac{a}{{{x^2}}}\) (A1)(A1)(A1) (C3)
Notes: Award (A1) for \(2x\), (A1) for \( – a\) and (A1) for \({x^{ – 2}}\).
Award at most (A1)(A1)(A0) if extra terms are present.
\(2(1) – \frac{a}{{{1^2}}} = – 14\) (M1)(M1)
Note: Award (M1) for substituting \(1\) into their gradient function, (M1) for equating their gradient function to \( – 14\).
Award (M0)(M0)(A0) if the original function is used instead of the gradient function.
\(a = 16\) (A1)(ft) (C3)
Note: Follow through from their gradient function from part (a).
Question
A function \(f\) is given by \(f(x) = 4{x^3} + \frac{3}{{{x^2}}} – 3,{\text{ }}x \ne 0\).
Write down the derivative of \(f\).[3]
Find the point on the graph of \(f\) at which the gradient of the tangent is equal to 6.[3]
Answer/Explanation
Markscheme
\(12{x^2} – \frac{6}{{{x^3}}}\) or equivalent (A1)(A1)(A1) (C3)
Note: Award (A1) for \(12{x^2}\), (A1) for \( – 6\) and (A1) for \(\frac{1}{{{x^3}}}\) or \({x^{ – 3}}\). Award at most (A1)(A1)(A0) if additional terms seen.[3 marks]
\(12{x^2} – \frac{6}{{{x^3}}} = 6\) (M1)
Note: Award (M1) for equating their derivative to 6.
\((1,{\text{ }}4)\)\(\,\,\,\)OR\(\,\,\,\)\(x = 1,{\text{ }}y = 4\) (A1)(ft)(A1)(ft) (C3)
Note: A frequent wrong answer seen in scripts is \((1,{\text{ }}6)\) for this answer with correct working award (M1)(A0)(A1) and if there is no working award (C1).[3 marks]
Question
The point A has coordinates (4 , −8) and the point B has coordinates (−2 , 4).
The point D has coordinates (−3 , 1).
Write down the coordinates of C, the midpoint of line segment AB.[2]
Find the gradient of the line DC.[2]
Find the equation of the line DC. Write your answer in the form ax + by + d = 0 where a , b and d are integers.[2]
Answer/Explanation
Markscheme
(1, −2) (A1)(A1) (C2)
Note: Award (A1) for 1 and (A1) for −2, seen as a coordinate pair.
Accept x = 1, y = −2. Award (A1)(A0) if x and y coordinates are reversed.[2 marks]
\(\frac{{1 – \left( { – 2} \right)}}{{ – 3 – 1}}\) (M1)
Note: Award (M1) for correct substitution, of their part (a), into gradient formula.
\( = – \frac{3}{4}\,\,\,\left( { – 0.75} \right)\) (A1)(ft) (C2)
Note: Follow through from part (a).[2 marks]
\(y – 1 = – \frac{3}{4}\left( {x + 3} \right)\) OR \(y + 2 = – \frac{3}{4}\left( {x – 1} \right)\) OR \(y = – \frac{3}{4}x – \frac{5}{4}\) (M1)
Note: Award (M1) for correct substitution of their part (b) and a given point.
OR
\(1 = – \frac{3}{4} \times – 3 + c\) OR \( – 2 = – \frac{3}{4} \times 1 + c\) (M1)
Note: Award (M1) for correct substitution of their part (b) and a given point.
\(3x + 4y + 5 = 0\) (accept any integer multiple, including negative multiples) (A1)(ft) (C2)
Note: Follow through from parts (a) and (b). Where the gradient in part (b) is found to be \(\frac{5}{0}\), award at most (M1)(A0) for either \(x = – 3\) or \(x + 3 = 0\).[2 marks]
Question
Consider the function \(f\left( x \right) = \frac{{{x^4}}}{4}\).
Find f’(x)[1]
Find the gradient of the graph of f at \(x = – \frac{1}{2}\).[2]
Find the x-coordinate of the point at which the normal to the graph of f has gradient \({ – \frac{1}{8}}\).[3]
Answer/Explanation
Markscheme
x3 (A1) (C1)
Note: Award (A0) for \(\frac{{4{x^3}}}{4}\) and not simplified to x3.[1 mark]
\({\left( { – \frac{1}{2}} \right)^3}\) (M1)
Note: Award (M1) for correct substitution of \({ – \frac{1}{2}}\) into their derivative.
\({ – \frac{1}{8}}\) (−0.125) (A1)(ft) (C2)
Note: Follow through from their part (a).[2 marks]
x3 = 8 (A1)(M1)
Note: Award (A1) for 8 seen maybe seen as part of an equation y = 8x + c, (M1) for equating their derivative to 8.
(x =) 2 (A1) (C3)
Note: Do not accept (2, 4).[3 marks]
Question
Consider the graph of the function \(y = f(x)\) defined below.
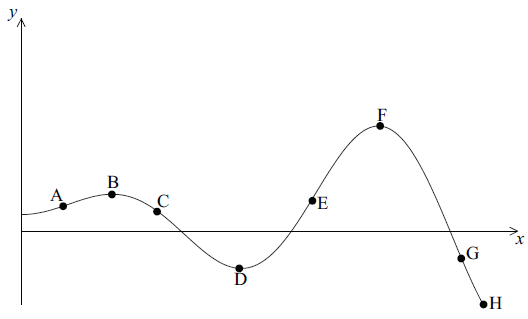
Write down all the labelled points on the curve
that are local maximum points;[1]
where the function attains its least value;[1]
where the function attains its greatest value;[1]
where the gradient of the tangent to the curve is positive;[1]
where \(f(x) > 0\) and \(f'(x) < 0\) .[2]
Answer/Explanation
Markscheme
B, F (C1)
H (C1)
F (C1)
A, E (C1)
C (C2)
Question
Consider the curve \(y = {x^2}\) .
Write down \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[1]
The point \({\text{P}}(3{\text{, }}9)\) lies on the curve \(y = {x^2}\) . Find the gradient of the tangent to the curve at P .[2]
The point \({\text{P}}(3{\text{, }}9)\) lies on the curve \(y = {x^2}\) . Find the equation of the normal to the curve at P . Give your answer in the form \(y = mx + c\) .[3]
Answer/Explanation
Markscheme
\(2x\) (A1) (C1)
\(2 \times 3\) (M1)
\( = 6\) (A1) (C2)
\(m({\text{perp}}) = – \frac{1}{6}\) (A1)(ft)
Note: Follow through from their answer to part (b).
Equation \((y – 9) = – \frac{1}{6}(x – 3)\) (M1)
Note: Award (M1) for correct substitution in any formula for equation of a line.
\(y = – \frac{1}{6}x + 9\frac{1}{2}\) (A1)(ft) (C3)
Note: Follow through from correct substitution of their gradient of the normal.
Note: There are no extra marks awarded for rearranging the equation to the form \(y = mx + c\) .