Question
The figure below shows the graphs of functions \(f_1 (x) = x\) and \(f_2 (x) = 5 – x^2\).
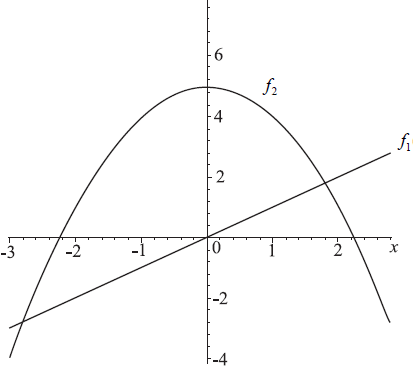
(i) Differentiate \(f_1 (x) \) with respect to x.
(ii) Differentiate \(f_2 (x) \) with respect to x.[3]
Calculate the value of x for which the gradient of the two graphs is the same.[2]
Draw the tangent to the curved graph for this value of x on the figure, showing clearly the property in part (b).[1]
Answer/Explanation
Markscheme
(i) \(f_1 ‘ (x) = 1\) (A1)
(ii) \(f_2 ‘ (x) = – 2x\) (A1)(A1)
(A1) for correct differentiation of each term. (C3)[3 marks]
\(1 = – 2x\) (M1)
\(x = – \frac{1}{2}\) (A1)(ft) (C2)[2 marks]
(A1) is for the tangent drawn at \(x = \frac{1}{2}\) and reasonably parallel to the line \(f_1\) as shown.
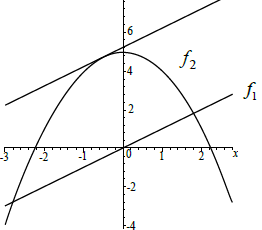(A1) (C1)[1 mark]
Question
Consider the function \(f(x) = 2{x^3} – 5{x^2} + 3x + 1\).
Find \(f'(x)\).[3]
Write down the value of \(f'(2)\).[1]
Find the equation of the tangent to the curve of \(y = f(x)\) at the point \((2{\text{, }}3)\).[2]
Answer/Explanation
Markscheme
\(f'(x) = 6{x^2} – 10x + 3\) (A1)(A1)(A1) (C3)
Notes: Award (A1) for each correct term and no extra terms.
Award (A1)(A1)(A0) if each term correct and extra term seen.
Award(A1)(A0)(A0) if two terms correct and extra term seen.
Award (A0) otherwise.[3 marks]
\(f'(2) = 7\) (A1)(ft) (C1)[1 mark]
\(y = 7x – 11\) or equivalent (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) on their (b) for \(7x\) (must have \(x\)), (A1)(ft) for \( – 11\). Accept \(y – 3 = 7(x – 2)\) .[2 marks]
Question
Consider the function \(f(x) = \frac{1}{2}{x^3} – 2{x^2} + 3\).
Find \(f'(x)\).[2]
Find \(f”(x)\).[2]
Find the equation of the tangent to the curve of \(f\) at the point \((1{\text{, }}1.5)\).[2]
Answer/Explanation
Markscheme
\(\frac{{3{x^2}}}{2} – 4x\) (A1)(A1) (C2)
Note: Award (A1) for each correct term and no extra terms; award (A1)(A0) for both terms correct and extra terms; (A0) otherwise.[2 marks]
\(3x – 4\) (A1)(ft)(A1)(ft) (C2)
Note: accept \(3{x^1} – {4^0}\)[2 marks]
\(y = – 2.5x + 4\) or equivalent (A1)(ft)(A1) (C2)
Note: Award (A1)(ft) on their (a) for \( – 2.5x\) (must have \(x\)), (A1) for \(4\) or equivalent correct answer only.
Accept \(y – 1.5 = – 2.5(x – 1)\)[2 marks]
Question
The function \(f(x)\) is such that \(f'(x) < 0\) for \(1 < x < 4\). At the point \({\text{P}}(4{\text{, }}2)\) on the graph of \(f(x)\) the gradient is zero.
Write down the equation of the tangent to the graph of \(f(x)\) at \({\text{P}}\).[2]
State whether \(f(4)\) is greater than, equal to or less than \(f(2)\).[2]
Given that \(f(x)\) is increasing for \(4 \leqslant x < 7\), what can you say about the point \({\text{P}}\)?[2]
Answer/Explanation
Markscheme
\(y = 2\). (A1)(A1) (C2)
Note: Award (A1) for \(y = \ldots \), (A1) for \(2\).
Accept \(f(x) = 2\) and \(y = 0x + 2\)
Less (than). (A2) (C2)[2 marks]
Local minimum (accept minimum, smallest or equivalent) (A2) (C2)
Note: Award (A1) for stationary or turning point mentioned.
No mark is awarded for \({\text{gradient}} = 0\) as this is given in the question.
Question
The straight line, L, has equation \(2y – 27x – 9 = 0\).
Find the gradient of L.[2]
Sarah wishes to draw the tangent to \(f (x) = x^4\) parallel to L.
Write down \(f ′(x)\).[1]
Find the x coordinate of the point at which the tangent must be drawn.[2]
Write down the value of \(f (x)\) at this point.[1]
Answer/Explanation
Markscheme
y = 13.5x + 4.5 (M1)
Note: Award (M1) for 13.5x seen.
gradient = 13.5 (A1) (C2)[2 marks]
4x3 (A1) (C1)[1 mark]
4x3 = 13.5 (M1)
Note: Award (M1) for equating their answers to (a) and (b).
x = 1.5 (A1)(ft)[2 marks]
\(\frac{{81}}{{16}}\) (5.0625, 5.06) (A1)(ft) (C3)
Note: Award (A1)(ft) for substitution of their (c)(i) into x4 with working seen.[1 mark]
Question
Consider \(f:x \mapsto {x^2} – 4\).
Find \(f ′(x)\).[1]
Let L be the line with equation y = 3x + 2.
Write down the gradient of a line parallel to L.[1]
Let L be the line with equation y = 3x + 2.
Let P be a point on the curve of f. At P, the tangent to the curve is parallel to L. Find the coordinates of P.[4]
Answer/Explanation
Markscheme
\(2x\) (A1) (C1)[1 mark]
3 (A1) (C1)[1 mark]
\(2x = 3\) (M1)
Note: (M1) for equating their (a) to their (b).
\(x =1.5\) (A1)(ft)
\(y = (1.5)^2 – 4\) (M1)
Note: (M1) for substituting their x in f (x).
(1.5, −1.75) (accept x = 1.5, y = −1.75) (A1)(ft) (C4)
Note: Missing coordinate brackets receive (A0) if this is the first time it occurs.[4 marks]
Question
Let \(f (x) = 2x^2 + x – 6\)
Find \(f'(x)\).[3]
Find the value of \(f'( – 3)\).[1]
Find the value of \(x\) for which \(f'(x) = 0\).[2]
Answer/Explanation
Markscheme
\(f'(x) = 4x + 1\) (A1)(A1)(A1) (C3)
Note: Award (A1) for each term differentiated correctly.
Award at most (A1)(A1)(A0) if any extra terms seen.[3 marks]
\(f'( – 3) = – 11\) (A1)(ft) (C1)[1 mark]
\(4x + 1 = 0\) (M1)
\(x = – \frac{{1}}{{4}}\) (A1)(ft) (C2)[2 marks]
Question
The table given below describes the behaviour of f ′(x), the derivative function of f (x), in the domain −4 < x < 2.
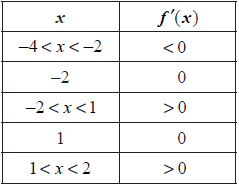
State whether f (0) is greater than, less than or equal to f (−2). Give a reason for your answer.[2]
The point P(−2, 3) lies on the graph of f (x).
Write down the equation of the tangent to the graph of f (x) at the point P.[2]
The point P(−2, 3) lies on the graph of f (x).
From the information given about f ′(x), state whether the point (−2, 3) is a maximum, a minimum or neither. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
greater than (A1)
Gradient between x = −2 and x = 0 is positive. (R1)
OR
The function is increased between these points or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
y = 3 (A1)(A1) (C2)
Note: Award (A1) for y = a constant, (A1) for 3.[2 marks]
minimum (A1)
Gradient is negative to the left and positive to the right or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
Question
The figure shows the graphs of the functions \(f(x) = \frac{1}{4}{x^2} – 2\) and \(g(x) = x\) .
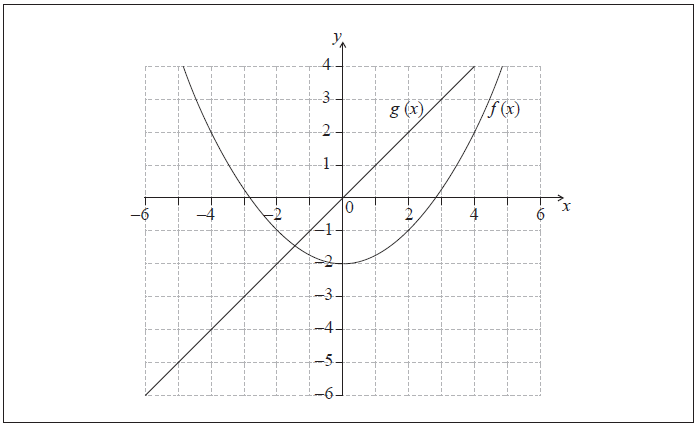
Differentiate \(f(x)\) with respect to \(x\) .[1]
Differentiate \(g(x)\) with respect to \(x\) .[1]
Calculate the value of \(x\) for which the gradients of the two graphs are the same.[2]
Draw the tangent to the parabola at the point with the value of \(x\) found in part (c).[2]
Answer/Explanation
Markscheme
\(\frac{1}{2}x{\text{ }}\left( {\frac{2}{4}x} \right)\) (A1) (C1)
Note: Accept an equivalent, unsimplified expression (i.e. \(2 \times \frac{1}{4}x\)).[1 mark]
\(1\) (A1) (C1)[1 mark]
\(\frac{1}{2}x = 1\) (M1)
\(x = 2\) (A1)(ft) (C2)
Notes: Award (M1)(A0) for coordinate pair \((2{\text{, }} – 1)\) seen with or without working. Follow through from their answers to parts (a) and (b).[2 marks]
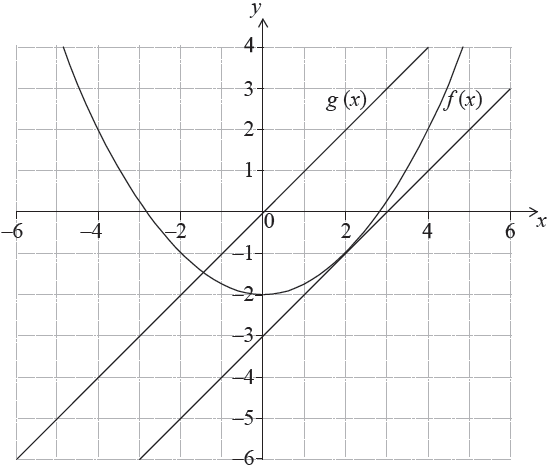
tangent drawn to the parabola at the \(x\)-coordinate found in part (c) (A1)(ft)
candidate’s attempted tangent drawn parallel to the graph of \(g(x)\) (A1)(ft) (C2)[2 marks]
Question
The equation of a curve is given as \(y = 2x^{2} – 5x + 4\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
The equation of the line L is \(6x + 2y = -1\).
Find the x-coordinate of the point on the curve \(y = 2x^2 – 5x + 4\) where the tangent is parallel to L.[4]
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 4x – 5\) (A1)(A1) (C2)
Notes: Award (A1) for each correct term. Award (A1)(A0) if any other terms are given.[2 marks]
\(y = – 3x – \frac{1}{2}\) (M1)
Note: Award (M1) for rearrangement of equation
gradient of line is –3 (A1)
\(4x – 5 = -3\) (M1)
Notes: Award (M1) for equating their gradient to their derivative from part (a). If \(4x – 5 = -3\) is seen with no working award (M1)(A1)(M1).
\(x = \frac{1}{2}\) (A1)(ft) (C4)
Note: Follow through from their part (a). If answer is given as (0.5, 2) with no working award the final (A1) only.[4 marks]
Question
A curve is described by the function \(f (x) = 3x – \frac{2}{{x^2}}\), \(x \ne 0\).
Find \(f ‘ (x) \).[3]
The gradient of the curve at point A is 35.
Find the x-coordinate of point A.[3]
Answer/Explanation
Markscheme
\(f'(x) = 3 + \frac{4}{{{x^3}}}\) (A1)(A1)(A1) (C3)
Notes: Award (A1) for 3, (A1) for + 4 and (A1) for \(\frac{1}{{{x^3}}}\) or \(x^{-3}\). Award at most (A1)(A1)(A0) if additional terms are seen.
\(3 + \frac{4}{{{x^3}}} = 35\) (M1)
Note: Award (M1) for equating their derivative to 35 only if the derivative is not a constant.
\({x^3} = \frac{1}{8}\) (A1)(ft)
\(\frac{1}{2}(0.5)\) (A1)(ft) (C3)
Question
Let \(f(x) = {x^4}\).
Write down \(f'(x)\).[1]
Point \({\text{P}}(2,6)\) lies on the graph of \(f\).
Find the gradient of the tangent to the graph of \(y = f(x)\) at \({\text{P}}\).[2]
Point \({\text{P}}(2,16)\) lies on the graph of \(f\).
Find the equation of the normal to the graph at \({\text{P}}\). Give your answer in the form \(ax + by + d = 0\), where \(a\), \(b\) and \(d\) are integers.[3]
Answer/Explanation
Markscheme
\(\left( {f'(x) = } \right)\) \(4{x^3}\) (A1) (C1)[1 mark]
\(4 \times {2^3}\) (M1)
Note: Award (M1) for substituting 2 into their derivative.
\( = 32\) (A1)(ft) (C2)
Note: Follow through from their part (a).[2 marks]
\(y – 16 = – \frac{1}{{32}}(x – 2)\) or \(y = – \frac{1}{{32}}x + \frac{{257}}{{16}}\) (M1)(M1)
Note: Award (M1) for their gradient of the normal seen, (M1) for point substituted into equation of a straight line in only \(x\) and \(y\) (with any constant ‘\(c\)’ eliminated).
\(x + 32y – 514 = 0\) or any integer multiple (A1)(ft) (C3)
Note: Follow through from their part (b).[3 marks]
Question
Consider the graph of the function \(f(x) = {x^3} + 2{x^2} – 5\).
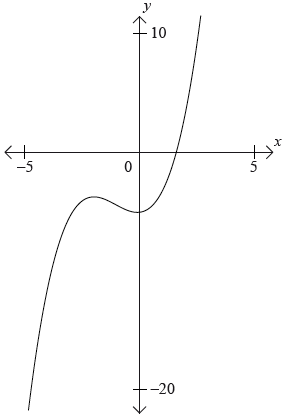
Label the local maximum as \({\text{A}}\) on the graph.[1]
Label the local minimum as B on the graph.[1]
Write down the interval where \(f'(x) < 0\).[1]
Draw the tangent to the curve at \(x = 1\) on the graph.[1]
Write down the equation of the tangent at \(x = 1\).[2]
Answer/Explanation
Markscheme
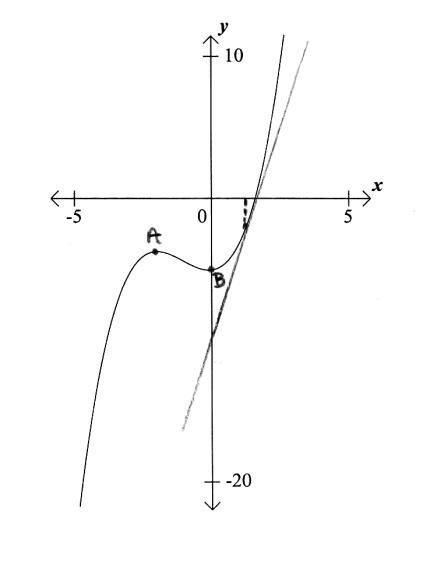
correct label on graph (A1) (C1)[1 mark]
correct label on graph (A1) (C1)[1 mark]
\( – 1.33 < x < 0\) \(\left( { – \frac{4}{3} < x < 0} \right)\) (A1) (C1)[1 mark]
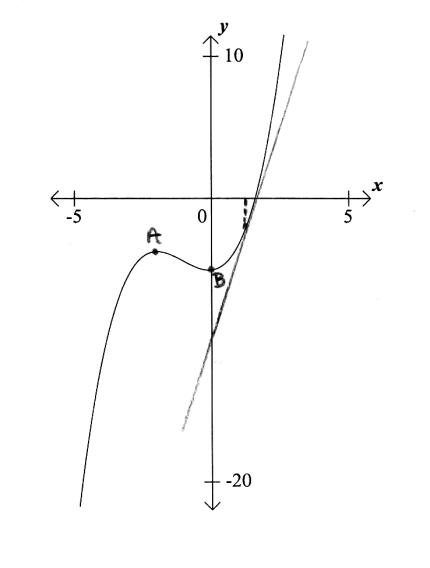
tangent drawn at \(x = 1\) on graph (A1) (C1)[1 mark]
\(y = 7x – 9\) (A1)(A1) (C2)
Notes: Award (A1) for \(7\), (A1) for \(-9\).
If answer not given as an equation award at most (A1)(A0).[2 marks]
Question
Consider the curve \(y = {x^2} + \frac{a}{x} – 1,{\text{ }}x \ne 0\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[3]
The gradient of the tangent to the curve is \( – 14\) when \(x = 1\).
Find the value of \(a\).[3]
Answer/Explanation
Markscheme
\(2x – \frac{a}{{{x^2}}}\) (A1)(A1)(A1) (C3)
Notes: Award (A1) for \(2x\), (A1) for \( – a\) and (A1) for \({x^{ – 2}}\).
Award at most (A1)(A1)(A0) if extra terms are present.
\(2(1) – \frac{a}{{{1^2}}} = – 14\) (M1)(M1)
Note: Award (M1) for substituting \(1\) into their gradient function, (M1) for equating their gradient function to \( – 14\).
Award (M0)(M0)(A0) if the original function is used instead of the gradient function.
\(a = 16\) (A1)(ft) (C3)
Note: Follow through from their gradient function from part (a).
Question
The equation of line \({L_1}\) is \(y = 2.5x + k\). Point \({\text{A}}\) \(\,(3,\, – 2)\) lies on \({L_1}\).
Find the value of \(k\).[2]
The line \({L_2}\) is perpendicular to \({L_1}\) and intersects \({L_1}\) at point \({\text{A}}\).
Write down the gradient of \({L_2}\).[1]
Find the equation of \({L_2}\). Give your answer in the form \(y = mx + c\) .[2]
Write your answer to part (c) in the form \(ax + by + d = 0\) where \(a\), \(b\) and \(d \in \mathbb{Z}\).[1]
Answer/Explanation
Markscheme
\( – 2 = 2.5\, \times 3 + k\) (M1)
Note: Award (M1) for correct substitution of \((3,\, – 2)\) into equation of \({L_1}\).
\((k = ) – 9.5\) (A1) (C2)
\( – 0.4\,\left( { – \frac{2}{5}} \right)\) (A1) (C1)
\(y – ( – 2) = – 0.4\,(x – 3)\) (M1)
OR
\( – 2 = – 0.4\,(3) + c\) (M1)
Note: Award (M1) for their gradient and given point substituted into equation of a straight line. Follow through from part (b).
\(y = – 0.4x – 0.8\) \(\left( {y = – \frac{2}{5}x – \frac{4}{5}} \right)\) (A1)(ft) (C2)
\(2x + 5y + 4 = 0\) (or any integer multiple) (A1)(ft) (C1)
Note: Follow through from part (c).
Question
Consider the function \(f(x) = a{x^2} + c\).
Find \(f'(x)\)[1]
Point \({\text{A}}( – 2,\,5)\) lies on the graph of \(y = f(x)\) . The gradient of the tangent to this graph at \({\text{A}}\) is \( – 6\) .
Find the value of \(a\) .[3]
Find the value of \(c\) .[2]
Answer/Explanation
Markscheme
\(2ax\) (A1) (C1)
Note: Award (A1) for \(2ax\). Award (A0) if other terms are seen.
\(2a( – 2) = – 6\) (M1)(M1)
Note: Award (M1) for correct substitution of \(x = – 2\) in their gradient function, (M1) for equating their gradient function to \( – 6\) . Follow through from part (a).
\((a = )1.5\,\,\,\left( {\frac{3}{2}} \right)\) (A1)(ft) (C3)
\({\text{their }}1.5 \times {( – 2)^2} + c = 5\) (M1)
Note: Award (M1) for correct substitution of their \(a\) and point \({\text{A}}\). Follow through from part (b).
\((c = ) – 1\) (A1)(ft) (C2)
Question
The equation of the straight line \({L_1}\) is \(y = 2x – 3.\)
Write down the \(y\)-intercept of \({L_1}\) .[1]
Write down the gradient of \({L_1}\) .[1]
The line \({L_2}\) is parallel to \({L_1}\) and passes through the point \((0,\,\,3)\) .
Write down the equation of \({L_2}\) .[1]
The line \({L_3}\) is perpendicular to \({L_1}\) and passes through the point \(( – 2,\,\,6).\)
Write down the gradient of \({L_3}.\)[1]
Find the equation of \({L_3}\) . Give your answer in the form \(ax + by + d = 0\) , where \(a\) , \(b\) and \(d\) are integers.[2]
Answer/Explanation
Markscheme
\((0,\,\, – 3)\) (A1) (C1)
Note: Accept \( – 3\) or \(y = – 3.\)
\(2\) (A1) (C1)
\(y = 2x + 3\) (A1)(ft) (C1)
Note: Award (A1)(ft) for correct equation. Follow through from part (b)
Award (A0) for \({L_2} = 2x + 3\).
\( – \frac{1}{2}\) (A1)(ft) (C1)
Note: Follow through from part (b).
\(6 = – \frac{1}{2}( – 2) + c\) (M1)
\(c = 5\) (may be implied)
OR
\(y – 6 = – \frac{1}{2}(x + 2)\) (M1)
Note: Award (M1) for correct substitution of their gradient in part (d) and the point \(( – 2,\,\,6)\). Follow through from part (d).
\(x + 2y – 10 = 0\) (or any integer multiple) (A1)(ft) (C2)
Note: Follow through from (d). The answer must be in the form \(ax + by + d = 0\) for the (A1)(ft) to be awarded. Accept any integer multiple.
Question
Consider the function \(f(x) = {x^3} – 3{x^2} + 2x + 2\) . Part of the graph of \(f\) is shown below.
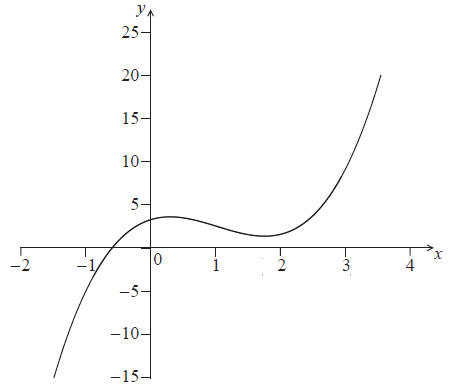
Find \(f'(x)\) .[3]
There are two points at which the gradient of the graph of \(f\) is \(11\). Find the \(x\)-coordinates of these points.[3]
Answer/Explanation
Markscheme
\((f'(x) = )\,\,3{x^2} – 6x + 2\) (A1)(A1)(A1) (C3)
Note: Award (A1) for \(3{x^2}\), (A1) for \( – 6x\) and (A1) for \( + 2\).
Award at most (A1)(A1)(A0) if there are extra terms present.
\(11 = 3{x^2} – 6x + 2\) (M1)
Note: Award (M1) for equating their answer from part (a) to \(11\), this may be implied from \(0 = 3{x^2} – 6x – 9\) .
\((x = )\,\, – 1\,\,,\,\,\,\,(x = )\,\,3\) (A1)(ft)(A1)(ft) (C3)
Note: Follow through from part (a).
If final answer is given as coordinates, award at most (M1)(A0)(A1)(ft) for \(( – 1,\,\, – 4)\) and \((3,\,\,8)\) .
Question
The equation of a curve is \(y = \frac{1}{2}{x^4} – \frac{3}{2}{x^2} + 7\).
The gradient of the tangent to the curve at a point P is \( – 10\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
Find the coordinates of P.[4]
Answer/Explanation
Markscheme
\(2{x^3} – 3x\) (A1)(A1) (C2)
Note: Award (A1) for \(2{x^3}\), award (A1) for \( – 3x\).
Award at most (A1)(A0) if there are any extra terms.[2 marks]
\(2{x^3} – 3x = – 10\) (M1)
Note: Award (M1) for equating their answer to part (a) to \( – 10\).
\(x = – 2\) (A1)(ft)
Note: Follow through from part (a). Award (M0)(A0) for \( – 2\) seen without working.
\(y = \frac{1}{2}{( – 2)^4} – \frac{3}{2}{( – 2)^2} + 7\) (M1)
Note: Award (M1) substituting their \( – 2\) into the original function.
\(y = 9\) (A1)(ft) (C4)
Note: Accept \(( – 2,{\text{ }}9)\).[4 marks]
Question
The equation of line \({L_1}\) is \(y = – \frac{2}{3}x – 2\).
Point P lies on \({L_1}\) and has \(x\)-coordinate \( – 6\).
The line \({L_2}\) is perpendicular to \({L_1}\) and intersects \({L_1}\) when \(x = – 6\).
Write down the gradient of \({L_1}\).[1]
Find the \(y\)-coordinate of P.[2]
Determine the equation of \({L_2}\). Give your answer in the form \(ax + by + d = 0\), where \(a\), \(b\) and \(d\) are integers.[3]
Answer/Explanation
Markscheme
\( – \frac{2}{3}\) (A1) (C1)[1 mark]
\(y = – \frac{2}{3}( – 6) – 2\) (M1)
Note: Award (M1) for correctly substituting \( – 6\) into the formula for \({L_1}\).
\((y = ){\text{ }}2\) (A1) (C2)
Note: Award (A0)(A1) for \(( – 6,{\text{ }}2)\) with or without working.[2 marks]
gradient of \({L_2}\) is \(\frac{3}{2}\) (A1)(ft)
Note: Follow through from part (a).
\(2 = \frac{3}{2}( – 6) + c\)\(\,\,\,\)OR\(\,\,\,\)\(y – 2 = \frac{3}{2}\left( {x – ( – 6)} \right)\) (M1)
Note: Award (M1) for substituting their part (b), their gradient and \( – 6\) into equation of a straight line.
\(3x – 2y + 22 = 0\) (A1)(ft) (C3)
Note: Follow through from parts (a) and (b). Accept any integer multiple.
Award (A1)(M1)(A0) for \(y = \frac{3}{2}x + 11\).[3 marks]
Question
The diagram shows part of the graph of a function \(y = f(x)\). The graph passes through point \({\text{A}}(1,{\text{ }}3)\).
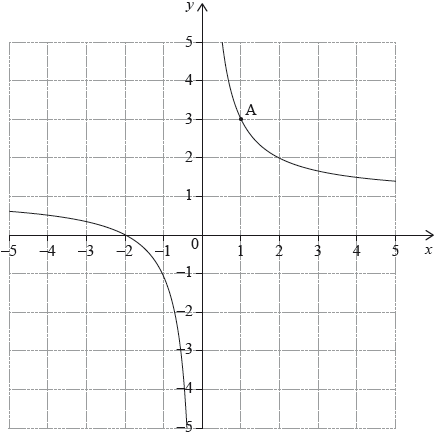
The tangent to the graph of \(y = f(x)\) at A has equation \(y = – 2x + 5\). Let \(N\) be the normal to the graph of \(y = f(x)\) at A.
Write down the value of \(f(1)\).[1]
Find the equation of \(N\). Give your answer in the form \(ax + by + d = 0\) where \(a\), \(b\), \(d \in \mathbb{Z}\).[3]
Draw the line \(N\) on the diagram above.[2]
Answer/Explanation
Markscheme
3 (A1) (C1)
Notes: Accept \(y = 3\)[1 mark]
\(3 = 0.5(1) + c\)\(\,\,\,\)OR\(\,\,\,\)\(y – 3 = 0.5(x – 1)\) (A1)(A1)
Note: Award (A1) for correct gradient, (A1) for correct substitution of \({\text{A}}(1,{\text{ }}3)\) in the equation of line.
\(x – 2y + 5 = 0\) or any integer multiple (A1)(ft) (C3)
Note: Award (A1)(ft) for their equation correctly rearranged in the indicated form.
The candidate’s answer must be an equation for this mark.[3 marks]
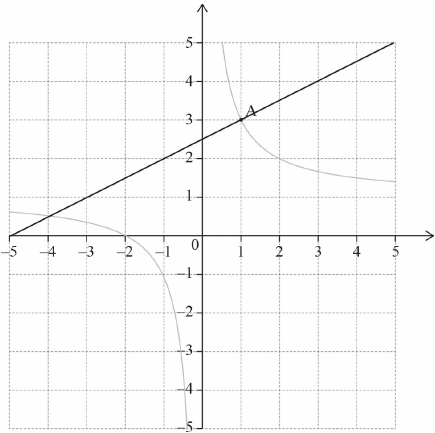(M1)(A1)(ft) (C2)
Note: Award M1) for a straight line, with positive gradient, passing through \((1,{\text{ }}3)\), (A1)(ft) for line (or extension of their line) passing approximately through 2.5 or their intercept with the \(y\)-axis.[2 marks]
Question
The coordinates of point A are \((6,{\text{ }} – 7)\) and the coordinates of point B are \(( – 6,{\text{ }}2)\). Point M is the midpoint of AB.
\({L_1}\) is the line through A and B.
The line \({L_2}\) is perpendicular to \({L_1}\) and passes through M.
Find the coordinates of M.[2]
Find the gradient of \({L_1}\).[2]
Write down the gradient of \({L_2}\).[1]
Write down, in the form \(y = mx + c\), the equation of \({L_2}\).[1]
Answer/Explanation
Markscheme
\((0,{\text{ }}2.5)\)\(\,\,\,\)OR\(\,\,\,\)\(\left( {0,{\text{ }} – \frac{5}{2}} \right)\) (A1)(A1) (C2)
Note: Award (A1) for 0 and (A1) for –2.5 written as a coordinate pair. Award at most (A1)(A0) if brackets are missing. Accept “\(x = 0\) and \(y = – 2.5\)”.[2 marks]
\(\frac{{2 – ( – 7)}}{{ – 6 – 6}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = – \frac{3}{4}{\text{ }}( – 0.75)\) (A1) (C2)[2 marks]
\(\frac{4}{3}{\text{ }}(1.33333 \ldots )\) (A1)(ft) (C1)
Note: Award (A0) for \(\frac{1}{{0.75}}\). Follow through from part (b).[1 mark]
\(y = \frac{4}{3}x – \frac{5}{2}{\text{ }}(y = 1.33 \ldots x – 2.5)\) (A1)(ft) (C1)
Note: Follow through from parts (c)(i) and (a). Award (A0) if final answer is not written in the form \(y = mx + c\).[1 mark]
Question
A function \(f\) is given by \(f(x) = 4{x^3} + \frac{3}{{{x^2}}} – 3,{\text{ }}x \ne 0\).
Write down the derivative of \(f\).[3]
Find the point on the graph of \(f\) at which the gradient of the tangent is equal to 6.[3]
Answer/Explanation
Markscheme
\(12{x^2} – \frac{6}{{{x^3}}}\) or equivalent (A1)(A1)(A1) (C3)
Note: Award (A1) for \(12{x^2}\), (A1) for \( – 6\) and (A1) for \(\frac{1}{{{x^3}}}\) or \({x^{ – 3}}\). Award at most (A1)(A1)(A0) if additional terms seen.[3 marks]
\(12{x^2} – \frac{6}{{{x^3}}} = 6\) (M1)
Note: Award (M1) for equating their derivative to 6.
\((1,{\text{ }}4)\)\(\,\,\,\)OR\(\,\,\,\)\(x = 1,{\text{ }}y = 4\) (A1)(ft)(A1)(ft) (C3)
Note: A frequent wrong answer seen in scripts is \((1,{\text{ }}6)\) for this answer with correct working award (M1)(A0)(A1) and if there is no working award (C1).[3 marks]
Question
The point A has coordinates (4 , −8) and the point B has coordinates (−2 , 4).
The point D has coordinates (−3 , 1).
Write down the coordinates of C, the midpoint of line segment AB.[2]
Find the gradient of the line DC.[2]
Find the equation of the line DC. Write your answer in the form ax + by + d = 0 where a , b and d are integers.[2]
Answer/Explanation
Markscheme
(1, −2) (A1)(A1) (C2)
Note: Award (A1) for 1 and (A1) for −2, seen as a coordinate pair.
Accept x = 1, y = −2. Award (A1)(A0) if x and y coordinates are reversed.[2 marks]
\(\frac{{1 – \left( { – 2} \right)}}{{ – 3 – 1}}\) (M1)
Note: Award (M1) for correct substitution, of their part (a), into gradient formula.
\( = – \frac{3}{4}\,\,\,\left( { – 0.75} \right)\) (A1)(ft) (C2)
Note: Follow through from part (a).[2 marks]
\(y – 1 = – \frac{3}{4}\left( {x + 3} \right)\) OR \(y + 2 = – \frac{3}{4}\left( {x – 1} \right)\) OR \(y = – \frac{3}{4}x – \frac{5}{4}\) (M1)
Note: Award (M1) for correct substitution of their part (b) and a given point.
OR
\(1 = – \frac{3}{4} \times – 3 + c\) OR \( – 2 = – \frac{3}{4} \times 1 + c\) (M1)
Note: Award (M1) for correct substitution of their part (b) and a given point.
\(3x + 4y + 5 = 0\) (accept any integer multiple, including negative multiples) (A1)(ft) (C2)
Note: Follow through from parts (a) and (b). Where the gradient in part (b) is found to be \(\frac{5}{0}\), award at most (M1)(A0) for either \(x = – 3\) or \(x + 3 = 0\).[2 marks]
Question
Consider the function \(f\left( x \right) = \frac{{{x^4}}}{4}\).
Find f’(x)[1]
Find the gradient of the graph of f at \(x = – \frac{1}{2}\).[2]
Find the x-coordinate of the point at which the normal to the graph of f has gradient \({ – \frac{1}{8}}\).[3]
Answer/Explanation
Markscheme
x3 (A1) (C1)
Note: Award (A0) for \(\frac{{4{x^3}}}{4}\) and not simplified to x3.[1 mark]
\({\left( { – \frac{1}{2}} \right)^3}\) (M1)
Note: Award (M1) for correct substitution of \({ – \frac{1}{2}}\) into their derivative.
\({ – \frac{1}{8}}\) (−0.125) (A1)(ft) (C2)
Note: Follow through from their part (a).[2 marks]
x3 = 8 (A1)(M1)
Note: Award (A1) for 8 seen maybe seen as part of an equation y = 8x + c, (M1) for equating their derivative to 8.
(x =) 2 (A1) (C3)
Note: Do not accept (2, 4).[3 marks]
Question
Consider the graph of the function \(y = f(x)\) defined below.
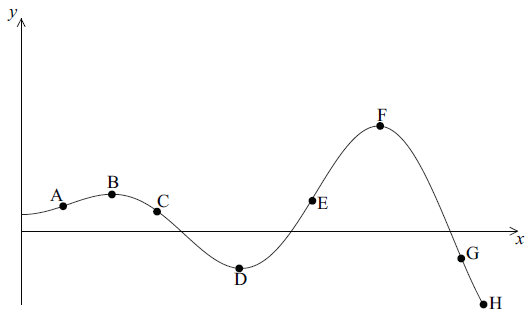
Write down all the labelled points on the curve
that are local maximum points;[1]
where the function attains its least value;[1]
where the function attains its greatest value;[1]
where the gradient of the tangent to the curve is positive;[1]
where \(f(x) > 0\) and \(f'(x) < 0\) .[2]
Answer/Explanation
Markscheme
B, F (C1)
H (C1)
F (C1)
A, E (C1)
C (C2)
Question
Consider the curve \(y = {x^2}\) .
Write down \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[1]
The point \({\text{P}}(3{\text{, }}9)\) lies on the curve \(y = {x^2}\) . Find the gradient of the tangent to the curve at P .[2]
The point \({\text{P}}(3{\text{, }}9)\) lies on the curve \(y = {x^2}\) . Find the equation of the normal to the curve at P . Give your answer in the form \(y = mx + c\) .[3]
Answer/Explanation
Markscheme
\(2x\) (A1) (C1)
\(2 \times 3\) (M1)
\( = 6\) (A1) (C2)
\(m({\text{perp}}) = – \frac{1}{6}\) (A1)(ft)
Note: Follow through from their answer to part (b).
Equation \((y – 9) = – \frac{1}{6}(x – 3)\) (M1)
Note: Award (M1) for correct substitution in any formula for equation of a line.
\(y = – \frac{1}{6}x + 9\frac{1}{2}\) (A1)(ft) (C3)
Note: Follow through from correct substitution of their gradient of the normal.
Note: There are no extra marks awarded for rearranging the equation to the form \(y = mx + c\) .
Question
A sketch of the function \(f(x) = 5{x^3} – 3{x^5} + 1\) is shown for \( – 1.5 \leqslant x \leqslant 1.5\) and \( – 6 \leqslant y \leqslant 6\) .
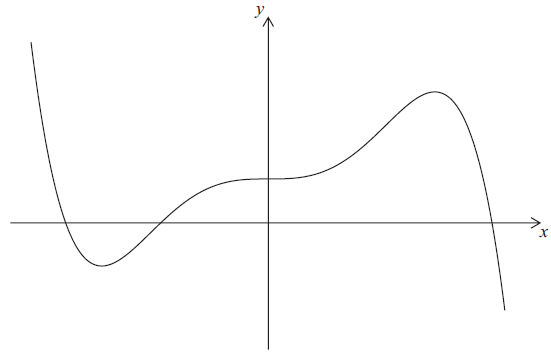
Write down \(f'(x)\) .[2]
Find the equation of the tangent to the graph of \(y = f(x)\) at \((1{\text{, }}3)\) .[2]
Write down the coordinates of the second point where this tangent intersects the graph of \(y = f(x)\) .[2]
Answer/Explanation
Markscheme
\(f'(x) = 15{x^2} – 15{x^4}\) (A1)(A1) (C2)
Note: Award a maximum of (A1)(A0) if extra terms seen.
\(f'(1) = 0\) (M1)
Note: Award (M1) for \(f'(x) = 0\) .
\(y = 3\) (A1)(ft) (C2)
Note: Follow through from their answer to part (a).
\(( – 1.38{\text{, }}3)\) \(( – 1.38481 \ldots {\text{, }}3)\) (A1)(ft)(A1)(ft) (C2)
Note: Follow through from their answer to parts (a) and (b).
Note: Accept \(x = – 1.38\), \(y = 3\) (\(x = – 1.38481 \ldots\) , \(y = 3\)) .