Question
A function is represented by the equation
\[f(x) = a{x^2} + \frac{4}{x} – 3\]
Find \(f ′(x)\) .[3]
The function \(f (x)\) has a local maximum at the point where \(x = −1\).
Find the value of a.[3]
Answer/Explanation
Markscheme
\(f(x) = a{x^2} + 4{x^{ – 1}} – 3\)
\(f'(x) = 2ax – 4{x^{ – 2}}\) (A3)
(A1) for 2ax, (A1) for –4x –2 and (A1) for derivative of –3 being zero. (C3)[3 marks]
\(2ax – 4x^{-2} = 0\) (M1)
\(2a( – 1) – 4{( – 1)^{ – 2}} = 0\) (M1)
\( -2a – 4 = 0\)
\(a = -2\) (A1)(ft)
(M1) for setting derivative function equal to 0. (M1) for inserting \(x = -1\) but do not award (M0)(M1) (C3)[3 marks]
Question
Let \(f (x) = 2x^2 + x – 6\)
Find \(f'(x)\).[3]
Find the value of \(f'( – 3)\).[1]
Find the value of \(x\) for which \(f'(x) = 0\).[2]
Answer/Explanation
Markscheme
\(f'(x) = 4x + 1\) (A1)(A1)(A1) (C3)
Note: Award (A1) for each term differentiated correctly.
Award at most (A1)(A1)(A0) if any extra terms seen.[3 marks]
\(f'( – 3) = – 11\) (A1)(ft) (C1)[1 mark]
\(4x + 1 = 0\) (M1)
\(x = – \frac{{1}}{{4}}\) (A1)(ft) (C2)[2 marks]
Question
The table given below describes the behaviour of f ′(x), the derivative function of f (x), in the domain −4 < x < 2.
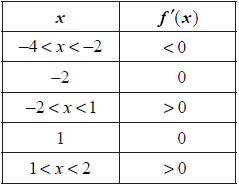
State whether f (0) is greater than, less than or equal to f (−2). Give a reason for your answer.[2]
The point P(−2, 3) lies on the graph of f (x).
Write down the equation of the tangent to the graph of f (x) at the point P.[2]
The point P(−2, 3) lies on the graph of f (x).
From the information given about f ′(x), state whether the point (−2, 3) is a maximum, a minimum or neither. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
greater than (A1)
Gradient between x = −2 and x = 0 is positive. (R1)
OR
The function is increased between these points or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
y = 3 (A1)(A1) (C2)
Note: Award (A1) for y = a constant, (A1) for 3.[2 marks]
minimum (A1)
Gradient is negative to the left and positive to the right or equivalent. (R1) (C2)
Note: Accept a sketch. Do not award (A1)(R0).[2 marks]
Question
f (x) = 5x3 − 4x2 + x
Find f‘(x).[3]
Find using your answer to part (a) the x-coordinate of
(i) the local maximum point;
(ii) the local minimum point.[3]
Answer/Explanation
Markscheme
15x2 – 8x + 1 (A1)(A1)(A1) (C3)
Note: Award (A1) for each correct term.[3 marks]
15x2 – 8x +1 = 0 (A1)(ft)
Note: Award (A1)(ft) for setting their derivative to zero.
(i) \((x =)\frac{1}{5}(0.2)\) (A1)(ft)
(ii) \((x =)\frac{1}{3}(0.333)\) (A1)(ft) (C3)
Notes: Follow through from their answer to part (a).[3 marks]
Question
Consider the function \(f (x) = ax^3 − 3x + 5\), where \(a \ne 0\).
Find \(f ‘ (x) \).[2]
Write down the value of \(f ′(0)\).[1]
The function has a local maximum at x = −2.
Calculate the value of a.[3]
Answer/Explanation
Markscheme
\( f ‘(x) = 3ax^2 – 3\) (A1)(A1) (C2)
Note: Award a maximum of (A1)(A0) if any extra terms are seen.
−3 (A1)(ft) (C1)
Note: Follow through from their part (a).
\(f ‘(x) = 0\) (M1)
Note: This may be implied from line below.
\(3a(-2)^2 – 3 = 0\) (M1)
\((a =) \frac{1}{4}\) (A1)(ft) (C3)
Note: Follow through from their part (a).
Question
Expand the expression \(x(2{x^3} – 1)\).[2]
Differentiate \(f(x) = x(2{x^3} – 1)\).[2]
Find the \(x\)-coordinate of the local minimum of the curve \(y = f(x)\).[2]
Answer/Explanation
Markscheme
\(2{x^4} – x\) (A1)(A1) (C2)
Note: Award (A1) for \(2{x^4}\), (A1) for \( – x\).[2 marks]
\(8{x^3} – 1\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for \(8{x^3}\), (A1)(ft) for \(–1\). Follow through from their part (a).
Award at most (A1)(A0) if extra terms are seen.[2 marks]
\(8{x^3} – 1 = 0\) (M1)
Note: Award (M1) for equating their part (b) to zero.
\((x = )\frac{1}{2}{\text{ (0.5)}}\) (A1)(ft) (C2)
Notes: Follow through from part (b).
\(0.499\) is the answer from the use of trace on the GDC; award (A0)(A0).
For an answer of \((0.5, –0.375)\), award (M1)(A0).[2 marks]
Question
Consider the curve \(y = {x^3} + kx\).
Write down \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[1]
The curve has a local minimum at the point where \(x = 2\).
Find the value of \(k\).[3]
The curve has a local minimum at the point where \(x = 2\).
Find the value of \(y\) at this local minimum.[2]
Answer/Explanation
Markscheme
\(3{x^2} + k\) (A1) (C1)[1 mark]
\(3{(2)^2} + k = 0\) (A1)(ft)(M1)
Note: Award (A1)(ft) for substituting 2 in their \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\), (M1) for setting their \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\).
\(k = – 12\) (A1)(ft) (C3)
Note: Follow through from their derivative in part (a).[3 marks]
\({2^3} – 12 \times 2\) (M1)
Note: Award (M1) for substituting 2 and their –12 into equation of the curve.
\( = – 16\) (A1)(ft) (C12)
Note: Follow through from their value of \(k\) found in part (b).[2 marks]
Question
Consider the graph of the function \(f(x) = {x^3} + 2{x^2} – 5\).
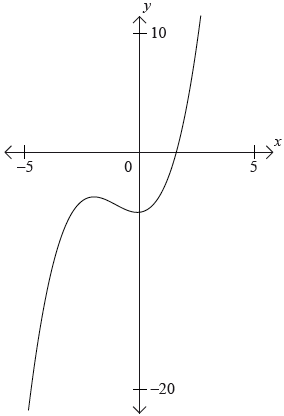
Label the local maximum as \({\text{A}}\) on the graph.[1]
Label the local minimum as B on the graph.[1]
Write down the interval where \(f'(x) < 0\).[1]
Draw the tangent to the curve at \(x = 1\) on the graph.[1]
Write down the equation of the tangent at \(x = 1\).[2]
Answer/Explanation
Markscheme
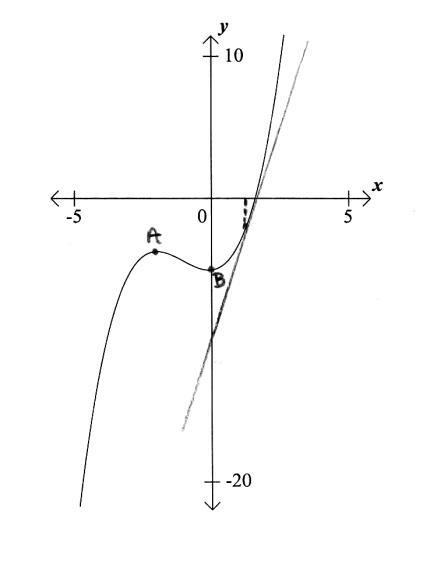
correct label on graph (A1) (C1)[1 mark]
correct label on graph (A1) (C1)[1 mark]
\( – 1.33 < x < 0\) \(\left( { – \frac{4}{3} < x < 0} \right)\) (A1) (C1)[1 mark]
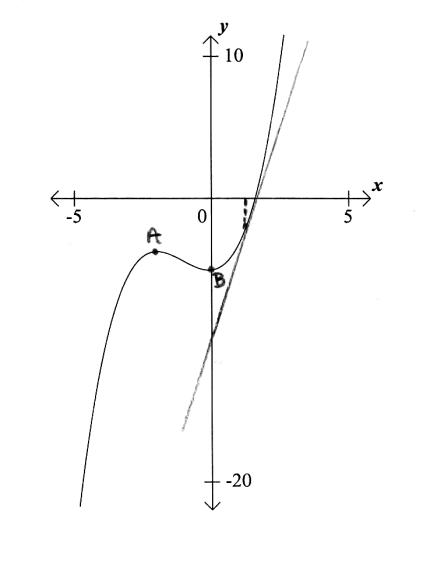
tangent drawn at \(x = 1\) on graph (A1) (C1)[1 mark]
\(y = 7x – 9\) (A1)(A1) (C2)
Notes: Award (A1) for \(7\), (A1) for \(-9\).
If answer not given as an equation award at most (A1)(A0).[2 marks]
Question
A function is given as \(f(x) = 2{x^3} – 5x + \frac{4}{x} + 3,{\text{ }} – 5 \leqslant x \leqslant 10,{\text{ }}x \ne 0\).
Write down the derivative of the function.[4]
Use your graphic display calculator to find the coordinates of the local minimum point of \(f(x)\) in the given domain.[2]
Answer/Explanation
Markscheme
\(6{x^2} – 5 – \frac{4}{{{x^2}}}\) (A1)(A1)(A1)(A1) (C4)
Note: Award (A1) for \(6{x^2}\), (A1) for \(–5\), (A1) for \(–4\), (A1) for \({x^{ – 2}}\) or \(\frac{1}{{{x^2}}}\).
Award at most (A1)(A1)(A1)(A0) if additional terms are seen.[4 marks]
\((1.15,{\text{ }} 3.77)\) \(\left( {{\text{(1.15469…, 3.76980…)}}} \right)\) (A1)(A1) (C2)
Notes: Award (A1)(A1) for “\(x = 1.15\) and \(y = 3.77\)”.
Award at most (A0)(A1)(ft) if parentheses are omitted.[2 marks]
Question
A cuboid has a rectangular base of width \(x\) cm and length 2\(x\) cm . The height of the cuboid is \(h\) cm . The total length of the edges of the cuboid is \(72\) cm.
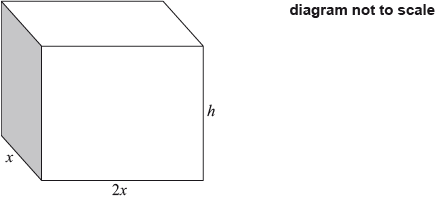
The volume, \(V\), of the cuboid can be expressed as \(V = a{x^2} – 6{x^3}\).
Find the value of \(a\).[3]
Find the value of \(x\) that makes the volume a maximum.[3]
Answer/Explanation
Markscheme
\(72 = 12x + 4h\;\;\;\)(or equivalent) (M1)
Note: Award (M1) for a correct equation obtained from the total length of the edges.
\(V = 2{x^2}(18 – 3x)\) (A1)
\((a = ){\text{ }}36\) (A1) (C3)
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 72x – 18{x^2}\) (A1)
\(72x – 18{x^2} = 0\;\;\;\)OR\(\;\;\;\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) (M1)
Notes: Award (A1) for \( – 18{x^2}\) seen. Award (M1) for equating derivative to zero.
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Note: Follow through from part (a).
OR
Sketch of \(V\) with visible maximum (M1)
Sketch with \(x \geqslant 0,{\text{ }}V \geqslant 0\) and indication of maximum (e.g. coordinates) (A1)(ft)
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Notes: Follow through from part (a).
Award (M1)(A1)(A0) for \((4,{\text{ }}192)\).
Award (C3) for \(x = 4,{\text{ }}y = 192\).
Question
A quadratic function \(f\) is given by \(f(x) = a{x^2} + bx + c\). The points \((0,{\text{ }}5)\) and \(( – 4,{\text{ }}5)\) lie on the graph of \(y = f(x)\).
The \(y\)-coordinate of the minimum of the graph is 3.
Find the equation of the axis of symmetry of the graph of \(y = f(x)\).[2]
Write down the value of \(c\).[1]
Find the value of \(a\) and of \(b\).[3]
Answer/Explanation
Markscheme
\(x = – 2\) (A1)(A1) (C2)
Note: Award (A1) for \(x = \) (a constant) and (A1) for \( – 2\).[2 marks]
\((c = ){\text{ }}5\) (A1) (C1)[1 mark]
\( – \frac{b}{{2a}} = – 2\)
\(a{( – 2)^2} – 2b + 5 = 3\) or equivalent
\(a{( – 4)^2} – 4b + 5 = 5\) or equivalent
\(2a( – 2) + b = 0\) or equivalent (M1)
Note: Award (M1) for two of the above equations.
\(a = 0.5\) (A1)(ft)
\(b = 2\) (A1)(ft) (C3)
Note: Award at most (M1)(A1)(ft)(A0) if the answers are reversed.
Follow through from parts (a) and (b).[3 marks]
Question
A factory produces shirts. The cost, C, in Fijian dollars (FJD), of producing x shirts can be modelled by
C(x) = (x − 75)2 + 100.
The cost of production should not exceed 500 FJD. To do this the factory needs to produce at least 55 shirts and at most s shirts.
Find the cost of producing 70 shirts.[2]
Find the value of s.[2]
Find the number of shirts produced when the cost of production is lowest.[2]
Answer/Explanation
Answer/Explanation
Markscheme
(70 − 75)2 + 100 (M1)
Note: Award (M1) for substituting in x = 70.
125 (A1) (C2)[2 marks]
(s − 75)2 + 100 = 500 (M1)
Note: Award (M1) for equating C(x) to 500. Accept an inequality instead of =.
OR
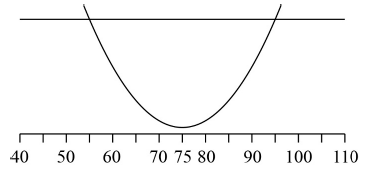 (M1)
(M1)
Note: Award (M1) for sketching correct graph(s).
(s =) 95 (A1) (C2)[2 marks]
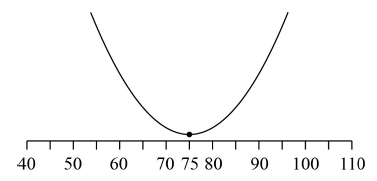 (M1)
(M1)
Note: Award (M1) for an attempt at finding the minimum point using graph.
OR
\(\frac{{95 + 55}}{2}\) (M1)
Note: Award (M1) for attempting to find the mid-point between their part (b) and 55.
OR
(C’(x) =) 2x − 150 = 0 (M1)
Note: Award (M1) for an attempt at differentiation that is correctly equated to zero.
75 (A1) (C2)[2 marks]
Question
Consider the graph of the function \(y = f(x)\) defined below.
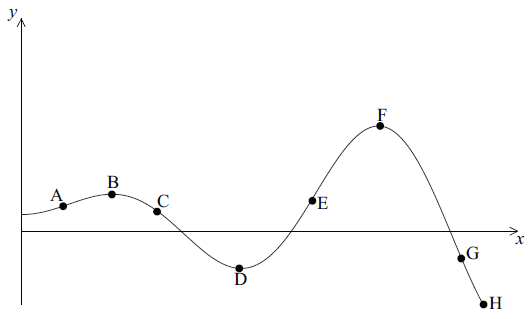
Write down all the labelled points on the curve
that are local maximum points;[1]
where the function attains its least value;[1]
where the function attains its greatest value;[1]
where the gradient of the tangent to the curve is positive;[1]
where \(f(x) > 0\) and \(f'(x) < 0\) .[2]
Answer/Explanation
Markscheme
B, F (C1)
H (C1)
F (C1)
A, E (C1)
C (C2)
Question
A small manufacturing company makes and sells \(x\) machines each month. The monthly cost \(C\) , in dollars, of making \(x\) machines is given by
\[C(x) = 2600 + 0.4{x^2}{\text{.}}\]The monthly income \(I\) , in dollars, obtained by selling \(x\) machines is given by
\[I(x) = 150x – 0.6{x^2}{\text{.}}\]\(P(x)\) is the monthly profit obtained by selling \(x\) machines.
Find \(P(x)\) .[2]
Find the number of machines that should be made and sold each month to maximize \(P(x)\) .[2]
Use your answer to part (b) to find the selling price of each machine in order to maximize \(P(x)\) .[2]
Answer/Explanation
Markscheme
\(P(x) = I(x) – C(x)\) (M1)
\( = – {x^2} + 150x – 2600\) (A1) (C2)
\( – 2x + 150 = 0\) (M1)
Note: Award (M1) for setting \(P'(x) = 0\) .
OR
Award (M1) for sketch of \(P(x)\) and maximum point identified. (M1)
\(x = 75\) (A1)(ft) (C2)
Note: Follow through from their answer to part (a).
\(\frac{{7875}}{{75}}\) (M1)
Note: Award (M1) for \(7875\) seen.
\( = 105\) (A1)(ft) (C2)
Note: Follow through from their answer to part (b).

